All published articles of this journal are available on ScienceDirect.
Speed Limits and Pavement Friction: A Theoretical and Experimental Study
Abstract
Background:
As is well known, in road construction, quality acceptance procedures and quality assurance/control procedures during operations (for maintenance and rehabilitation purposes) focus on material quality from a mechanistic and safety perspective. This latter usually entails the consideration of friction and surface texture indicators. When friction requirements (e.g., side friction coefficients measured through the SCRIM machine) are not satisfied, road agencies have two main options: closing the traffic or having lower speed limits. The first option is often unrealistic and challenging. It turns out that a new, often temporary, speed limit is required and appropriate methodologies are required to carry out this critical task.
Aims and Objectives:
Consequently, the objective of the study presented in this paper is to set up a methodology aiming at engineering-based assessments of speed limits based on actual friction values. Original and consistent algorithms are set up to solve theoretical and practical issues.
Result and Conclusion:
The main contributions of this study include: (1) setting up a methodology for friction-based assessment of speed limits through innovative speed-friction relationships and criteria; (2) utilising the methodology for a case study; (3) providing recommendations for the application.
Results prove that the algorithms set up are reasonable and well-grounded in logic. They can benefit both researchers and practitioners.
1. BACKGROUND
Road intrinsic safety and speed limits build on well-known parameters (e.g., curvature change ratio [1-3]), less known parameters (e.g., behaviour, manouvers, etc.), and policy-based factors. By referring to this last option, for example, posted speed limits may derive from operating speeds based on local policy-based parameters and different methods are available for practitioners to make informed decisions in a given jurisdiction (see, for example [4-6]. This implies that diverse theories and systems have been set up and can be used in practice: an engineering approach, expert systems, optimization, and injury minimization [6, 7]. Furthermore, as a matter of fact, the posted speed limit interacts with operating speeds, and it should be treated as an exogenous variable in models of operating speed [8].
As is well known, the engineering approach includes two possible approaches: operating Speed Method and road risk method. This latter builds on measurements and data related to the actual state of a pavement because accident risk depends on pavement-tyre interaction. To this end, quality acceptance and quality assurance/control procedures during operations (for maintenance and rehabilitation purposes) focus on material quality from a mechanistic and safety perspective [9] and provide the needed data. Consequently, when friction requirements are not satisfied (e.g., side friction coefficients measured through the SCRIM machine [10-12],), road agencies have two main options to reduce the risk: closing the traffic or lowering speed limits. The first option is often unrealistic and hard to follow and put into practice. It turns out that a new, often temporary, speed limit is necessary and methodologies are required to carry out such a difficult task. Indeed, setting up a new speed limit based on the actual conditions of a pavement is challenging, because many boundary conditions, parameters, and corresponding standards/devices affect friction values, e.g., speed, direction, slip, tire, lubricated or dry conditions, and pavement surface properties [13, 14]. In more detail: i) 100%-slip versus peak friction are very different and their relationship depends on many factors [15, 16]; ii) there are many correlations among results obtained through different devices [17-23]. This notwithstanding results are not always complying and the dependency on texture properties [24, 25] increases the complexity of the problem; iii) friction depends on speed [26, 27]. This dependency appears to be affected by a number of factors. Furthermore, values indicated in standards are usually not consistent with the ones derived from real experiments; iv) even if skid resistance depends on water film thickness, the minimum skid resistance threshold for safe wet-weather driving is usually specified by based on either engineering judgement or past experience. To this end, advanced models have been set up to predict skid resistance as a function of water film thickness [28].
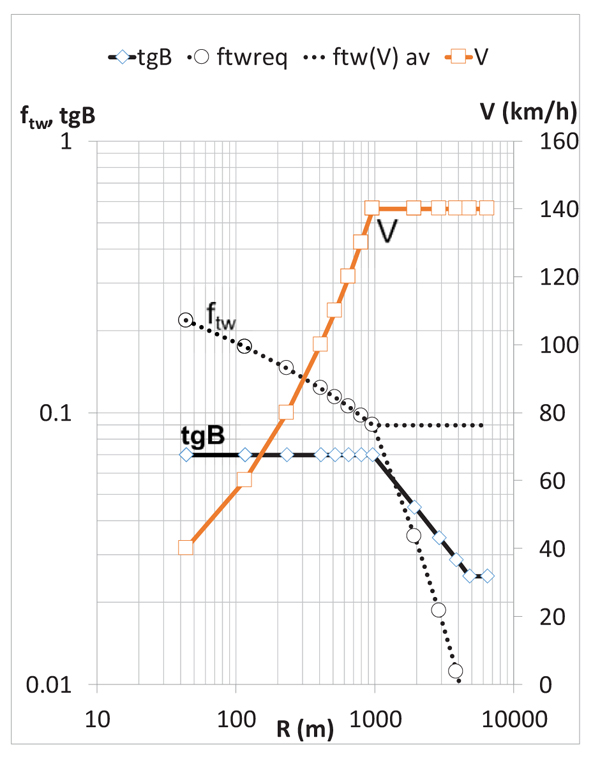
In practice, standards usually build on the following (see for example the ministerial decree DM 6792/01, in Italy). For values of radii lower than a given threshold, the ideal transverse friction is provided by the standard. (e.g., ftw(V), wet conditions). As a consequence, the well-known equation for the steering stability in curve is used to derive the radius (R), as a function of speed (V), transverse slope (e.g., 7%), and transverse friction (ftw(V)=ftwreq, i.e., ft required in wet conditions, cf. Fig. (1), left part with R≤R*=964):
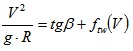 |
(1) |
For very high radii (let us say R+>R*, but with R<5R*), standards usually allow reducing the banking according to a linear relationship (in the bi-logarithmic plane), the speed being constrained to a given maximum value (e.g., V=140km/h):
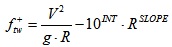 |
(2) |
Where SLOPE and INT are the slope and the intercept that the standard sets up (e.g., -0.64 and 0.75, respectively). This fact implies that, for R>R*, the corresponding transverse friction required (let us indicate it with ftw+) is lower than the transverse friction available (this latter is termed ftav in Fig. (1)). Importantly, for R<R*, friction required and friction “available” (as per standard) are the same (Fig. 1).
By referring to both dry and wet conditions, it seems relevant to point out that there is a certain discrepancy between the friction coefficients that can be estimated through the real, experimental data and the ones which are reported in the standards and national regulations. Indeed, national regulations are precautionary and when real data are considered [29, 30] the following applies:
- Even if it is confirmed that the pick friction coefficient (slip=0.1-0.2) is higher than the locked -wheel value, the impact of the car speed on the pick coefficient is usually only about 0.2 (e.g., increasing the speed from 50 to 110km/h there is a reduction of 0.2) and depends on the (lubricated/dry) state of tire-pavement interface.
- Experimental braking distances [29] imply friction coefficients which decrease over speed of just one tenth of the corresponding regulation-based values. Variations result around 0.01 (from 120km/h to 40) for real data, and quite different from 0.1-0.2 (as per the abovementioned national regulations).
- Consequently, the first derivative of friction coefficients with respect to speed (m/s) is about 0.001s/m, for real data and about 0.01s/m for regulation-based data (in the domain 50-110 km/h).
Apart from the complexity of friction phenomena, note that stopping distance depends on a number of factors besides friction [31]. For example, reaction times (thinking time) can vary from 1.2 up to 1.5 s [32] and the initial speed is the most sensitive factor to stopping distances of vehicles based on the results of sensitivity analyses carried out by [33].
In summarising the principles, philosophies, and procedures for deriving speed limits may greatly vary and this complexity still remains when considering the consequences of friction-related nonconformities on safety and speed limits.
2. OBJECTIVES
Based on the above, the objectives of this study are to set up a physical-based method for the derivation of speed limits based on friction data. The remaining parts of the paper are organised as follows. The next section deals with modelling. Algorithms and modelling are then applied to a case-study. Conclusions and references follow the application.
3. MODELLING
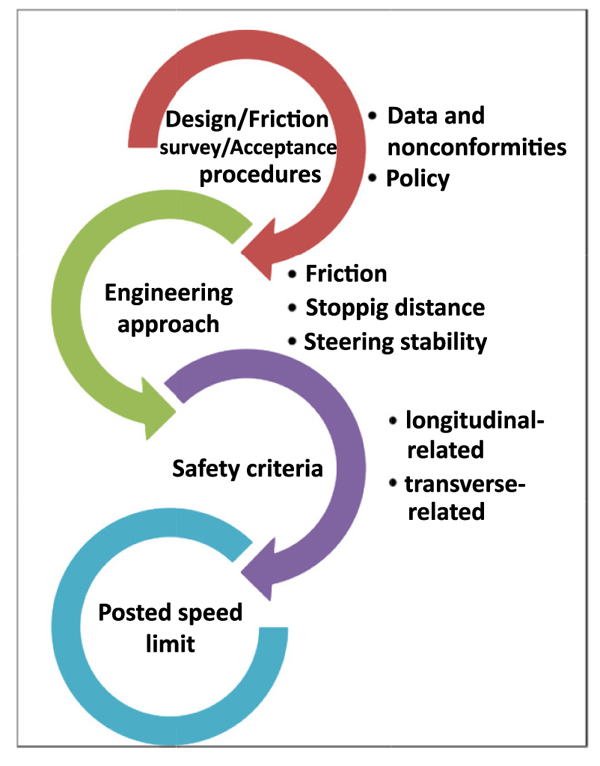
The method herein set up aims at providing a tool for posted speed limits based on safety instances. It includes: i) deriving physical parameters based on experimental data (phase 1); ii) modelling how the physical parameters vary as a function of speed in wet conditions (phases 2 and 3); iv) deriving the corresponding variations in dry conditions (phase 4); v) applying physical laws in order to derive the new speed limit that is required in order to have a lower or equal risk to the design one even with the reduced friction. Phases are illustrated below (Fig. 2).
Phase 1: In this phase, the data available (friction, FRS2, and surface texture of the pavement, Tx) are transformed into the physical parameters needed. For example, FRS2 may be the Side Friction Coefficient, SFC, percent slip of 34%, yaw angle of 20 degrees, BS 7941-1:2006, 60 km/h and, through equation (3), the values of FRS1 are derived (where FRS1 is, for example, the friction coefficient with a fixed slip of 20%, wet conditions, speed of 60km/h). This phase is carried out through equations 3 and 4, based on the literature [17].
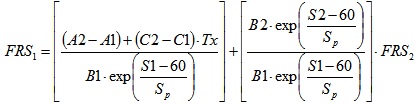 |
(3) |
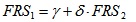 |
(4) |
Note that the coefficients Ai, Bi, Ci and Si, depend on the couple of devices (e.g., SCRIM-SFC and SKIDDOMETER), while Sp (speed constant) depends on macrotexture data and device, and S1, S2 are the Slip Velocities of 1 and 2, respectively, and depend on the conditions in which FRS1 and FRS2 are measured. For example, if FRS2=SFC, then FRS1 is intended to approximate the total, T, horizontal force available in pavement-tyre interface, in wet conditions, w, at 60km/h, fTw(60).
Phase 2: This phase focuses on the dependency on the speed of tangential (l) and total (T) friction. From fTw(60) (where T stands for total, 60 for 60 km/h, and w for wet), the curves of fTw(V) and flw(V), i.e., total and tangential friction, respectively, for a given speed V, in wet conditions, are derived. In this phase, equations 5 and 6 are used. The coefficients of these equations should build on national regulations, because of the legal implications.
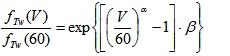 |
(5) |
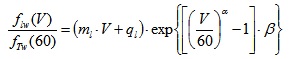 |
(6) |
Note that fTw(V) refers to the total horizontal friction in wet conditions, for a speed of V, while flw(V) refers to the longitudinal friction in wet conditions. Furthermore, α and β are coefficients to calibrate that allow better tuning the first derivative among the different points of the curve. The coefficients ml and ql aim at governing the vectorial addition of longitudinal and transverse friction. For example, if fTw(60) 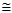 0.4, β
0.4, β 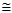 -2.37, α
-2.37, α 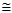 0.19,m
0.19,m 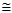 0003,q
0003,q 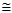 0.9345, it follows that flw(25)
0.9345, it follows that flw(25) 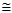 0.55, flw(60)
0.55, flw(60) 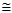 0.39, and flw(140)
0.39, and flw(140) 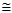 0.26.
0.26.
Phase 3: This phase addresses the transverse (t) friction in wet conditions, ftw(V). Based on V and on flw(v), ftw(v) is derived. In this phase, equation 7 is used. Note that ftw(V) affects the equation of stability in a curve and more precisely the percentage of the centrifugal force that is balanced by the transverse slope. Note that the rationale behind ftw(V) is that in tyre-pavement interface there is an upper limit for the friction force (which combines longitudinal and radial components). Consequently, the higher flw(v) is, the lower ftw(V) must be. In other words, just a small percentage of the total available interface friction is “reserved” to ft, the vectorial sum being fTw(V) (cf. Eq.8):
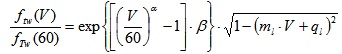 |
(7) |
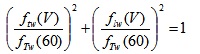 |
(8) |
Phase 4: This phase addresses the friction in dry conditions (d). Based on fTw(60), also fTd(60) (where d refers to dry and T to total) is derived. This phase is carried out through the use of a proportionality coefficient based on regulations (if present) or real data (e.g., [29]). More in general, this process is used also for deriving fld(V), longitudinal friction course, dry conditions, and ftd (V):
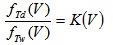 |
(9) |
Consequently, it follows:
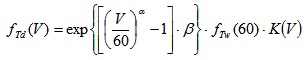 |
(10) |
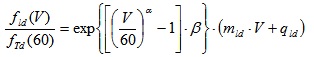 |
(11) |
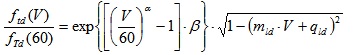 |
(12) |
The rationale behind the equations above (5 to 12) builds on the following:
- Quadratics (first derivative negative; second derivative positive) or linear relationships may well approximate both real values and standard values for given (narrow) ranges. Unfortunately, they do not represent properly, neither the reduction of friction with speed (for a number of causes, e.g., because of the change of the first derivative after the minimum for quadratics) nor the vectorial instances (t2+l2=T2, cf. eq. 8);
- The exponential function set up above permits having a given, finite value (Total percentage, cf. equation 5) when the speed approaches 0, i.e., e-β, where β is negative;
- At the same time at 60 km/h, the same percentage tends to 1 (cf. equation 5);
- And finally, when V tends to infinity, the percentage above tends to zero. This synergistically happens to all the related quantities (i.e., flw(V), ftw(V), fTd(V), fld(V), ftd(V), cf. equations 6, 7, 10, 11, and 12, respectively);
- α allows easily tuning the impact of V, without affecting what happens in the “fixed points” above (i.e., V=0, 60, →∞), included the only one that originates from real data (usually at 60km/h);
- α, β, q, m are estimated based on real data and regulations (e.g., dry conditions [29],). For example, if data from [29] were used, in first approximation, it would result k=1.4-1.5, mlw=mld=0, qlw=qld=95%;
- The choice of 60 is purely and simply conventional. 60 is just the hypothetical speed at which data are gathered (experimental points).
- National regulations have usually two sets of values: upper curve (for motorways) and lower curve (for secondary roads); when needed, equations may follow the pertaining set of values (calibration).
Phase 5: In this phase, we impose the Same-stopping Distance (SD) condition as a potential criterion for having the same risk despite the reduced friction. The criterion one is as follows:
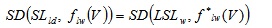 |
(13) |
where SD is the stopping distance (thinking + braking, DA), SL is the speed limit (unknown), flw(V) is the corresponding tangential friction coefficient, LSL is the legal speed limit, f*lw(V) is the “legal”, longitudinal friction coefficient. In other words, in the equation above, the stopping distance is derived in terms of actual surface characteristics (left hand of equation 13), or as per the design standard/state-of-the-art (right hand of equation 13). For example, if the LSL is 110km/h and the corresponding SD is about 150m, while the corresponding f*lw(60) is about 0.5, this implies that the stopping distance must be still 150meters (even if the friction is lower than 0.5), and this goal is achieved through an SL lower than LSL. The following algorithm for the derivation of the thinking (D1), and braking (D2) distance can be used (see for example the Italian Decree DM 6792/01):
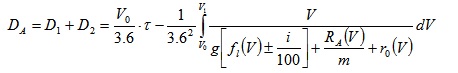 |
(14) |
Where SD=DA is the stopping distance (m), D1 is the thinking distance (m), D2 is the braking distance (m), τ is the reaction time (s), V0 is the initial speed, V1 is the final speed (e.g., 0), g=9.81m/s2, fl(V) is the tangential friction coefficient, i is the slope, RA (V) is the aerodynamic resistance (N), m refers to car mass (kg), and r0 refers to the rolling resistance (supposed as negligible). The following are given:
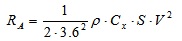 |
(15) |
And
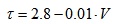 |
(16) |
Where ρ is the air density (1.15kg/m3), S is the resistant surface (2.1m2), Cx is the aerodynamic coefficient (0.35), V is the car speed (km/h).
It is noted that the application of this criterion mostly builds on wet, longitudinal friction.
Phase 6: Application of criterion two (stopping distance in dry conditions). This criterion follows the framework above but refers to dry conditions (and not wet):
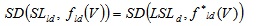 |
(17) |
Phase 7: In this phase we impose the same-surplus of transverse friction (Δ) condition as a potential criterion for having the same risk despite the reduced friction. Indeed, the steering stability of a vehicle approaching a curve is among the most important part of vehicle handling and stability [34]. For high radii R, given transverse slope, ideal conditions of friction, at the LSL, there is usually a “safety factor”, Δ, because the LSL is lower than the design speed (cf. equations 18 and 19). This safety condition must be still present also when friction is lower and the SL is lower. This criterion reads as follows:
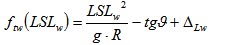 |
(18) |
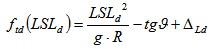 |
(19) |
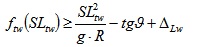 |
(20) |
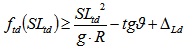 |
(21) |
Where LSDw and LSLd are the legal speed limits in wet/dry conditions, respectively (e.g., 110 and 130km/h), g is the gravity acceleration, R is the horizontal radius, tg θ is the banking of the circular track (banking or transverse slope), ΔLw and ΔLd refer to the friction surplus in legal conditions (the ones stated or implicitly assumed in the standards). In contrast, SLtw and SLtd are the corresponding speed limits in real conditions of friction, based on this criterion. They are the “reduced” speed limits (lower than the legal speed limits) that originate from having an actual friction that is lower than the scheduled/legal friction.
Phase 8: In this phase, based on the speed limits derived for the different criteria, minima are derived. Based on the abovementioned SD criterion (stopping distance) and the Δ criterion (steering stability) four-speed limits originate as per the equations above. Finally, this phase addresses the derivation of the new speed limit in wet conditions and the new speed limit in dry conditions.
Based on the above, it results:
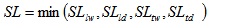 |
(22) |
Alternatively, this phase may be split as follows:
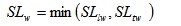 |
(23) |
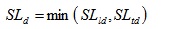 |
(24) |
Note that equations 1-4, 14-16 are based on the literature. In contrast, the remaining equations (5-13, 17-23) are new and original.
4. APPLICATION TO A CASE-STUDY
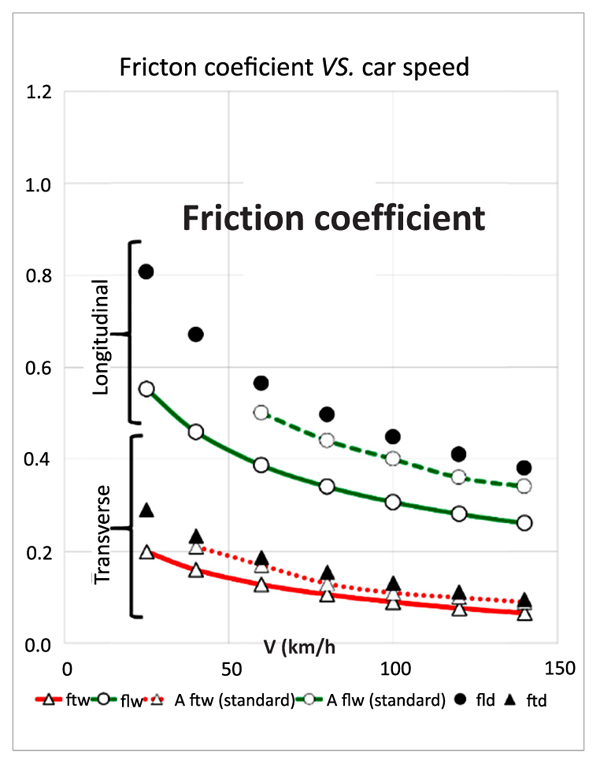
The model set up above was applied to a case-study (rural road located in southern Italy), in which pavement high-speed monitoring pointed out a condition of unsatisfactory pavement friction. Friction values were measured at 60km/h (SFC, BS 7941-1:2006) and surface texture was measured in terms of sand patch method (EN 13036-1:2002). Data were treated through the algorithms above in order to derive friction variations as a function of car speeds. The differences between the as-design scenario (friction values complying with standards and requirements) and the actual conditions of the pavement (as-built) are depicted in Fig. (3). Six trends are represented. Four of them refer to the actual conditions: transverse wet (ftw, solid line), transverse dry (ftd, without line), longitudinal wet (flw, solid line), longitudinal dry (fld, without line). The remaining two trends refer to the standards (A ftw standard and Aflw standard, dotted lines). Values in Fig. (3) point out that the actual friction (as-built pavement) is lower than the required one (as-design friction) and this calls for the reduction of the speed limit.
While Fig. (3) derives from the application of equations 3 to 12, the discussions below summarise the application of the method to derive the speed limits based on the necessity to have a stopping distance lower than the one corresponding to the specifications (equations 13 to 17) and based on the compliance with the criterion 2 (steering stability, equations 18 to 21).
Based on national regulations, in the ideal case (as-design), in wet conditions, the SFC is 53 and the speed limit is 110km/h (while in dry conditions the speed limit is 130 km/h). Based on the abovementioned formula, at 110km/h, in wet conditions, the braking distance, D2, is 100.2m, the thinking time, τ, is 1.7s, the thinking distance, D1, is 51.9m, and the stopping distance, DA=D1+D2, is about 150m (Figure 5.1.2.b, page 52, DM 6792/01).
Being the actual value of SFC (40) lower than the design value (e.g., 53), a lower speed limit is required in order to assure the same (or a lower) stopping distance (i.e., ≤150m). Using eq.14 with the given algorithms for friction, at about 100km/h, in wet conditions, the stopping distance, DA=D1+D2, is about 150m, which complies with the one assumed in terms of design. In other words, based on the criterion of the “conservation” of the stopping distance in wet conditions, the new speed limit might be 100km/h.
By referring to the as-design pavement in dry conditions, at 130km/h (posted speed in dry and ideal conditions), based on dry tangential friction, the stopping distance results about 155 m (equations, 9, 11, and 14).
Being the actual value of SFC (e.g., 40) lower than the design value (e.g., 53), also in dry conditions, a lower value of fld is expected. Using eq.1 4, in dry conditions, at about 100km/h, the stopping distance is about 120 m (<150m).
In summarising, based on the first criterion, a posted speed of 100km/h would assure a stopping distance always lower than (or equal to) the one stated for the as-design friction.
By referring to the steering stability, in order to apply this criterion (equations 18 to 21), in wet conditions, the reference speed to consider is now 110km/h (ideal posted speed). By referring to a given curve radius (800m), the following observations apply. Let the design speeds be 90-140km/h (motorway, page 21, DM 6792/01). Under ideal-but-wet conditions, at 110km/h, being 110 lower than 140 (Fig. 1): i) the transverse slope is 0.07; ii) the radial friction (wet conditions) is about 0.11, which complies with the regulation (DM 6792/01, page 60); iii) the corresponding minimum radius can be derived based on equation (V2/gR=ft+tgB), and is about 547m. This implies that for radii, R+, higher than the above-mentioned value (e.g., 800m), there will be a certain “safety margin”, given by 0.11-(V2·g-1·R-1-0.07). For example, if R=800m, this implies a safety margin of about 0.06.
As abovementioned, in wet conditions, the speed limit is 110km/h (as-design). In contrast, in the as-built conditions, based on the application of the 1st criterion, it mustn’t be higher than 100km/h. Under wet conditions, at 100km/h, being 100 lower than 140 (cf. Fig. 1: i) the transverse slope is 0.07; ii) the radial friction (wet conditions) is about 0.09; iii) the corresponding minimum radius can be derived based on equation (V2/gR=ft+tgB), and is about 547m. This implies that for radii, R+, higher than the above-mentioned value (e.g., 800m), there will be a certain “safety margin”, given by 0.09-(V2·g-1·R-1-0.07). For example, if R=800m, this implies a safety margin of about 0.06.
Finally, always with reference to the steering stability, but in dry conditions, for the same radius (800m), at 130km/h, in ideal conditions of friction, the radial friction would be about 0.13, and the safety margin would be 0.13-(V2·g-1·R-1-0.07)=0.04.
For the as-built pavement, in dry conditions, for the same radius, at 100km/h, the radial friction will be still 0.13, and the safety margin will be 0.13-(V2·g-1·R-1-0.07)=0.10>0.06>0.04.
Based on the above, merging the results obtained applying the criteria of the stopping distance and of the steering stability, under the hypothesis of having just one posted limits (wet or dry conditions), the new speed limit is 100km/h (equation 22).
CONCLUSION AND RECOMMENDATIONS
The following conclusion and recommendations are drawn:
- Assessing lower speed limits is crucial to save lives and to maintain a satisfactory safety level despite unsatisfactory friction coefficients;
- Braking distance and stability in curve (in wet and dry conditions) are the two main principles that can be used to assess speed limits based on rational criteria;
- When dealing with interface friction, transitioning from wet-60km/h-transverse conditions to real phenomena is a difficult task, but modelling can be carried out based on real data and without neglecting judicial background;
- Although further developments and refinements are in progress, the algorithms and the criteria set up above: i) are well grounded in logic because they build on friction theory; ii) comply and allow complying with national standards (nation-based calibration of calibration factors); iii) permit deriving the speed limits based on easy-to-use spreadsheets;
- It is recommended to apply the methodology above, (i) starting from the analysis of the friction data (position and dispersion indicators) and how they relate to stopping distance and steering stability (based on design standards); (ii) having a clear understanding of the overall trend of as-design and as-built friction values as depicted in Fig. (3); (iii) considering both dry and wet conditions; (iv) double checking if the equations, for the case under analysis, comply with the as design conditions (zero of the problem). To this end, a simple excel spreadsheet can be used for immediate control.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Decleared none.


