All published articles of this journal are available on ScienceDirect.
Modeling Heterogeneous Fleet Vehicle Allocation Problem with Emissions Considerations
Abstract
Aims:
This study proposes a bi-objective linear integer programming model for heterogeneous fleet VAP with emissions considerations. Profit maximization and emissions minimization objectives are employed to handle economic and environmental sustainability purposes.
Background:
Our literature survey shows that there is no model for the heterogeneous fleet VAP with emissions considerations that simultaneously consider vehicle heterogeneity, penalty costs for unmet demands, and emissions from transportation operations.
Objective:
The model is employed to also make several scenario analyses on sustainable freight logistics management to understand the trade-offs among economic and environmental objectives. In freight transportation problems, decision-makers need to be able to maintain profitability and to reduce emissions.
Methods:
In this study, a bi-objective linear integer programming model is proposed for a heterogeneous fleet Vehicle Allocation Problem (VAP) with emissions considerations encountered in the field of sustainable freight transportation.
Results:
In the numerical analyses, various practical assumptions that can be confronted by decision-makers in real life are discussed. In each analysis, total profit and emissions amounts are revealed along with several other KPIs. The results of the analyses provided in this study could also be useful in terms of understanding the relations among pillars of sustainability in VAPs.
Conclusion:
It is thought that the proposed model has the potential to aid decision-making processes in sustainable logistics management.
In the base case analyses, the total profit obtained under profit maximization is about nine times higher than that obtained under emissions minimization. When the aim is to minimize emissions, the total emissions are found to be nearly one-tenth of that of profit maximization. Supported by also additional scenario analyses, it can be concluded that it might not economically viable to be environmentally-friendly for companies. Therefore, companies have to be encouraged or forced to take environmentally and socially responsible actions through legislation. The analyses demonstrated that various legislative policies on emissions may affect the transportation plans differently in such vehicle allocation systems.
1. INTRODUCTION
Sustainability is a vital necessity for today’s companies while planning their logistics activities, as a result of increasing competition and the growing environmental problems, such as greenhouse gas emissions, depletion of natural resources, global warming climate change [1]. Sustainability was handled at the United Nations World Summit in 2005 in terms of three pillars, the economic, environmental, and social dimensions. It was stated that these dimensions can not be evaluated indepen- dently. According to Hart (1999), the environment includes society and society covers the economy, and these three dimensions affect each other. Accordingly, the suggestion is to initially ensure environmental sustainability, as it is not possible to achieve economic and social sustainability without achieving environmental sustainability [2].
With the growing concerns on sustainability, a new concept of “Sustainable Logistics Management” has emerged [3]. The importance of environmental and social impacts related to freight transportation has started to be recognized by governments, markets, and private institutions due to incre- asing externalities about the environment. To ensure sustain- able logistics, the efficiency of freight transport should be increased, and the environmental externalities associated with logistics should be mitigated [4, 5]. Therefore, sustainable logistics management focuses on environmental goals such as greenhouse gas reduction, ensuring energy efficiency, or waste reduction, in addition to various economic goals such as profit maximization or cost minimization [6, 7].
Road freight transport is of great value in terms of economic development and supply chain management; how- ever, it also has many harmful effects on both human health and the environment. Transportation activities account for 27% of total global CO2 emissions, and among transportation activities, the largest CO2 producer is highway freight transport with 78.8% [8]. Traditional attempts on freight transport often focus on economic dimensions and ignore negative enviro- nmental externalities. However, alleviating negative exter- nalities in freight transport in recent years has become the forefront with the growing importance of environmental targets [9].
One of the main decisions to be made within the scope of freight transport is vehicle allocation decisions. According to the definition made by Ghiani, Laporte, and Musmanno (2004), Vehicle Allocation Problems (VAPs) deal with the allocation of vehicles in the logistics system faced by carriers that generate revenue by transporting goods over long distances [10].
In VAPs, a number of vehicles are demanded to fulfill direct shipments between node pairs in a finite planning horizon. After the delivery and unloading of the cargo, the vehicles either take a new load from their current node or are repositioned to another node by making an empty trip to meet other future direct shipments. It is also possible for vehicles to stay idle in current positions before making either of the aforementioned choices. In VAPs, the aim might be to maximize profit, minimize cost/emissions, or achieve these goals together. While achieving these goals, the movements of both loaded and unloaded vehicles have to be decided.
In this study, a bi-objective linear integer programming model is proposed for a heterogeneous fleet Vehicle Allocation Problem (VAP) with emissions considerations encountered in the field of sustainable freight transportation. The proposed model allows either to maximize profit or minimize emissions for the addressed problem. The model respects different vehicle types (in terms of capacity and fuel consumption) in the fleet mix and includes a penalty for demand rejection (unmet demand). The consideration of emissions and profit along with heterogeneous fleet and demand rejection possibility are confronted in real-life problems, and therefore, are important for logistics decision-makers. To the best of our knowledge, there is no model in the related literature for a VAP that takes these dimensions simultaneously. The potential benefits of the proposed model as a result of its applicability and use are demonstrated by extensive numerical analyses.
The rest of the paper is structured as follows. In the second section, the relevant literature is presented briefly to demons- trate the contribution of our study. In the third section, a formal problem definition is provided. In the fourth section, the proposed mathematical model for the problem is explained. In the fifth section, numerical analyses on a logistics chain operating in Turkey are presented. The last section provides conclusions and suggestions for future studies.
2. METHODS
In this study, a mathematical model is proposed for VAP. Therefore, quantitative studies involving mathematical models are examined here in detail. For the literature review, we have searched for the articles indexed by the Web of Science (WOS) Core Collection database with the keyword, “vehicle allocation” in the “topic” field. Among the results, the studies which are irrelevant to our study or do not involve mathematical models are eliminated. Table 1 presents the summary of the remaining studies in terms of problem type, modeling type, objective, vehicle type, the penalty for unmet demand, and sustainability concerns.
| # | Article | Problem Type |
Model Type |
Objective | Vehicle Type | Penalty for Unmet Demand | Sustainability |
|---|---|---|---|---|---|---|---|
| 1 | Powell,1986 [11] | VAP | IP | Profit max | − | − | − |
| 2 | Hughes and Powell,1988 [12] | VAP | LP | Profit max | − | − | − |
| 3 | Frantzeskakis and Powell, 1990 [13] | VAP | SP | Profit max | − | − | − |
| 4 | Beaujon and Turnquist, 1991 [14] | VAP | MIP | Revenue max | − | √ | − |
| 5 | Birge and Ho, 1993 [15] | NP | SP | Cost min | − | − | − |
| 6 | Powell and Frantzeskakis, 1994 [16] | NP | SP | Cost min | − | − | − |
| 7 | Yan et al., 1995 [17] | NP | LP | Min platform number | − | − | − |
| 8 | Powell et al., 2000 [18] | VARP | IP | Profit max | − | − | − |
| 9 | Bojović, 2002 [19] | VRP | LP | Revenue max | − | − | − |
| 10 | Hall and Zhong, 2002 [20] | ICP | Analytic | - | − | − | − |
| 11 | List et al., 2003 [21] | FAP | SP-RO | Cost min | √ | √ | − |
| 12 | Sung and Song, 2003 [22] | NP | LP | Cost min | √ | − | − |
| 13 | List et al., 2006 [23] | FAP | SP | Cost min | − | √ | − |
| 14 | Simonetto and Borenstein, 2007 [24] | VARP | MIP | Cost min | √ | − | − |
| 15 | Lee et al., 2008 [25] | VRP | MIP | Revenue max | √ | − | − |
| 16 | Fan et al., 2008 [26] | VAP | SP | Profit max | − | − | − |
| 17 | Wu et al., 2009 [27] | VAP | IP | Total evacuation time min | √ | − | − |
| 18 | Sayarshad and Ghoseiri, 2009 [28] | VAP | IP | Revenue max | − | √ | − |
| 19 | Sayarshad et al., 2010 [29] | VAP | MO-MIP | Cost min, profit max, and fleet size min | √ | √ | − |
| 20 | Wu et al., 2010 [30] | VARP | MO-MIP | Emissions and cost min | √ | − | √ |
| 21 | Javadian et al., 2011 [31] | TP | IP | Cost min | √ | √ | − |
| 22 | Tan et al., 2011 [32] | VAP | FLP | Total evacuation time min | √ | − | √ |
| 23 | Ibri et al., 2012 [33] | VAP | IP | Traveling time min | − | √ | − |
| 24 | Milenković and Bojović, 2013 [34] | VAP | FLP | Cost min | − | √ | − |
| 25 | Shi et al, 2014 [35] | FAP | SP | Cost min | − | − | − |
| 26 | Zolfagharinia and Haughton, 2014 [36] | PDP | MIP | Profit max | − | √ | − |
| 27 | Upadhyay and Bolia, 2014 [37] | SPP | IP | Profit max and cost min | − | √ | − |
| 28 | Upadhyay and Bolia, 2014 [38] | VAP | MILP | Profit max | − | √ | − |
| 29 | Hanczar and Peternek, 2015 [39] | VAP | MIP | Empty wagon min | − | − | − |
| 30 | Andrade and Cunha, 2015 [40] | VAP | MIP | Total time min | √ | − | − |
| 31 | Atasoy et al., 2015 [41] | VAP | LP | Profit max | − | − | − |
| 32 | Milenković et al., 2015 [42] | VAP | NLP | Cost min | √ | − | − |
| 33 | Tari and Hashemi, 2016 [43] | TP | MIP | Cost min | √ | − | − |
| 34 | Zolfagharinia and Haughton,2016 [44] | PDP | MIP | Profit max | − | − | − |
| 35 | Liu et al., 2016 [45] | VAP | MIP | Demand max | √ | − | − |
| 36 | Sánchez-Martínez et al., 2016 [46] | VAP | IP | Service quality max | − | − | − |
| 37 | Vasco and Morabito, 2016 [47] | VAP | IP | Profit max | √ | − | − |
| 38 | Mesa-Arango and Ukkusuri, 2017 [48] | VAP | SP | Profit max | − | − | − |
| 39 | Kaewpuang et al., 2017 [49] | VAP | SP | Cost min | − | − | − |
| 40 | Buuren et al., 2018 [50] | VAP | MIP | Cost min | − | − | − |
| 41 | Khayati and Kang, 2019 [51] | HAPP | MILP | Travel differences min | √ | − | √ |
| 42 | Sullivan et al., 2019 [52] | VAP | MIP | Travel time min | √ | − | − |
| 43 | Pitakaso et al., 2019 [53] | VARP | MIP | Cost min | − | − | − |
| 44 | Rui et al., 2019 [54] | VAP | IP | Total utility max | − | − | − |
| 45 | Gkiotsalitis et al., 2019 [55] | VAP | NLP | Cost min | − | − | − |
| 46 | Li et al., 2019 [56] | VAP | MIP | Profit max | √ | √ | − |
| Our study | VAP | BO-IP | Profit max and emissions min | √ | √ | √ |
In addition to the studies that directly address a basic VAP, several others listed in Table 1 address variants of VAPs, such as transportation problems, fleet assignment problems, vehicle allocation and routing problems. Several objective functions, such as profit maximization, cost minimization, or time minimization are used in these attempts. Some studies also involve multi-objective models [29, 30]. A number of studies take vehicle type differences into account. In the studies of Sayarshad et al. (2010), Javadian et al. (2011), and Vasco and Morabito (2016), vehicle types are divided into two, as vehicles owned by enterprises and vehicles rented from third parties [29, 31, 47]. Differences in vehicle features are also considered by List et al. (2003) and Lee et al. (2008) [21, 25]. Studies such as Beaujon and Turnquist (1991), and Zolfagharinia and Haughton (2014) incorporate penalty costs due to unmet demands into their models [14, 36].
Among the reviewed studies, three of them consider emissions and address a sustainability issue. Wu et al. (2010) address the optimization of evacuations from urban areas [30]. The model proposed in the study respects vehicle allocation in case of evacuation and optimizing the routes of the vehicles. The model involves three different objective functions as minimizing mobile emissions, minimizing the total evacuation time, and minimizing costs. The model does not respect vehicle heterogeneity and penalty costs for unmet demand. Tan et al. (2011) define the objective function in their mathematical model as ensuring minimization of evacuation time [32]. Besides, the total emissions amount in the model is considered as a constraint, and it is aimed to keep the total emissions amount at a certain level while minimizing the discharge time. Different vehicle types are considered in the model; however, penalty costs for unmet demand are not taken into account. Khayati and Kang (2019) make a comparison of electric vehicles with internal combustion engine vehicles [51]. It was stated that the increase in the use of electric vehicles has positive effects on the environment in terms of emitted emissions. The model does not incorporate emissions estimations while making decisions. The use of electric vehicles instead of conventional ones could provide huge contributions in terms of sustainable logistics. Yet, their impact on the market has not been as extensive as expected for several reasons, such as limited range, low load-carrying capacity, insufficient charging stations infrastructure (see, e.g., Cavallaro et al., 2018 [66], Fioreze et al., 2019 [67], Saleh & Hatzopoulou, 2020 [68], Soysal et al., 2020 [69], Asadi et al., 2021 [70]).
Our literature survey shows that there is no model for the heterogeneous fleet VAP with emissions considerations that simultaneously consider vehicle heterogeneity, penalty costs for unmet demands, and emissions from transportation opera- tions. The model is employed to also make several scenario analyses on sustainable freight logistics management to understand the trade-offs among economic and environmental objectives. In freight transportation problems, decision-makers need to be able to maintain profitability and reduce emissions. For this reason, it is thought that the proposed model has the potential to aid decision-making processes in sustainable logistics management.
3. PROBLEM DESCRIPTION
The addressed VAP has a given number of nodes (e.g., cities), N = {1,2, …,|N|}. The nodes are considered as cities among which transportation operations are performed. Meeting available requests generate revenue. The fleet that serves transportation requests comprises heterogeneous vehicles, each of which belongs to a different vehicle type (A = {1,2, …,|A|}). Each vehicle type is characterized by capacity and fuel consumption rate values. The type of vehicle that can be used to meet demand is dependent on the corresponding customer request. At least one vehicle type is suitable to meet each request of customers. The optimal vehicle allocation decisions are made for a finite planning horizon (T={1,2, …,|T|}).
Demands (dijt) occur as vehicle requests between city pairs during the planning horizon. For example, if δ vehicles are required for transporting related goods from node i to node j in period t, then dijt = δ. Meeting a fraction of demand is allowed, which means that if there are δ requests from node i to j in period t, it is possible to meet any (integer) amount smaller than or equal to δ.
Transportation costs comprise two components as fuel consumption and fixed costs for dispatching vehicles. Estimating total fuel consumption as a result of transport activities also allows us to estimate transportation emissions. The penalty costs in the problem arise in two ways. The first is the penalty of unmet demand (sijt). The second is the penalty that represents the opportunity cost of moving empty vehicles (cij). These penalty costs do not vary depending on the vehicle type. Travel time varies depending on the distance between destination and arrival nodes of the transportation activity.
There is a demand fulfillment rate for each node. The value of this rate indicates the minimum ratio of the total demand over the planning horizon that must be met for each node in the system. The purpose of using this target is to prevent large differences between the demand fulfillment ratios among the nodes. Preventing such differences ensures a fair delivery service to each node, which will have a positive contribution in terms of customer satisfaction and loyalty.
The problem aims to determine empty or loaded vehicle movements in the logistics system during the planning horizon, which either maximizes profit or minimizes emissions.
3.1. A Bi-objective Integer Linear Programming Model for the Problem
Table 2 presents the notation (sets, parameters, variables) used in the bi-objective integer linear programming model proposed for the VAP that considers transportation emissions.
| Symbol | Description | Unit |
|---|---|---|
| Sets | - | - |
| N | Set of nodes where loads are taken from and delivered to {1,2, …,|N|} | - |
| A | Set of vehicle types {1,2, …,|A|} | - |
| T | Set of time periods {1,2, …,|T|} | - |
| Parameters | - | - |
| rij | Revenue obtained from each vehicle transporting goods from node i to j | TL/unit |
| ffa | The fuel consumption rate of a loaded vehicle with type a per km | liter/km |
| faa | The fuel consumption rate of an empty vehicle with type a per km | liter/km |
| fc | Fuel cost per liter | TL/liter |
| disij | Distance between nodes i and j | km |
| fixija | Fixed dispatching cost of the vehicle with type a used for transportation from node i to j | TL/unit |
| cij | Penalty cost of empty travels from node i to j | TL/unit |
| sijt | Penalty cost for unmet demand between nodes i and j in period t | TL/unit |
| efa | Emissions rate of a loaded vehicle with type a per km | gr/km |
| eaa | Emissions rate of an empty vehicle with type a per km | gr/km |
| ρki | Lead time between nodes i and j | day |
| mita | Number of newly available vehicles with type a in node i at period t | Unit |
| dijt | Number of demand from node i to j in period t | Unit |
| lijta | 1 if vehicle type a is suitable to satisfy demand from node i to j at period, 0 otherwise | (0,1) |
| α | The demand fulfillment rate required for a fair distribution at each node | [0,1] |
| M | A sufficiently large number | - |
| Decision variables | - | - |
| Xijta | Number of loaded trips with vehicle type a from node i to j at period t | Unit |
| Yijta | Number of empty trips with vehicle type a from node i to j at period t, where Yii0a = 0,i ϵ N,a ϵ A | Unit |
The proposed bi-objective integer linear programming model is developed based on the integer linear programming model proposed by Ghiani, Laporte, and Musmanno (2004) [10]. As distinct from their model, the proposed model here involves two objective functions. While the objective function in the study of Ghiani et al. (2004) was only profit maximization, the objective functions in this study are to maximize the profit and to minimize the emissions [10]. Besides, our model respects penalty costs for unmet demand and different vehicle types while satisfying requests. Ghiani et al. (2004) assume that all existing vehicles are suitable for transportation; however, in the proposed model here, the suitability of vehicles for transportation is taken into consideration [10].
The proposed bi-objective linear integer programming model that is developed to address a heterogeneous fleet VAP by considering the economic and environmental factors is presented below. The relevant model has two objective functions (1), (2), and six constraint sets (3, …, 8).
Maximize (Profit)
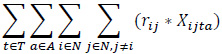 |
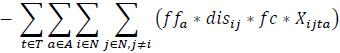 |
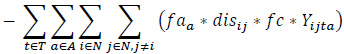 |
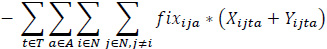 |
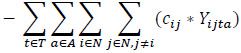 |
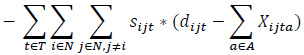 |
(1) |
Minimize (Emissions)
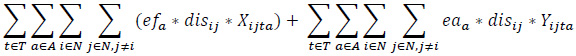 |
(2) |
Subject to
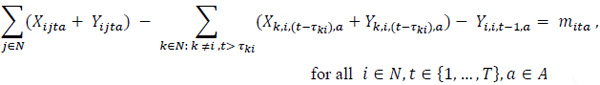 |
(3) |
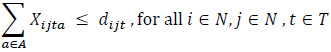 |
(4) |
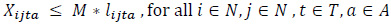 |
(5) |
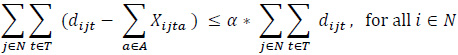 |
(6) |
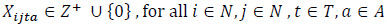 |
(7) |
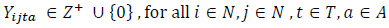 |
(8) |
The objective function (1) consists of revenue, fuel cost for loaded vehicles, fuel cost for empty vehicles, fixed costs, a penalty of moving empty vehicles, a penalty of unmet demand. The objective function (2) expresses the total emissions of the vehicles employed.
The constraint set (3) balances vehicle flows by taking into account full and empty vehicle movements. The constraint set (4) states that the number of loaded vehicles moving between node pairs has to be smaller than or equal to the corresponding demand in the same period. The constraint set (5) indicates that the types of loaded vehicles should be in line with customer requests regarding that demand. The constraint set (6) ensures that the unmet demand is kept at a certain level for each node and that the incoming requests are met fairly. The demand fulfillment rate, α, is a user-defined parameter that takes a value between 0 and 1. The constraint sets (7) and (8) define the restrictions on the decision variables.
4. RESULTS AND DISCUSSION
This section shows an implementation of the proposed model on a data set obtained from a logistics network operating in Turkey. The “e-constraint approach” proposed by Andersson (2000) is employed while solving the bi-objective model [57]. The e-constraint approach is based on restructuring the model by keeping one of the objectives in the objective function and using the other one as an additional constraint. The additional constraint is bounded by an epsilon value (ϵ). The value of ϵ is specified explicitly for each set of analyses.
The linear integer programming model for the profit maximization case is given below:
 |
The linear integer programming model for the emissions minimization case is given below:
 |
In what follows, we first describe the data used, and then show the results.
4.1. Data Description
The addressed logistics problem comprises 30 cities (N = {1, 2, …, 30}). The network is complete, therefore, intercity transportation among all nodes can be done. Fig. (1) shows the representation of the logistics network. The planning horizon is 15 days (T = {1, 2, …, 15}).
Lead times (τki) vary depending on the length of the distance between nodes. Lead time is assumed to be one day when the distance between nodes is less than or equal to 499 kilometers. For lengths between 500-999 kilometers and equal to or longer than 1000 kilometers, lead times are two and three days, respectively.
Data for demand (dijt), vehicle suitability based on requests (lijta), and the number of newly available vehicles at each node (mita) are generated arbitrarily. It is assumed that there are 6546 requests between nodes throughout the entire planning horizon, no penalties are applied for unmet demands and empty travels, and there exist initially 225 vehicles at different nodes in the network. Apart from these vehicles, there is no new vehicle entry throughout the planning horizon.
Demands between city pairs are satisfied by heterogeneous vehicles. Each vehicle belongs to one of seven types (A = {1, 2, …, 7}). There are two main vehicle types in the problem as standard and refrigerated vehicles [58]. Each of these main types has sub-types. It is assumed that there are 3 sub-types of standard vehicles with different carrying capacities, 18, 26, and 32 tonnes. There are 4 sub-types of refrigerated vehicles, which are formed by a combination of two features, age (new or old) and capacity (12 or 15 tonnes).
Fuel consumption rates are generated arbitrarily using a similar approach followed by Hoen et al. (2014) [59]. The vehicle type with the smallest carrying capacity (12 tonnes) is assumed to have the least fuel consumption rate. The other rates are determined accordingly, assuming that the fuel consumption rates are dependent on vehicle type, carrying capacity, and being empty or fully-loaded. Table 3 provides the fuel consumption rates (liter/km) of vehicle types used in the logistics network. Fuel consumption is converted into emissions rates through a fuel conversion factor, which is assumed as 2.63 gr/liter [60, 61].
The fuel price per liter is taken as 6.08 TL/liter [62]. Several approaches are used to calculate logistics costs in long haul freight transportation. We assume that fixed dispatching cost is dependent on traveled time or distance, as the longer the distance is, the longer the travel time and the corresponding preparation and opportunity costs will be. Here, the fixed cost is taken as equal to the fuel consumption cost at each travel. The revenue generated by the demands met is calculated by taking vehicle types into account. It is assumed that the obtained revenue is 1.5 times the sum of fuel and fixed costs of a hypothetical fully-loaded vehicle with a fuel consumption rate that is the average of the seven-vehicle types. The demand fulfillment rate (α) required for fair distribution at each node is assumed to be 10%. The summary of all the data is shown in the Appendix 1.
For the numerical analysis, IBM OPL ILOG CPLEX 12.9 software is utilized to develop and solve the proposed mathematical model. The relative MIP gap tolerance is set to 0.1%. The solutions are obtained within approximately five minutes on average using an HP Pavilion i5 computer with 8 GB memory with 1.8 GHz processor.
4.2. Base Case Solution
Both profit maximization and emissions minimization objectives are analyzed for the base case. For profit maximization, the epsilon value (ϵ1) required for the emissions constraint is set to 1,000,000 grams. For emissions minimization, ϵ2 required for the total profit constraint is set to 100,000 TL. Table 4 provides the results of the conducted analyses according to several Key Performance Indicators (KPIs).
According to the solution obtained under profit maximization, the total profit is 2,503,380 TL and the total emissions are 999,973 grams. In the case of emissions minimization, the solution indicates that the total profit is 284,425 TL, and the total emissions value is 103,257 grams.
| Vehicle Type | Rate (Empty, liter/km) | Rate (Fully-loaded, liter/km) |
|---|---|---|
| 1 (Standard - 18 tonne) | 0.26 | 0.312 |
| 2 (Standard - 26 tonne) | 0.286 | 0.3432 |
| 3 (Standard - 32 tonne) | 0.3146 | 0.37752 |
| 4 (Refrigerated - 12 tonne/new) | 0.2 | 0.24 |
| 5 (Refrigerated - 15 tonne/new) | 0.22 | 0.264 |
| 6 (Refrigerated - 12 tonne/old) | 0.24 | 0.288 |
| 7 (Refrigerated -15 tonne/old) | 0.264 | 0.3168 |
| Key Performance Indicators | Profit maximization | Emissions minimization |
|---|---|---|
| Total revenue (TL) | 7,126,828 | 761,843 |
| Total fuel cost of loaded vehicles (TL) | 2,311,724 | 238,664 |
| Total fuel cost of empty vehicles (TL) | 0 | 45 |
| Total fixed cost of operating vehicles (TL) | 2,311,724 | 238,709 |
| Total penalty cost for unmet demand (TL) | 0 | 0 |
| Total penalty cost for empty travels (TL) | 0 | 0 |
| Total cost (TL) | 4,623,448 | 477,418 |
| Total profit (TL) | 2,503,380 | 284,425 |
| Total emissions from loaded vehicles (gr) | 999,973 | 103,238 |
| Total emissions from empty vehicles (gr) | 0 | 19 |
| Total emissions (gr) | 999,973 | 103,257 |
| Total number of loaded trips (in unit) | 1,600 | 669 |
| Total number of empty trips (in unit) | 0 | 1 |
| Total number of stationary (non-moving) vehicles (in unit) | 531 | 2,702 |
| Total distance travelled (km) | 1,308,880 | 147,968 |
| Demand fulfillment rate | ≥10% | ≥10% |
The results show that the total profit obtained under profit maximization is about nine times higher than that obtained under emissions minimization. When the aim is to minimize emissions, the total emissions are found to be nearly one-tenth of that of profit maximization.
When the objective is to minimize the emissions, the model is constrained by the demand fulfillment rate (10%) and the minimum total profit constraint (100,000 TL). Accordingly, a relatively fewer number of loaded trips for emissions minimization occurred compared to profit maximization. Out of the total of 6,546 requests, 1,600 units are satisfied under profit maximization and 669 units are satisfied under emissions minimization. Note that the total distance traveled is also parallel with the number of requests met.
According to the fuel consumption and emissions rates, vehicles types can be listed in ascending order as follows: 4 < 5 < 6 < 1 < 7 < 2 < 3. As can be observed from Table 5, cost and emissions performances of vehicle types play a significant role in being selected for meeting demand. This shows the potential benefit of taking vehicle heterogeneity into account.
4.3. Scenario Analyses on Sustainable Freight Transportation
This section analyzes and compares the solutions obtained for several other scenarios in addition to the base case. In these scenarios that are likely to occur in real life, the aim is to observe the effects of parameter changes on several KPIs.
4.3.1. Positive Penalty Costs
Note that for the base case, the penalty cost of unmet demands (sijt) is assumed to be zero. Random nonnegative numbers are assigned to these parameters in this analysis. The assigned numbers are provided in the supplementary data file.
In profit maximization, the profit decreased from 2,503,380 TL to 2,452,109 TL due to the penalty cost component in the objective function, without a significant change in the total emissions (Table 6). The number of requests met increased from 1,600 to 1,679 units to lessen the penalty costs of demand rejection. Despite the increase in the number of demands met, total revenue decreased from 7,126,828 TL to 7.112,039 TL. In addition to this, the added penalty cost led to a decrease in total profit. In emissions minimization, the total profit decreased from 284,425 TL to 184,393 TL without a significant change in the total emissions (Table 6). The number of demands met did not change.
This analysis shows that additional economic concerns might alter the transportation plans, and therefore, corres- ponding decision support models should account for such dimensions.
4.3.2. Emissions Tax
Transportation emissions tax is a strategy implemented by governments to maintain sustainable development [63]. While analyzing the emissions tax scenario, 1 TL emissions tax was added per each gram of emissions.
For profit maximization and emissions minimization, the amounts of total emissions generated were not affected significantly, as a serious change was not observed in the total number of loaded trips. However, additional emissions tax causes total costs to increase, and this results in a total profit decrease for both cases. Total profit decreased from 2,503,380 TL to 1,503,849 TL for profit maximization, and from 284,425 TL to 181,071 TL for emissions minimization (Table 6).
The results show that increased cost of transportation due to additional emissions tax does not reduce environmental externalities significantly but reduces total profit to be observed. A basic emissions tax policy might not always be sufficient to improve the environmental performance of supply chains.
| Vehicle Type | Fuel Consumption Rate (Fully-Loaded, Liter/km) | Profit Maximization | Emissions Minimization |
|---|---|---|---|
| 4 (Refrigerated /12 tonne/new) | 0.24 | 209 | 267 |
| 5 (Refrigerated /15 tonne/new) | 0.264 | 267 | 195 |
| 6 (Refrigerated /12 tonne/old) | 0.288 | 304 | 101 |
| 1 (Standard - 18 tonne) | 0.312 | 328 | 48 |
| 7 (Refrigerated /15 tonne/old) | 0.3168 | 252 | 34 |
| 2 (Standard-26 tonne) | 0.3432 | 192 | 14 |
| 3 (Standard-32 tonne) | 0.37752 | 48 | 10 |
| - | - | - | Scenarios | |
|---|---|---|---|---|
| - | Indicators | Base Case |
Penalty Costs |
Emissions Tax |
| Profit maximization | Total Profit (TL) | 2,503,380 | 2,452,109 | 1,503,849 |
| Total Emissions (gr) | 999,973 | 999,994 | 999,785 | |
| Total Cost (TL) | 4,623,448 | 4,659,930 | 5,622,363 | |
| Emissions minimization | Total Profit (TL) | 284,425 | 184,393 | 181,071 |
| Total Emissions (gr) | 103,257 | 103,235 | 103,235 | |
| Total Cost (TL) | 477,418 | 577,231 | 580,553 | |
4.3.3. Homogeneous Vehicles
While planning delivery operations, heterogeneous vehicles are considered in the base case. In case the vehicle types are not taken into account, the relevant analysis has been made using the average of the loaded/unloaded fuel consumption rates of the 7 vehicle types specified in Table 3. The fuel consumption rates of the vehicle in the loaded and unloaded states are taken as 0,255 and 0,306 liter/km, respectively. This means that fuel consumption was calculated roughly without respecting vehicle heterogeneity. Table 7 provides the results of homogeneous vehicle analyses with rough and real fuel calculations.
According to the results, the rough fuel calculation leads to inexact total profit and emissions. For profit maximization, the total profit was roughly determined as 2,247,981 TL, however, the corresponding real profit was calculated as 2,226,237 TL when the vehicle heterogeneity was taken into account. The real fuel calculation shows that for both profit maximization and emissions minimization, the total profits have decreased and total emissions have increased compared to the base case solution. The number of vehicles used from each type presented in Table 8 also shows that vehicles with relatively higher fuel consumption rates are more frequently used compared to that of the base case (Table 5). Therefore, it can be concluded that not respecting heterogeneous vehicles results in suboptimal delivery plans in terms of both profit and emissions. The results on the benefits of respecting vehicle heterogeneity are in line with the findings of the studies existing in the related literature, such as the studies conducted by Bektaş and Laporte (2011) and Demir et al. (2012) [64-70].
| Key Performance Indicators | Profit Maximization | Emissions Minimization | Profit Maximization | Emissions Minimization |
|---|---|---|---|---|
| Rough fuel calculation | Real fuel calculation | |||
| Total revenue (TL) | 6,872,479 | 742,291 | 6,872,479 | 742,291 |
| Total fuel cost of loaded vehicles (TL) | 2,312,249 | 268,445 | 2,323,121 | 272,413 |
| Total fuel cost of empty vehicles (TL) | 0 | 0 | 0 | 0 |
| Total fixed cost of operating vehicles (TL) | 2,312,249 | 268,445 | 2,323,121 | 272,413 |
| Total penalty cost for unmet demand (TL) | 0 | 0 | 0 | 0 |
| Total penalty cost for empty travels (TL) | 0 | 0 | 0 | 0 |
| Total cost (TL) | 4,624,498 | 536,890 | 4,646,242 | 544,826 |
| Total profit (TL) | 2,247,981 | 205,401 | 2,226,237 | 197,465 |
| Total emissions from loaded vehicles (gr) | 999,976 | 116,094 | 1,004,902 | 117,836 |
| Total emissions from empty vehicles (gr) | 0 | 0 | 0 | 0 |
| Total emissions (gr) | 999,976 | 116,094 | 1,004,902 | 117,836 |
| Total number of loaded trips (in unit) | 1,786 | 669 | 1,786 | 669 |
| Total number of empty trips (in unit) | 0 | 0 | 0 | 0 |
| Total number of stationary (non-moving) vehicles (in unit) | 362 | 2,705 | 362 | 2705 |
| Total distance travelled (km) | 1,242,824 | 144,288 | 1,242,824 | 144,288 |
| Demand fulfillment rate | ≥10% | ≥10% | ≥10% | ≥10% |
| Vehicle Type | Fuel Consumption Rate (Fully-loaded, liter/km) | Profit Maximization | Emissions Minimization |
|---|---|---|---|
| 4 (Refrigerated /12 tonne/new) | 0.24 | 202 | 82 |
| 5 (Refrigerated /15 tonne/new) | 0.264 | 271 | 88 |
| 6 (Refrigerated /12 tonne/old) | 0.288 | 277 | 90 |
| 1 (Standard - 18 tonne) | 0.312 | 303 | 135 |
| 7 (Refrigerated /15 tonne/old) | 0.3168 | 243 | 59 |
| 2 (Standard-26 tonne) | 0.3432 | 191 | 101 |
| 3 (Standard-32 tonne) | 0.37752 | 299 | 114 |
| - | Profit Maximization | Emissions Minimization | ||
|---|---|---|---|---|
| Demand Fulfillment Rates | Total Profit (TL) | Total Emissions (gr) | Total Profit (TL) | Total Emissions (gr) |
| 20% | 2,438,226 | 999,982 | 711,334 | 291,130 |
| 10% | 2,503,380 | 999,973 | 284,425 | 103,257 |
| 0% | 2,512,686 | 999,972 | 100,035 | 23,772 |
4.3.4. Changes in Demand Fulfillment Rate
The demand fulfillment rate is defined as the value that indicates how much of the demands that occur during the whole planning horizon for each of the nodes have to be satisfied. The value of this parameter (α) is assumed to be 0.9 in the base case. Table 9 presents the obtained results for different demand fulfillment rates.
For profit maximization, the increase in demand fulfillment rate results in a decrease in total profit. The reason is the fact that the increase in demand fulfillment rate results in the necessity to meet transportation requests that generate lower revenues. Since there is no such requirement at 0% demand meeting level, total profit can be obtained even though less demand is met. Considering the total number of movements of loaded vehicles, it is observed that there are 1,772 loaded trips when the level of meeting the demand is 20%, 1,600 loaded trips when 10%, and 1532 loaded trips when 0%.
For emissions minimization, the increase in demand fulfillment rate increases total profit and total emissions. Considering the total number of movements of loaded vehicles, it is 1,322 when the level of meeting the demand is 20%, 669 when 10%, and 68 when 0%. When the demand fulfillment rate is taken as 0%, the model does not have to achieve a fair distribution among nodes while satisfying the minimum profit constraint (ϵ2).
Ensuring fair distribution at each node in the logistics network might be considered as a social sustainability target for transportation companies. The provided results here show the potential trade-offs between this target and the other two pillars of sustainability. That is, tightening demand fulfillment rates may cause worse economic and environmental externalities.
4.3.5. The Trade-off between Profit and Emissions
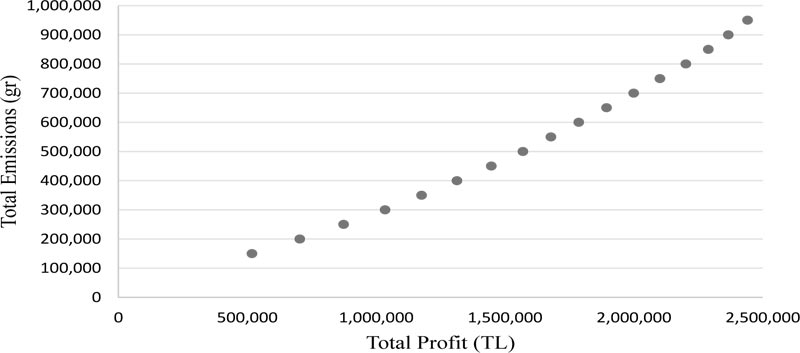
Here we examine the total profits encountered at different emissions levels. While making total emissions pareto analysis, profit maximization is used as an objective function and total emissions amount is accepted as an e-constraint.
Solutions have been reached by gradually increasing the total emissions amount (ϵ3) in grams from 150,000 up to 950,000 grams by 50,000 grams increments. The pareto graph of the profit and emissions values is shown in Fig. (2).
This analysis reveals that economic concerns might result in worse environmental performance. According to the results, in order to obtain higher profits, higher amounts of emissions have to be endured. The conclusion is that there is no economic incentive for companies to be environmentally friendly. Therefore, emissions restrictions on the logistics network to mitigate transportation emissions are required to alleviate negative externalities despite the corresponding profit decrease. It would also be useful for decision-makers to estimate the cost of being environmentally-friendly while planning freight distribution. Moreover, there are more than just economic incentives. Currently, there is already a slight increase in customers requesting transparency in environmental performance, and choosing those companies which perform better (sometimes even willing to pay extra for a more environmentally friendly service). In time, reducing the environmental footprint might become a license to operate, and companies not paying attention to their impact might lose out on business.
| Key Performance Indicators | Profit Maximization |
|---|---|
| Total revenue (TL) | 7,115,515 |
| Total fuel cost of loaded vehicles (TL) | 2,311,774 |
| Total fuel cost of empty vehicles (TL) | 0 |
| Total fixed cost of operating vehicles (TL) | 2,311,774 |
| Total penalty cost for unmet demand (TL) | 0 |
| Total penalty cost for empty travels (TL) | 0 |
| Total cost (TL) | 4,623,548 |
| Total profit (TL) | 2,491,967 |
| Total emissions from loaded vehicles (gr) | 999,994 |
| Total emissions from empty vehicles (gr) | 0 |
| Total emissions (gr) | 999,994 |
| Total number of loaded trips (in unit) | 1,609 |
| Total number of empty trips (in unit) | 0 |
| Total number of stationary (non-moving) vehicles (in unit) | 497 |
| Total distance travelled (km) | 1,304,829 |
| Demand fulfillment rate | ≥10% |
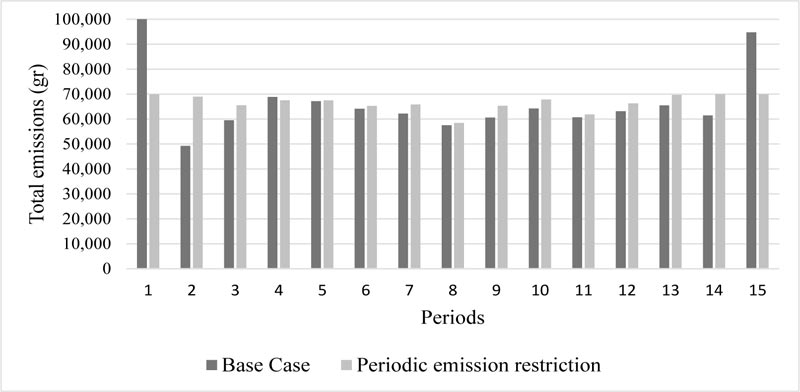
4.3.6. Periodic Emissions Analysis
In the periodic emissions analysis, the status of the emissions during each of the periods in the planning horizon will be examined for the base case. In this analysis, the case that the emissions amount should be kept under 70,000 grams for each period, in addition to the existing total emissions restriction of 1,000,000 grams, is examined. Table 10 provides an overview of the results. Fig. (3) shows the observed total emissions level of each period.
Periodic emissions restriction aims to ensure that the emissions that occur in each period are kept at a certain level. When the periodic emissions are kept at 70,000 grams for each period; it is observed that total profit decreased compared to the one obtained in the base case. According to the results presented in Fig. (3), the base case solution violates the periodic emissions restriction in periods 1 and 15. This result, in addition to the previous analysis on emissions tax, shows that various legislative policies on emissions affect the transportation plans in such vehicle allocation systems.
CONCLUSION
This study proposes a bi-objective linear integer programming model for heterogeneous fleet VAP with emissions considerations. Profit maximization and emissions minimization objectives are employed to handle economic and environmental sustainability purposes. As far as we know, this study is the first attempt to formulate and solve the addressed problem. The added value of the proposed model is presented through several numerical analyses.
In the numerical analyses, various practical assumptions that can be confronted by decision-makers in real life are discussed. In each analysis, total profit and emissions amounts are revealed along with several other KPIs. The results of the analyses provided in this study could also be useful in terms of understanding the relations among pillars of sustainability in VAPs.
In the base case analyses, the total profit obtained under profit maximization is about nine times higher than that obtained under emissions minimization. When the aim is to minimize emissions, the total emissions are found to be nearly one-tenth of that of profit maximization. Supported by also additional scenario analyses, it can be concluded that it might not be economically viable to be environmentally-friendly for companies. Therefore, companies have to be encouraged or forced to take environmentally and socially responsible actions through legislation. The analyses demonstrated that various legislative policies on emissions may affect transportation plans differently in such vehicle allocation systems.
The proposed model is generic and applicable for other VAPs confronted in long-haul freight transportation as well. In future studies, new modeling approaches can be developed by taking other relevant concerns into account, such as demand uncertainty, dynamic fleet mix, traffic density and road conditions.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
The authors confirm that the data supporting the findings of this study are available within the article.
FUNDING
None.
CONFLICT OF INTEREST
Dr. Mehmet Soysal is the Editorial Board Member of The Open Transportation Journal.
ACKNOWLEDGEMENTS
Declared none.
| Symbol | Values/Estimations | Source |
|---|---|---|
| N | {1,2, …,30} | Assumption |
| A | {1,2, …,7} | Assumption |
| T | {1,2, …,15} | Assumption |
| rij | See supplementary file | Assumption |
| ffa | Table 3 | Hoen et al. (2014) [59] https://www.truck.man.eu/tr (2019) |
| faa | Table 3 | Hoen et al. (2014) [59] https://www.truck.man.eu/tr (2019) |
| fc | 6.08 TL/l | http://www.tppd.com.tr |
| disij | Figure 1 | https://www.google.com/maps (2019) |
| fixij | See supplementary file | Assumption |
| cijija | See supplementary file | Assumption |
| sijt | See supplementary file | Assumption |
| efa | ffa * conversion | Ubeda et al. (2011) [61] |
| eaa | faa * conversion | Ubeda et al. (2011) [61] |
| τki | 0-499 km 1 day 500-999 km 2 day 1000+ km 3 day |
Assumption |
| mita | Total: 225 | Assumption |
| dijt | Total:6546 | Assumption |
| lijta | See supplementary file | Assumption |
| α | 0.9 | Assumption |
| M | A sufficiently large number | Assumption |
| conversion | 2,63 gr/l | Defra (2007) [60] |


