All published articles of this journal are available on ScienceDirect.
An Evolutionary Algorithm in Static Airport Gate Assignment Problem
Abstract
Background and Objectives:
Gate Assignment Problem is an existing issue at modern airports. Gate assignment is a complex issue in which different airports have their own demographic and geographic features although the gate and flight pattern are identical, and flights may not be assigned precisely to the gates.
Methods:
The gate assignment model would be a suitable and an appropriate tool for airport authorities to assign aircraft to gates in an effective and efficient way. The aim of the model is to assign each aircraft to an available gate to maximise both efficient operations for airports and airlines, and convenience for passengers. The model would benefit airports by improving efficiency of operations and convenience for travellers. The model illustrates how the resources are fully utilised, achieving an optimal result. This model applies the evolutionary approach to handle the gate assignment problem. The smart and generative algorithm speeds up the solving process for providing the solution within a reasonable time.
Results:
This model can reduce the business class travellers’ total walking distance by optimising the utilisation of gate resources. This has been was applied at the Taiwan Taipei Taoyuan International Airport and the results have shown an improvement in minimising the total walking distances, and the results for business class travellers are promising.
Conclusion:
A metropolitan airport usually handles more than thirty boarding gates and hundreds of flights every day. Gate assignment can help an airport to assign the gates to the flights more effectively, with the advancement of genetic algorithms. The gate assignment problem model performed a successful assignment solution within an acceptable timeframe. The proposed evolutionary algorithm gate assignment model could reduce the business class passengers’ total walking distances.
1. INTRODUCTION
The aviation industry has grown rapidly, as demonstrated by the number of passengers and cargo volume. The total cargo volume and the total number of passengers were the highest in 2014. Air cargo is a crucial enabler of the global economy. In 2014, airlines transported 51.3 million tons of goods valued at $6.8 trillion. The global average growth rate of airport passengers is 5.5%. The growth rate is even more spectacular in Asia, thanks to technological advancement, and several airports in Asia have doubled the number of passengers and the volume of air cargo in the last ten years [1-5]. Time is the second most important factor for all parties in the aviation industry, while safety and security are the most important. Each minute saved by airlines would contribute to the reduction of operations cost. Furthermore, not only have flight delays become a critical issue for airlines, but for economies too. As reported by the Bureau of Transportation Statistics of the United States, the on-time arrival rate of airlines in the US in January 2018 was 79.6%. Delays lead to financial losses for airlines; it was estimated in 2019 that practically each minute of flight delay would cost airlines in the United States US$74.24. Since the definition of a flight delay is a flight being delayed 15 minutes or more than its scheduled time, each delayed flight would entail a financial loss of at least US$1,113.60 [6, 7]. As more and more airlines enter the market, especially the Low-Cost Carriers, the demand for flights and usage of airport facilities has gradually increased [8]. Kim and Feron [9] have commented that the usage of gates and slots at airports has reached the limit in major metropolitan airports, and this might cause the problem of gate-holding. The consequence of the shortage of airport facilities would be delays, resulting in both the airport authority and the airlines suffering financial loss. The customer satisfaction level would also be lowered and customers will tend to look for alternatives. Castaing et al. [10] suggested that gate blocking may cause passenger delays and passengers will suffer missed connections. Nesset and Helgesen [11] pointed out that passengers may prefer to travel with other airlines and to use other nearby airports, or to switch to another transportation mode if gate-holding occurs frequently.
The main objective of airport operations is to provide a flexible and efficient environment to handle aircraft landing and take-off. The authority might also want to maximise the usage of the airport and reduce idle time. With the strong demand for human intelligence, a high rate of human error is expected and time is consumed in assigning aircraft to appropriate gates. This may not be suitable at a metropolitan airport. Airport Gate Assignment (AGA) is one of the tools that can work to mitigate the gate shortage problem. Solutions to the Gate Assignment Problem (GAP) should provide an expert system to optimise airport gate activities. Gate assignment programming is a crucial element for airport operation, especially in some metropolitan airports. Airport authorities have attempted to maximise gate usage and reduce idle time. Gate assignment is defined as assigning a set of flights to a set of gates while meeting certain criteria. It includes connecting passengers from the terminal and customs, immigration and quarantine (CIQ) to the gates. This is a complicated problem, as it considers a wide range of interdependent resources, including aircraft, gates, gate facilities and crews. Bolat [12] believed that the GAP also includes a group of flights with departure and arrival times specified in periods such as weekly and monthly master schedules and the consideration of some major airlines and airport authorities. GAP was first discussed in 1974, with the first GAP model being built in 1984 [13-15]. However, due to technological limitations, research conducted on GAP was limited before 2000. But in the 2000s, there was a rising trend of research on GAP and the model became more complex. Ding et al. [16] introduced a meta-heuristic approach to solving multi-objective GAP. Recently, some researchers have attempted to solve GAP by swarm intelligence. Zhao and Cheng [17] applied the ant colony optimisation method to GAP. Marinelli et al. [18] introduced the artificial bee colony optimisation into GAP as well.
This paper studies GAP at a metropolitan airport. The study aims to use a heuristic approach to solve the GAP. The focus is on using meta-heuristics to provide a solution to GAP with a feasible quick response and to minimise the walking distance of business-class travellers, as business passengers have dominated the revenue for airlines and airports. This paper also proposes a suggested gate plan for utilizing the gates at the airport. The suggested plan attempts to reduce the usage of the far gates and to reduce the overall total walking distance. Section 1 provides the background of the research on GAP, while Section 2 reviews the current literature related to GAP. Section 3 describes the problem formulation of the static GAP model with meta-heuristic algorithms. The objective function is used to minimise the total walking distance for business class travellers. Section 4 interprets the results of the GAP solved by the algorithms, and a case study is demonstrated using the setting of the Taipei Taoyuan International Airport. Section 5 offers the concluding remarks.
2. LITERATURE REVIEW
GAP is one of the most significant problems that airport authorities encounter on a daily basis. Some research has been done to solve this problem and tackle its complexity. The aims of the GAP solution are to assign each aircraft to an available gate to ensure efficient operations for airports and airlines while offering convenience to passengers. This objective requires a solution that provides the ability to update the gate assignment in real-time. It was first discussed by Steuart [19] as the Gate Position Requirement. The first known GAP was introduced by Babić et al. [20], with the objective of minimising the passengers’ walking distance. Table 1 shows some examples of different types of GAP models.
| GAP Model | Year |
Objective Function |
Features | References |
| Gate position requirement | 1974 | Maximise the efficient use of the gate positions | The first model of GAP | [19] |
| GAP | 1984 | Minimise the walking distances of passengers | First known of GAP | [20] |
| a heuristic on GAP | 1985 | Minimise the walking distances of passengers | Applied heuristic algorithm | [15] |
| Meta-heuristic on GAP | 2004 | Minimise the number of ungated flights walking distances and connection time | Applied meta-heuristic algorithm | [16] |
| Hybrid model on GAP | 2010 | Maximise the sum of all products of the flight eigenvalue and the gate eigenvalue which the flight assigned | Studied gate conflict | [21] |
| Robust GAP | 2015 | Minimise the walking distance of connecting passengers | Robust gate assignment | [22] |
| A parallel machine scheduling problem | 2017 | Minimise the total cost and tardiness | Applied heuristic and meta-heuristic approach | [23] |
2.1. Static Gate Assignment
Minimising passengers’ inconvenience has been one of the major objectives of past research. Mangoubi and Mathaisel [15] aimed at minimising total walking distance in GAP at Toronto Pearson International Airport as a real case study on minimising passenger walking distances. Similarly, Yan and Tang [24] and Lim and Wang [25] applied the same objective to the Chiang Kai-Shek Airport and Hong Kong International Airport, respectively. Ding et al. [16] attempted to minimise the number of ungated flights, whereas Dorndorf et al. [26] also tried to reduce the total walking distance or connection time. Bihr [14] and Haghani and Chen [27] tried to minimise the total passenger walking distance. Yan and Tang [24] focused on reducing the total waiting time for passengers. Genç et al. [28] effort was to maximise the total time of the gate allocated, while Şeker and Noyan [29] research focused on reducing the idle time variance. Given the shortage or absence of gate bridges, airports may provide a remote gate to the aircraft to turn around. Ding et al. [16] tried to minimise the number of ungated flights. Marinelli et al. [18] applied a meta-heuristic approach to minimise remote gate usage.
2.2. Dynamic Gate Assignment
A dynamic assignment may be required if there are flight delays, abnormal weather conditions, or mechanical failure of the aircraft. Obviously, sudden disturbances are inevitable. However, dynamic assignment will help the operators react to these events quickly. Therefore, dynamic GAP models have been studied extensively as well. Şeker and Noyan [29] applied the stochastic model and used randomness to simulate the gate assignment. Gosling [13] designed a simple expert system adapting to delays and equipment changes. Moreover, it considers constraints imposed by the availability of facilities and personnel in handling aircraft and the consequences on downstream operations of a particular assignment decision. Lim and Wang [25] minimised the sum of delay penalties and the total walking distance. Some of the past researchers have applied GAP to solve the scheduling problem. Wang [21] employed GAP to maximise the sum of all products of the flight eigenvalue and the gate eigenvalue that the flight assigned. Gate idle time is the slack time between two successive instances of gate usage. Zhao and Cheng [17] attempted to minimise the gate buffer time. Bolat [30] applied quadratic mixed binary programming to solve GAP, with the aim of minimising the variance of idle time.
2.3. Methodologies for Solving GAP
GAP Methodology is classified into different categories: the exact algorithms to obtain the exact optimal solution for the problem, whereas the non-exact algorithms include heuristics and meta-heuristics. They aim to find out a relatively optimal solution within a reasonable time. This approach is very suitable for a huge scale problem like GAP. The optimal solution may be found out, as heuristics often gives the local optimal result only. Metaheuristics allows systematic rules and avoids the problems of the local optimum [16, 18, 24].
Exact algorithms would try to run all the possibilities. They are suitable for solving a less complex problem. The advantage of using exact algorithms is to guarantee a global optimum, which is useful when extremely high precision is needed. However, the drawback here is that the solving time is quite long. Integer Linear Programming (IP) solves the optimal solution for linear objective function and constraints. Ding et al. [31] and Ding et al. [16] applied IP to deal with static gate assignment in order to minimise the travel time, walking distance and the consequences of flight delay. Diepen et al. [32] studied GAP at the Amsterdam Airport using IP, with the goal of minimising the cost of gate planning. Binary Integer Programming (BIP) consists of IP with only binary decision variables. Yan et al. [33] considered static gate assignment a BIP. The flight delays at static gates are studied through stochastic algorithms and a case study is demonstrated based on Chiang Kai-Shek Airport. Yan and Tang [24] developed a gate reassignment framework with BIP using systematic software and worked on the same airport to reduce the cost of aircraft towing and minimise gate rest time.
Mixed-integer linear programming (MILP) allows some decision variables to integer. Bolat [34] formulated the GAP problem using MILP with the main goal of minimising the idle time between two successive utilisations of the same gate. Bolat [30] and Bolat [12] used MILP to minimise the overall variance and the range of gate idle time at Riyadh, Saudi Arabia’s King Khalid International Airport. Quadratic programming is used to optimise the quadratic objective function subject to linear constraints on these variables. Quadratic programming can be integrated with BIP as well. Zheng et al. [35] suggested a mixed binary quadratic problem for GAP to minimise the overall slack time variance. Robust linear programming considers the uncertainty in data. Narciso and Piera [22] applied robust linear programming to GAP to minimise delay and maximise gate utilisation.
Heuristic algorithms aim to provide a reasonable solution, although the solution may eventually not be the best. There are different approaches under heuristic algorithms applied to GAP, including heuristic approach, memetic algorithms, greedy algorithm and bundle algorithm. Mangoubi and Mathaisel [15] applied a heuristic approach to solve GAP at Toronto Pearson International Airport. Bolat [30] used King Khalid International Airport as a case study with heuristics. Haghani and Chen [27] attempted a heuristic approach on GAP to minimise the total passenger walking distance. A memetic algorithm is a synergy of evolutionary and population-based approaches, with separate individual learning or local improvement procedures. Lim and Wang [25] applied a memetic algorithm to solve GAP to minimise the travellers’ walking distance. A greedy algorithm is another heuristic method to solve the problem. It helps the system to find an initial feasible solution quickly. Ding et al. [16] applied the greedy approach with Tabu search to reduce the number of ungated flights and minimise the passengers’ total walking distance. The bundle algorithm is one of the traditional algorithms to solve the problem by setting a set of bundle constraints. It can ensure that the solution would not violate the constraints of GAP. Yan and Chang [36] applied the bundle algorithm to solve GAP and ensure that only one flight would be allocated to one gate at a particular time. The model aimed to assist airport managements to schedule the gate assignment effectively and efficiently. Thengvall et al. [37] applied the bundle algorithm to schedule flight recovery if the airport is closed.
There are different approaches under meta-heuristic algorithms used in GAP, including Tabu search (TS), simulated annealing (SA), genetic algorithms, ant colony optimisation algorithm, artificial bee colony optimisation, swarm intelligence, and particle swarm optimisation algorithm. TS is a meta-heuristic local search algorithm. TS applies local research from the current basic feasible solution to the neighbourhood better solution. TS first found a local solution based on the rules of the algorithm. Tabu means prohibitions, and it does not allow repeating the search of the last result. Ding et al. [16] attempted to use TS to minimise the number of remote gates and reduce the gate connection times. Lim and Wang [25] applied TS to solve GAP to minimise travellers’ walking distance. Şeker and Noyan [29] reduced the gate conflict with TS. SA applies the random search technique for global optimisation. SA simulates the effect of heating and cooling and is related to internal energy. Slow cooling in SA is a slight decrease in the probability of accepting worse solutions as it explores the solution space. Ding et al. [31] applied SA and hybrid SA to minimise the number of ungated flights and reduce the total walking distances or connection time. Dorndorf et al. [38] and Drexl and Nikulin [39] attempted to use Pareto SA to deal with multi-quadratic GAP.
Genetic algorithms (GA) were among the meta-heuristics algorithms used to solve GAP. Yang [40] illustrated that GA could provide the optimisation result or solve the problem with biological views. The advantage of GA is its ability to handle complex problems and parallelism. GA provided a solution search in which it would have a set of parent solutions for the result, then it would reproduce and provide offspring solutions based on the features of the parent solutions. Cheng et al. [41] adopted hybrid GA and TS to simulate the problem at Seoul Incheon International Airport Bolat [12] applied GA to static aircraft gate assignment to minimise the variance of idle time.
Swarm intelligence (SI) is the state-of-the-art meta-heuristics research area. The well-known SI algorithms include the ant colony optimisation algorithm (ACO), artificial bee colony (ABC) algorithm and particle swarm optimisation (PSO) algorithm. ACO attempts to simulate the behaviour of an ant colony in finding optimal/near-optimal paths. Zhao and Cheng [17] attempted ACO on GAP to minimise the gate buffer time. ABC aims to find the optimal path based on the intelligent foraging behaviour of honey bees. Marinelli et al. [18] applied the ABC method to GAP, which aims at minimisation of passengers’ total walking distance and remote gate usage. Zhang et al. [42] applied the PSO algorithm to minimise the average taxi time and improve gate arrangement in an airport. Population-based SI has the advantage of enumerating a set of solution candidates in solving an optimisation problem.
In our study, we aimed to investigate the total travelling cost of business class passengers. This is different from the past research, with their objectives focusing on time-saving and efficiency of the gates and minimising the passengers’ and ground staff’s walking distance. Although business class travellers are among the more profitable customers for airlines and airports, the previous studies of GAP seldom address the needs of this customer group. Business class travellers include frequent flyers and passengers travelling business or first class. Those passengers would be sensitive to time and the walking distances from the check-in counter, CIQ, lounge and duty-free shop to the gate. By reducing the walking time and distance, we expected that the business class passengers’ satisfaction would be increased. Meanwhile, this group of passengers may generate extra profit for the airport and the airline, including the duty-free shops, dining and purchase of souvenirs.
3. METHODOLOGY
3.1. Problem Formulation
In the GAP, we assumed the flight arrival time and departure time according to the historical data of certain flights. The departure time and arrival time of flights were collected from the historical flight data and buffer time also was considered in the proposed model. Those assumptions could be favourable for a static gate assignment in hedging delay risk. We also considered some basic rules of the GAP from the literature. Yang [40] has mentioned that one gate only serves one flight at a time, and a gate can only handle an aircraft of a certain size. According to safety regulations in different countries, a gate can only serve flights for certain destinations or origins. Furthermore, two jumbo jets cannot be assigned at two adjacent gates at the same time. Bouras et al. [43] suggested that the timetable of a flight must also satisfy the geographic constraints and business environment.
Parameters and variables are introduced in Table 2. Equation 2 is the objective function to minimise the total travelling cost. For Equation 3, it is ensured that one gate only serves one flight at a certain time. This means it avoids overlapping; that is, using the same gate for two or more aircrafts. If the gate is assigned to one flight only and would not be used by other flights, this equation must equal 0 and the equation holds. Table 3 shows the three scenarios of one flight being used at the gate. The later flight
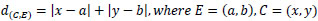 |
(1) |
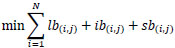 |
(2) |
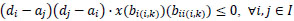 |
(3) |
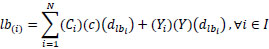 |
(4) |
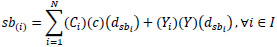 |
(5) |
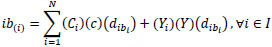 |
(6) |
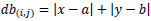 |
(7) |
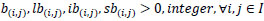 |
(8) |
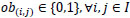 |
(9) |
3.2. System Architecture of Evolutionary Algorithm
Evolutionary algorithm (EA) was introduced by Fogel et al. [44] and further developed by Angeline et al. [45]. The objective of the EA is to create a successful crossover and mutations. The EA enables the prediction of future events based on past statistics and observations. EA is one of the meta-heuristic methods. The common idea behind these algorithms is the evolution of species based on natural selection.
3.2.1. Installation
The direction of implementing meta-heuristics for solving GAP would be applying GA to the GAP with two objectives minimise the business class travellers’ walking distance. The model would involve initialisation, selection and genetic operation which consists of recombination and mutation of the data. GA could find a feasible solution quicker with less operation time to find out the near-optimal solution. The installation in EA involves inputting the current airport gate plan into the system. The system can then formulate the solution and further improve the result through EA.
3.2.2. Operators Selection
The parent solution would be rated by a fitness value which is the attractiveness of that parent solution. The future offspring solutions generated from that parent solution would also be awarded that fitness value. The solution with the highest fitness value is more likely to be selected as a candidate for a parent solution in order to retain the candidates with the best fitness values.
3.2.3. Genetic Operators
The offspring produced from the selected parent pool proceeded to two genetic operators, which are crossover and mutation. For crossover, new offspring created from the mating of a two-parent solution is put into the next generation of the population. By recombining portions of good individuals, this process is likely to create even better individuals. Mutation induces a random walk through the search space and maintains the diversity of the solution population.
3.2.4. Termination
The operation would be terminated when the condition is reached and the objective and constraints are satisfied. The duration of the operation depends on the complexity of the program. It would be set up with a deadline to stop the operation because the GAP requires real-time and short-time results.
3.3. An Evolutionary Algorithm in the Gate Assignment Problem
The proposed method is simple which installs the current flight plan and gate slot for the specific airport. Then, we evaluate the score of the current result. Then it would perform the steps of the EA programming, and the model would select the parent solution of the gate assignment. It would process the recombination and mutation from different pairs of parent solutions and generate offspring. The iterations will be executed until the stop condition is achieved.
| Gate | CI62 | CI2161 | AK208 | PR896 | CI922 | CI911 | VN576 | CI159 | 3K723 | KE691 | CI702 | MH366 | 3K724 | TS201 | D7372 | CI680 | CI782 | CI834 | CS3095 | CI910 | TR2966 | CI7916 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| A2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| A3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| A4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A5 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| A6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| A8 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| A9 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
4. RESULTS AND DISCUSSION
In the numerical study, we adopted Taipei Taoyuan International Airport as an example to illustrate the model and method. We used the Microsoft Excel 2016 Solver – Evolutionary Engine as a medium to perform the formulation in evolutionary programming.
4.1. Description of the Test Instances
Taiwan Taoyuan International Airport (International Air Transport Association (IATA) code: TPE; International Civil Aviation Organization (ICAO) code: RCTP) is one of the two international airports in Taipei, the capital city of Taiwan. From the Taiwan Airport Corporation (TTIA) statistics, TPE is also the largest international airport in Taipei and the gateway to Taiwan. The airport is not located in the centre of Taipei City. It is located 40 km west of Taipei in Dayuan District, Taoyuan City, Taiwan. The airport was opened in 1979 and only for commercial aviation use. The former name is Chiang Kai-shek International Airport. The airport has two airport terminals and 38 boarding gates for passengers. The current capacity of the airport is 38 million passengers annually.
TPE currently serves 162 destinations in 31 countries. Those destinations are served by 73 airlines. According to the Civil Aeronautics Administration, Taiwan (CAA) statistics, TPE transports a total of 38 million passengers and 2 million tons of cargo. ACI data show that it was the 11th busiest international airport. The airport has already reached its initial capacity. TPE airport serves as a hub-and-spoke airport for Taiwan’s two main Airlines, China Airline and EVA Air. TPE has targeted becoming the gateway to the Asia-pacific region as well. TPE has the potential for enhancing business class travel. TPE has more than 10 lounges, of which three are paid lounges. The maximum capacity has been reached, and the future expansion is still at the design stage. A GAP will be useful for the TPE airport to maintain high and sufficient service quality for both business and other passengers.
The EAGAP control parameter settings are as follows:
- The mutation rate is 0.075. The population size is 80.
- The maximum number of iterations is 1000.
- The maximum time of solution without improvement is 300s.
4.2. Data Collection
After the completion of the system modelling, it will perform the feasible system test applied in the real case. This project chose the nearest airport—Taipei Taoyuan International Airport. This airport’s gate data was collected via FlightStat.com. The duration of the data collection period was 21 days. The airport's aircraft timetable usually was scheduled weekly. The collection period was from 26th September to 9th October 2015. The data collected covered 24 hours’ flight data of the arrival and departure of both passenger and cargo flights. The data included: flight number, origin and designation, aircraft type (passenger or cargo), service class, planned departure and arrival time, actual departure and arrival time, departure terminal and gate, arrival terminal and gate, and aircraft model type. The walking distances between the boarding gate and the lounge and CIQ were also measured using the floor plan provided by the TPE airport. The lounges are located in the 4/F section of the terminal. There are several lounges which serve different business passengers for different airlines. We would take the average distance for the calculation of the distance between the gate and the lounge. The distance calculation method would be based on the rectilinear distance. It would be precise, to calculate the actual walking distance for the passengers.
4.3. Data Modification and Selection
In this research, we chose terminal 1 for the analysis. Terminal 1 has 18 boarding gates from A1 to A9 and B1 to B9, where A series gates are located on the north side of Terminal 1 and B gates are located on the south side. Terminal 2 is located westward of Terminal 1, having a similar structure and pattern. It has 20 gates, from C1–C10 and D1–D10. In the data, the number of passengers on board on each flight was not provided. Therefore, this research assumed that the aircraft is 100% loaded and the seat configuration for each flight would be according to their flight type and the responding airlines. TPE Terminal 1 Gate Layout has A10–11 and B10 and B1R gates; it also has a remote gate for smaller aircraft. However, we did not include it in this model as we only considered the flights that board using the gate bridge.
4.4. Results of Experiments
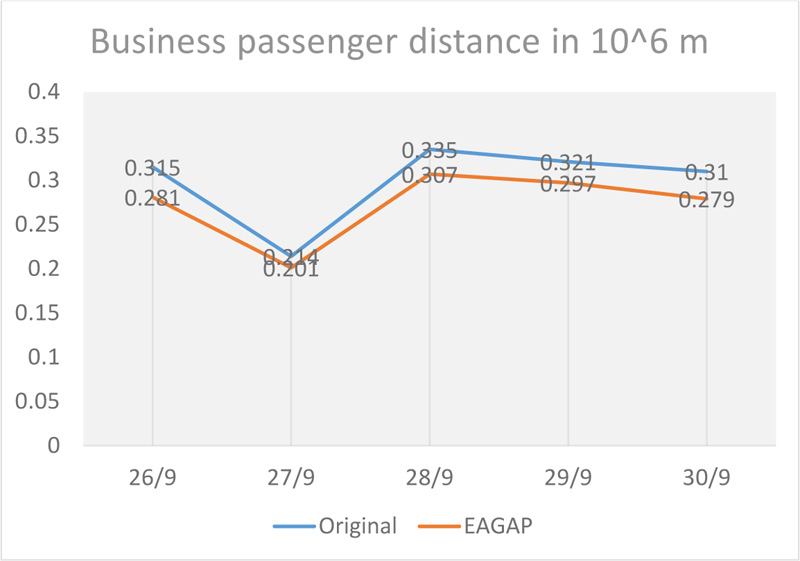
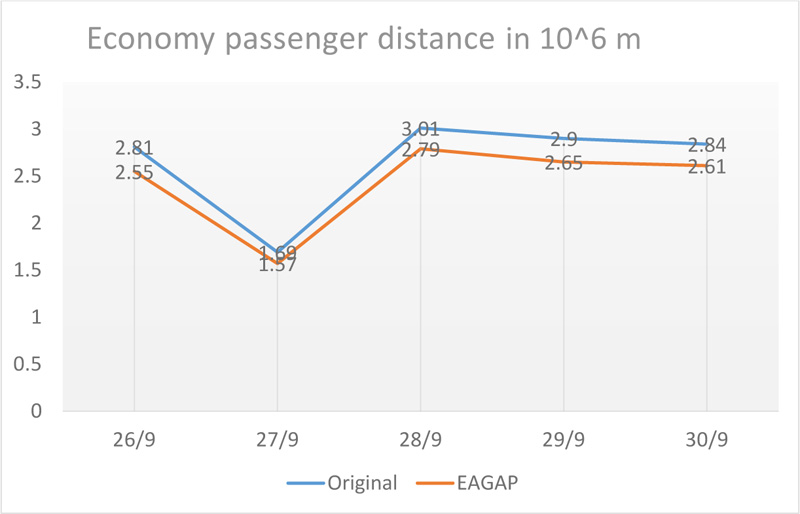
We studied the current GAP in TPE from 26/9/2015–20/9/2015, during which there was no public holiday in Taiwan. The flight pattern and airport slots could be based on the normal daily gate assignment. It would be more realistic for a pre-assigned static GAP for the airport. The study time was 0600–1700 hrs every day, which had around 17–27 aircraft successfully arriving and departing in T1 at TPE Airport. We compared the original plan with the suggested GAP model and discovered that there is improvement in the total walking distance. The walking distance for business class travellers reduced by 8.7% in total. For the economy passengers it also shows a 7.4% reduction in the walking distance, as shown in Table 4 and Figs. (1 and 2). The proposed GAP model also reveals an improvement for both economy class and business class. The results of total score are lower than the original settings. The sensitivity analysis generated by the Excel Solver was checked for the restrictions imposed on the problem. The GAP model does not accept the degenerated solutions as optimal.
| Original | Proposed GAP | |||||
| Date/(m) | Bus Class | Econ Class | Total Score | Bus Class | Econ Class | Total Score |
| 926 | 315153.44 | 2819723.32 | 3765183.64 | 280767.4 | 2554378.23 | 3396680.43 |
| 927 | 213928.32 | 1693096.52 | 2334881.48 | 201119.6 | 1565472.81 | 2168831.61 |
| 928 | 334674.01 | 3012830.7 | 4016852.73 | 306807.64 | 2787682.55 | 3708105.47 |
| 929 | 321244 | 2925569.54 | 3889301.54 | 297924.86 | 2651272.77 | 3545047.35 |
| 930 | 313033.9 | 2839443.33 | 3778545.03 | 279517.91 | 2615180.9 | 3453734.63 |
| G a t e |
6 : 0 0 |
6 : 3 0 |
7 : 0 0 |
7 : 3 0 |
8 : 0 0 |
8 : 3 0 |
9 : 0 0 |
9 : 3 0 |
1 0: 0 0 |
1 0 : 3 0 |
1 1 : 0 0 |
1 1 : 3 0 |
1 2 : 0 0 |
1 2 : 3 0 |
1 3 : 0 0 |
1 3 : 3 0 |
1 4 : 0 0 |
1 4 : 3 0 |
1 5 : 0 0 |
1 5 : 3 0 |
1 6 : 0 0 |
1 6 : 30 |
1 7 : 0 0 |
1 7 : 3 0 |
1 8 : 0 0 |
1 8 : 0 |
| A1 | 3K 723 | MH 366 | TR 2966 | |||||||||||||||||||||||
| A2 | VN 576 | 3K 724 | CI 7916 | |||||||||||||||||||||||
| A3 | CI 680 | |||||||||||||||||||||||||
| A4 | CI 62 | PR 896 | D7 372 | |||||||||||||||||||||||
| A5 | CI 2161 | CI 922 | KE 691 | TS 201 | CI 834 | |||||||||||||||||||||
| A6 | ||||||||||||||||||||||||||
| A7 | CI 159 | CI 910 | ||||||||||||||||||||||||
| A8 | AK 208 | CI702 | CS 3095 | |||||||||||||||||||||||
| A9 | CI 911 | CI 782 | ||||||||||||||||||||||||
| G a t e |
6 : 0 0 |
6 : 3 0 |
7 : 0 0 |
7 : 3 0 |
8 : 0 0 |
8 : 3 0 |
9 : 0 0 |
9 : 3 0 |
1 0 : 0 0 |
1 0 : 3 0 |
1 1 : 0 0 |
1 1 : 3 0 |
1 2 : 0 0 |
1 2 : 3 0 |
1 3 : 0 0 |
1 3 : 3 0 |
1 4 : 0 0 |
1 4 : 3 0 |
1 5 : 0 0 |
1 5 : 3 0 |
1 6 : 0 0 |
1 6 : 3 0 |
1 7 : 0 0 |
1 7 : 3 0 |
1 8 : 0 0 |
1 8 : 3 0 |
| A1 | ||||||||||||||||||||||||||
| A2 | 3K 723 | TR 2966 | ||||||||||||||||||||||||
| A3 | VN 576 | CI 680 | ||||||||||||||||||||||||
| A4 | PR 896 | CI702 | ||||||||||||||||||||||||
| A5 | CI 2161 | CI 911 | 3K 724 | CI 910 | ||||||||||||||||||||||
| A6 | CI 62 | CI 922 | KE 691 | TS 201 | CI 834 | |||||||||||||||||||||
| A7 | AK 208 | CI 159 | D7 372 | CI 7916 | ||||||||||||||||||||||
| A8 | MH 366 | CI 782 | ||||||||||||||||||||||||
| A9 | CS 3095 | |||||||||||||||||||||||||
We can observe from Tables 5 and 6 similar gate patterns as the gate capacity in TPE has reached its limit. The original plan did not assign any flights to Gate A6 which was the nearest gate to the departure hall. So, the suggested gate plan was implemented almost fully utilising Gate A6, in which 5 flights were assigned to that gate. The gates A5 and A7 have also seen massive use as they are closer to the main terminal. The new plan has greatly reduced the usage of the far gates, including gates A1, A2, A8 and A9.
CONCLUDING REMARKS
A metropolitan airport usually handles operations of more than fifty boarding gates and hundreds of flights every day. GAP can help in assigning the gates to the flights more effectively. With the advancement of genetic algorithms, the GAP model has performed a successful assignment solution within an acceptable timeframe. The proposed method could reduce the business class passengers’ total walking distances. The arriving aircraft would be allocated to the centre gate near the immigration hall, shop and airline lounges. One limitation of the current research is that the estimation of departure and arrival times was based on the data collected, whereas, in reality, other parameters, including the duration of an aircraft’s presence at the gate, weather conditions, ground staff and crews’ operation times and uncertainties may affect the solution’s robustness. The proposed GAP is only for the static pre-assigned gate approach and is not able to solve the dynamic GAP. Therefore, future research should consider the uncertain onboarding and deboarding times of passengers and other dynamic factors to cater to their impact on gate assignment, with different commercial optimisation solvers for comparison. Business passengers’ behaviour and preferences may also affect the profitability of the airport and airlines’ extra revenue. Studying passengers’ profiles and investigating the association between their purchase behaviours and the gate assignment solution may lead to a profitable solution for both airports and airlines.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
The data that support the findings of this study are available within the article.
FUNDING
None.
CONFLICT OF INTEREST
Dr. Kam K.H. NG is the Associate Editorial Board Member of The Open Transportation Journal.
ACKNOWLEDGEMENTS
This work was supported by the Department of Aeronautical and Aviation Engineering, Department of Industrial and Systems Engineering, and Division of Business and Hospitality Management, College of Professional and Continuing Education, The Hong Kong Polytechnic University, Hong Kong SAR, China. We are also grateful to the Research Committee and the Department of Aeronautical and Aviation Engineering, The Hong Kong Polytechnic University, for support to the project (UALL, BE3V). The authors would like to express their appreciation of the Taiwan Taipei International Airport and FlightGlobal’s assistance with the data collection.


