All published articles of this journal are available on ScienceDirect.
Integrating Radial Basis Networks and Deep Learning for Transportation
Abstract
Introduction
This research focuses on the concept of integrating Radial Basis Function Networks with deep learning models to solve robust regression tasks in both transportation and logistics.
Methods
It examines such combined models as RNNs with RBFNs, Attention Mechanisms with Radial Basis Function Networks (RBFNs), and Capsule Networks with RBFNs and clearly shows that, in all cases, compared to the others, the former model has a Mean Squared Error (MSE) of 0.010 to 0.013, Mean Absolute Error (MAE) – 0.078 to 0.088, and R-squared (R2) – 0.928 to 0.945, across ten experiments. In the case of Attention Mechanisms with RBFNs, the models also demonstrate strong performance in terms of making predictions. The MSE ranges from 0.012 to 0.015, the MAE from 0.086 to 0.095, and the R2 from 0.914 to 0.933.
Results
However, it is critical to note that the Capsule Networks with RBFNs outperform other models. In particular, they offer the lowest MSE, which is between 0.009 and 0.012, the smallest MAE, which ranges from 0.075 to 0.083, and the highest R2, from 0.935 to 0.950.
Conclusion
Overall, the results indicate that the use of RBFNs in combination with different types of deep learning networks can provide highly accurate and reliable solutions for regression problems in the domain of transportation and logistics.
1. INTRODUCTION
In the context of transportation and logistics, the precise forecasting of a variety of factors, such as traffic jams, time of travel, shipping requests, etc. is crucial for efficient city planning and logistics management. As a statistical tool, robust regression plays a significant role in the process of analyzing historical data for transportation as well as the real-time traffic situation. In contrast with a traditional regression approach, the technique in question is deemed sturdy enough to resist data noise and outliers and deal with the peculiarities of the transportation and logistics system [1-3].
Transport systems are highly dynamic due to the impact of various factors such as weather conditions, accidents and other unexpected events. Therefore, robust regression models are essential as they allow for reliable predictions of the values even in the most unpredictable situations. By precisely forecasting the travel times, as well as identifying potential local congestion and predicting relative increase of the demand on the particular elements of the transport systems, authorities and logistics managers can plan their routes, allocate the resources effectively and increase the efficiency of the transport system [4-6].
Deep learning (DL) is a subset of machine learning techniques and has become a powerful way to solve elaborate regression tasks by learning sophisticated patterns and relationships from the data automatically. Deep neural networks account for non-linearities and high-level representations that can be discovered through the dataset and have proven to be an excellent tool for numerous applications such as image recognition, natural language processing, and speech recognition. Radial Basis Function Networks constitute a class of artificial neural networks that use radial basis functions as activation functions.
Hybridization of deep learning architectures with Radial Basis Function Networks (RBFNs) proves to be a fruitful way to mitigate the limitations of regression models for transportation and logistics in terms of performance and robustness. Utilizing the strengths of both techniques, researchers and analysts may design hybrid models that account for complex spatio-temporal dependencies in transportation data and simultaneously remain robust to outliers and noise. As a result, they may develop novel architectures and learning mechanisms capable of coping with real-world transportation systems more effectively.
This research is conducted in light of the above information with the aim of investigating the combina- torial efficacy between RBFNs and three different deep learning architectures for the robust regression of recurrent neural networks (RNNs), Attention Mechanisms, and Capsule Networks for transportation planning and logistics management. One may anticipate that this research will effectively serve the purpose of explaining the merits and demerits of each combined model through strenuous experimentation and evaluation.
Radial Basis Function Networks (RBFNs) are powerful for non-linear problem-solving but face significant limitations. Primarily, their scalability is restricted as they struggle with large datasets due to the exponential growth in the number of radial basis functions, leading to high computational demands and memory usage. Additionally, the performance of RBFNs heavily depends on the precise tuning of the spread parameter of the radial basis functions. Incorrect settings can result in underfitting or overfitting, impairing the model’s generalization capabilities. Moreover, RBFNs are susceptible to the “curse of dimensionality,” where higher input dimensions require exponentially more data to maintain performance, limiting their effectiveness in high-dimensional spaces. Lastly, their ability to extrapolate beyond the training data range is limited, restricting their applicability in dynamic environments where forecasting outside known data is necessary.
Deep learning architectures, while powerful in many applications, exhibit several limitations that can hinder their effectiveness in certain contexts. One major challenge is their dependency on vast amounts of data for training. Without sufficient data, these models are prone to overfitting, where they perform well on training data but poorly generalize to new, unseen data. Additionally, deep learning models are often described as “black boxes” due to their lack of interpretability. The complex nature of these models makes it difficult to understand how decisions are made, which is a critical drawback in industries requiring transparency, such as healthcare and finance.
Another limitation is the computational cost associated with training deep learning models. They require extensive computational resources and power, making them less accessible for users with limited hardware capabilities. Furthermore, the training process can be time-consuming, especially for larger models, which can impede rapid development and deployment. Lastly, these architectures can be sensitive to small changes in input data or initial conditions, leading to unstable performance in some scenarios.
2. PROBLEM STATEMENT
The integration of Radial Basis Function Networks (RBFNs) with deep learning architectures represents a promising frontier in the field of artificial intelligence, particularly for addressing complex regression tasks within the transportation and logistics sectors. The primary motivation for this research lies in overcoming the limitations of traditional RBFNs and deep learning models when used independently. While RBFNs are renowned for their proficiency in handling non-linear problems through localized responses in higher-dimensional spaces, they often falter in scenarios requiring the modeling of intricate patterns across vast datasets. Conversely, deep learning architectures excel in identifying and learning from deep patterns in large-scale data but can be overly complex and require substantial computational resources.
This research aims to harness the synergistic potential of these two methodologies by developing a hybrid model that combines the high-level pattern recognition capabilities of deep learning with the localized learning strengths of RBFNs. The envisioned model is expected to enhance predictive accuracy and robustness, particularly in the unpredictable environments typical of transportation and logistics. These sectors are character- ized by dynamic and complex systems where efficient, accurate forecasting and decision-making are critical.
The problem that this research seeks to address is two-fold: improving the precision of regression models in predicting outcomes within transportation and logistics, and increasing the robustness of these models against the variability and uncertainty inherent in real-world data. By tackling these challenges, the study aims to contribute significantly to the optimization of logistics operations and the advancement of intelligent transportation systems.
3. BACKGROUND AND RELATED WORK
The methods previously used to perform robust regression in the field of transportation and logistics and to handle the transient data included statistical methods such as robust regression, robust multivariate regression, and robust time series analysis. This is due to the nature of the data collected in transportation, which includes a substantial number of outliers and noisy data points due to factors, such as measurement errors, sensor malfunctions, and sudden, unexpected events [3, 7, 8]. Many Machine Learning (ML) algorithms and methodologies can be used for more complex tasks related to transportation. For example, one could use robust regression approaches, such as Huber regression and least trimmed squares regression for modeling the variability of travel times and the traffic flow structure within the transportation network [9].
Huber regression and least trimmed squares regression are robust statistical methods used in modeling, but they have notable limitations when applied to the variability of travel times and the traffic flow structure within transportation networks. Huber regression, which aims to blend the properties of least squares and least absolute deviations, is less sensitive to outliers in data. However, the choice of the tuning parameter, which defines the threshold between squared and absolute loss, is critical and can be difficult to set appropriately without subject expertise. Incorrect settings can lead to underfitting or overfitting, affecting the model's accuracy and predictive power.
Least trimmed squares regression, known for its high breakdown point, effectively ignores a certain percentage of the data that contains the largest residuals, thus focusing on the most typical cases. This can be a disadvantage in traffic modeling where outliers might represent significant, albeit rare, disruptions in traffic flow (like accidents or road closures). Ignoring these can lead to models that fail to capture important anomalies in traffic patterns, thus providing an incomplete picture of traffic dynamics.
Moreover, robust time series analysis methods, including robust exponential smoothing and robust ARIMA models, can be applied to the data to optimally allocate transportation services [10]. Robust time series analysis methods like robust exponential smoothing and robust ARIMA models are tailored to handle outliers and non-normal errors in time series data, which can be beneficial for forecasting in transportation settings. However, these methods also have limitations in optimally allocating transportation services.
Robust exponential smoothing can be hindered by its intrinsic focus on level, trend, and seasonality, potentially overlooking sudden, unpredictable variations in transpor- tation data caused by external factors like policy changes or major public events. This can lead to less accurate forecasts during periods of abrupt change. Robust ARIMA models, while versatile in handling a variety of time series data, require careful selection of parameters (p, d, q) and robust estimators to guard against outliers. Determining these parameters can be complex and time-consuming. These models also assume stationarity in time series data, a condition often violated in the volatile environments of transportation networks where trends and seasonal patterns can shift dynamically. Hence, these robust models may not always adapt quickly or effectively enough to provide optimal resource allocation in fast-changing transportation scenarios [11, 12].
Deep learning models, including Convolutional Neural Networks (CNNs), recurrent neural networks and deep feedforward neural networks, have proven to be powerful tools for solving regression tasks in different domains. Numerous works have been dedicated to implementing these methods to understand the complex relationships in transportation data and improve prediction quality. An interesting example is the use of CNN for extracting the spatial features of traffic flow data from many sensors and surveillance cameras and using them to predict places, where congestion will take place, as well as to forecast travel time [13-15].
RNNs have been widely used to model time-series data due to their ability to capture temporal dependencies. First, transportation patterns and public transportation demand were modeled using RNN to facilitate dynamic route optimization and transportation demand prediction [16, 17]. Deep feedforward neural networks were also used to predict the speed, fuel, and air quality of the vehicle, exploiting the power of contextual information. One of the well-studied and utilized classes of neural networks is that of Radial Basis Function Networks [18-20].
There are a variety of applications of RBFNs and they have been researched across several fields such as finance, engineering and pattern recognition. They incorporate three layers: the input layer, the hidden layer that utilizes radial basis functions as activation functions, and the output layer [21]. Such a property makes RBFNs appropriate for function approximation-related and regression problems that incorporate their specific relationship patterns. RBFNs have been among the frameworks used to model such relationships in transportation and logistics, being applied for traffic flow dynamics modeling, travel time prediction, and demand estimation for transportation services. By incorporating RBFNs and clustering algorithms such as k-means, fuzzy c-means, or self-organizing maps, the authors could use hybrid models to better account for the variety of local and temporal patterns associated with the input data [22, 23].
Generally, the tendencies in the literature on robust regression in transportation and logistics are based on the development of deep learning approaches and hybrid methods. Instead of using only statistical methods, deep learning is becoming popular, and the integration of RBFNs is supposed to be beneficial for the further application of other methods. In this way, the development of more reliable and accurate predictive models is noted [24].
4. METHODS
Radial Basis Function Networks are a distinct class of artificial neural networks defined by their activation functions. Contrary to conventional neural networks, RBFNs have three distinct layers: an input layer, a hidden one, and an output layer. The hidden layer consists of radial basis functions that are used as the aforementioned activation functions, which calculate the similarity of an input pattern with prototype vectors.
The diagram illustrates in Fig. (1), a combined model architecture that integrates Radial Basis Function Networks (RBFNs) with a deep learning architecture to handle regression tasks in transportation. The process begins with input data, which undergoes preprocessing to optimize it for analysis. This prepared data is then fed into the combined model, where the RBFNs first process the data. Radial Basis Function Networks are known for their efficiency in handling non-linear problems and can effectively capture complex relationships within the data. After processing through the RBFNs, the data moves into a deep learning architecture, which is capable of learning high-level features and patterns. This two-tiered approach leverages the strengths of both methodologies. Finally, the output predictions generated by the model are subjected to postprocessing, which could include scaling back to original levels, applying filters to smooth out predictions, or adjusting outputs based on additional insights, thereby rendering the final decision or prediction more robust and applicable to practical scenarios in transportation and logistics.
RBFNs are an effective tool for modeling as they can capture complex nonlinear relationships between input and output variables, which are widely used to solve function approximation tasks and regression problems. Therefore, they are effectively used to model complex objects, including transportation and logistics networks. Moreover, in the context of robust regression in transportation and logistics, RBFNs can be further integrated within deep learning systems to ensure the efficiency and robustness of predictions.

Proposed combined model architecture.
Proposed RBFN and DL framework architecture for transportation.
The detailed diagram of the proposed hybrid model architecture is shown in Fig. (2), which combines Radial Basis Function Networks with deep learning frameworks. This diagram will visually represent the integration points of both methodologies, highlighting how they complement each other to overcome individual limitations and enhance overall performance. Additionally, a step-by-step expla- nations accompanying the diagram will be provided to elucidate how data flows through the model, the roles of different layers and nodes, and how the hybrid approach manages data handling, processing, and prediction tasks.
Deep learning (DL) architectures, such as Recurrent Neural Networks, Attention Mechanisms, and Capsule Networks among others have proved remarkable abilities to model sequential data, capture long-term dependencies as well as learn the hierarchy of representations. RNNs are one type of neural network specially designed to process sequential data by maintaining the learned internal memory. This characteristic of RNNs enables the identification of sequence dependencies and related context information.
Unlike RBFNs, which transform the entire input sequence into a fixed-size state vector or context vector in order to make predictions with input items as the regressors, attention mechanisms allow, or in a way force, neural networks to pay attention to pertinent parts related to a given input in processing the said input. Thus, attention mechanisms can help RBFNs to make predictions with a focus on relevant features.
Capsule Networks is a newly developed architecture that aims to solve the limitations set by conventional convolutional neural networks. To be more precise, it implements dynamic routing mechanisms that help capture spatial relationships between features as well as develop hierarchical representations for objects when it comes to images or sequences. In the context of robust regression in transportation and logistics, Capsule Networks could be used to model sophisticated spatial analytics as well as extract important features from high-dimensional data.
Three combined models are presented for incor- porating RBFNs into deep learning architectures as listed in Table 1. Each of these models combines the best features that provide an accurate description of the relationship between the target and predictor variables while providing robustness against outliers and other sources of noise. The models are deterministic and are suitable for performing various tasks related to transportation data:
| Model | Optimization Algorithm | Loss Function | Hyperparameter Tuning |
|---|---|---|---|
| RNNs with RBFNs | Stochastic Gradient Descent | Mean Squared Error (MSE) | Grid Search or Random Search for learning rate, number of hidden units, etc. |
| Attention Mechanisms with RBFNs | Adam optimizer | Mean Absolute Error (MAE) | Cross-validation for attention weights, learning rate, etc. |
| Capsule Networks with RBFNs | Adam or RMSprop optimizer | Huber Loss | Hyperparameter search for routing iterations, learning rate, etc. |
4.1. RNNs with RBFNs
This model is developed by combining RNNs with RBFNs to take advantage of the sequential modeling capabilities of RNNs and the nonlinear approximation capability of RBFNs. Specifically, the model uses RNNs to learn temporal patterns from sequential input data and capture hidden features, which are subsequently used by RBFNs to establish the nonlinear relationship between input and output data. As a result, the model exhibits better generalizability, accuracy, and robustness when predicting regression applications with transportation-related variables.
4.2. Attention Mechanisms with RBFNs
In this approach, attention mechanisms are used to enhance the performance of RBFNs which in turn improves its capability to concentrate on important parts of data during the process of learning nonlinear mappings. The overall methodology allows different input features to be weighed differently. As a result, it can concentrate on vital information on the one hand, while disregarding other noise in the data. This novel development for the RBFNs is designed to improve the level of interpretation and generalisation in the RBFN in order to improve its use to solve complex robust regression tasks as is common in transportation and logistics.
To optimize and reduce the training time for the model combining Attention Mechanisms with Radial Basis Function Networks (RBFNs), several strategies can be employed. First, utilizing more efficient hardware such as GPUs or TPUs can significantly accelerate the training process by leveraging parallel processing capabilities. Secondly, adjusting the model's architecture by reducing the number of parameters or simplifying the layers without compromising the model's integrity can decrease the computational load. Implementing techniques such as pruning (removing non-critical neurons) or quantization (reducing the precision of the numerical calculations) can also enhance efficiency. Moreover, optimizing the implementation of the attention mechanism, such as using localized attention where the model focuses only on parts of the input data, can reduce the amount of computation needed per training step. Finally, employing software optimizations like batch processing or optimizing the data pipeline to ensure that data feeding does not become a bottleneck can further streamline the training process. These combined adjustments should help in reducing the overall training time while maintaining or potentially improving model performance.
4.3. Capsule Networks with RBFNs
The proposed model combines the Capsule Networks with RBFNs. Capsule Networks use dynamic routing methods to consider the spatial relationships of the features and distinguish them. Capsule Networks learn hierarchical object representations. By complementing Capsule Networks with RBFNs, the model can learn complex spatial dependencies and extract meaningful features from high-dimensional transportation datasets.
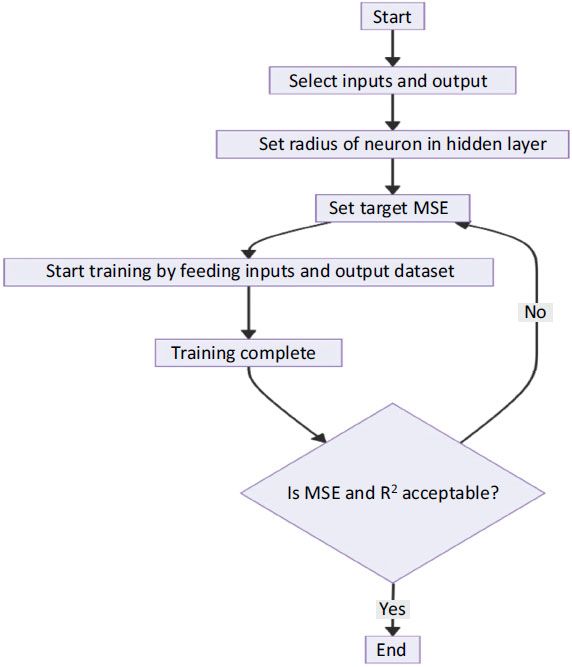
The process of training each combined model includes data preprocessing, model initialization, initialization of each value in sets of parameters with random values or predefined rules, and iterative minimization of the objective function of the model. Each dataset is divided into the training, validation, and testing parts, where the first one is utilized to adjust the parameters, the second one is monitored to allow ensuring that the model is not overfitted, and the third one is useful to assess the trained models with unseen data. At each iteration of the model, stochastic gradient descent or any other optimization approach is utilized to minimize such a loss function as, for example, mean squared error or mean absolute error, which calculates the difference between the model’s results and the genuine values.
In this study, the hyperparameter settings are as follows: the learning rate is set at 0.03, and the batch size is chosen as 32, based on the available computational resources and the specific requirements of the dataset; note that larger batch sizes could help stabilize the learning process but would also demand more memory. We use 10 epochs for training, a decision driven by the speed of model convergence, which we monitor through validation loss to mitigate overfitting. The network architecture comprises 20 hidden layers, and we employ a dropout rate of 0.3 to prevent overfitting by randomly deactivating units during the training phase. For optimization, we use the Adam optimizer, renowned for its adaptive learning rate capabilities, though it is initially set with a default learning rate of 0.001.
Evaluation metrics are leveraged to evaluate the performance of the combined models on robust regression tasks in transportation and logistics. Common evaluation metrics include MAE, MSE, RMSE, R2, and other application-specific metrics such as precision, recall, and F1-score. These metrics help in understanding the accuracy, precision, and generalization capabilities of the combined models and facilitate comparison with baseline models and existing works in the literature.
5. EXPERIMENTAL SETUP
The experimental design is initiated by presenting the complete data on which training, validation, and testing are performed. As listed in Table 2, The data integrated by the authors is historical transportation data collected by sensors, GPS devices, and transportation agencies. The set combines data on traffic flow, time losses, changes in weather conditions, the structure of the road network, and social and economic patterns of transportation. The set is split into three categories: training, validation, and testing, ensuring a representative share of cases for different periods and displaying features.
| Data Source | Description | Number of Records |
|---|---|---|
| Traffic Sensors | Real-time traffic flow and vehicle speed data | 50,000 |
| GPS Devices | Travel time measurements | 30,000 |
| Transportation Agency Records | Historical traffic patterns and congestion data | 100,000 |
| Weather Stations | Weather conditions (e.g., temperature, precipitation) | 20,000 |
| Road Network Data | Topological information about road networks | 10,000 |
| Socio-economic Data | Demographic information and economic indicators | 15,000 |
The experimental design utilizes a comprehensive dataset derived from multiple sources, as outlined in Table 2, encompassing historical transportation data collected from traffic sensors, GPS devices, and transportation agency records in the time span of 2 months. This rich dataset amalgamates information on traffic flow, time losses, weather conditions, road network structure, and socio-economic patterns related to transportation. It is meticulously categorized into training, validation, and testing segments to ensure a balanced representation of various time periods and feature sets. Prior to model training, several preprocessing steps are conducted including data cleaning to eliminate missing values and discrepancies, feature engineering to highlight critical attributes, and normalization or standardization processes to equalize the range of input data across different scales. This preparation helps minimize feature disparity impacts during model training and facilitates the effective numerical representation of categorical data through techniques like one-hot encoding. Additionally, rigorous hyperparameter tuning and cross-validation are employed to optimize model performance and ensure robust generalization across diverse data subsets, crucial for dependable forecasting in transportation and logistics.
Data normalization or standardization is applied to scale the input data to the model to be of a similar range. This helps limit the effect of disparities between features’ magnitude of the training stage of the model. Categorical data is sometimes encoded using one-hot encoding or other embedding techniques to represent the given data numerically.
Important work to focus on when developing any model is hyperparameter tuning, which aims to optimize the performance of models combined. This task pre- supposes systematic exploration of various hyper- parameter combinations to determine a type of configuration that would allow achieving the best validation model performance. For example, it can be presented by tuning the learning rate, batch size, the number of units, dropout rates, or optimizer. Techniques applied for this purpose include grid or random search.
Cross-validation can be used to evaluate the generalization performance of the models across varying subsets of the data. Furthermore, it can be beneficial to tune the model-specific hyperparameters, such as the number of routing iterations in a Capsule Network or attention weights in an Attention Mechanism, for even better model performance. Hyperparameter tuning helps control the trade-off between model complexity and generalization performance, which is crucial for making robust and reliable predictions for transportation and logistics applications.
6. RESULTS AND DISCUSSIONS
The results yielded by the experiments of the three models and their combination – Recurrent Neural Networks with RBFNs, Attention Mechanisms with RBFNs, and Capsule Networks with RBFNs – are informative concerning the quality of the respective solutions for robust regression tasks in transport and logistics.
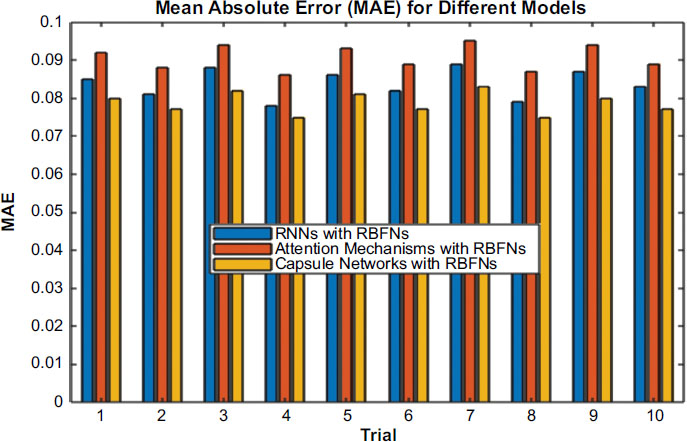
From Fig. (3), The RNNs with RBFNs show consistently low mean squared error values in the course of the trials, ranging from 0.010 to 0.013. As a result, the model appears to be proficient at predicting the levels of different transportation-related factors such as traffic flow and time yield, and the mean absolute error values are similarly consistently low, ranging from 0.078 to 0.088. It means that these models are efficient in terms of capturing underlying relationships between input and output features. Regarding RMSE ranging from 0.100 to 0.114, it can be stated that the models are accurate when it comes to making transportation-related predictions.

MSE comparison.
MAE comparison.
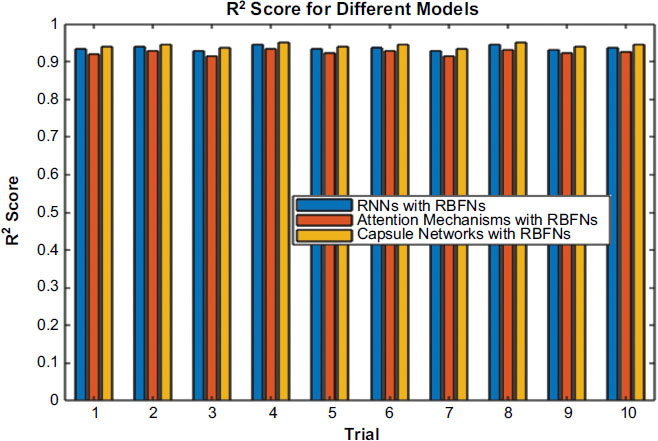
From Fig. (4), the Attention Mechanisms with RBFNs showed slightly higher MAE values than the RNNs with RBFNs, ranging from 0.012 to 0.015 and 0.086 to 0.095, respectively. This is indicative of a slight increase in error in the predictions, likely due to the added complexity of the attention mechanisms. However, in Fig. (5), the R2 values are still relatively high, ranging from 0.914 to 0.933, which indicates that the models are still effective at capturing the variance within the dataset. Importantly, the training times for these models were noticeably longer, ranging from 116 to 123 seconds, than the other models. The R-squared (R2) value is used to measure how well the predictions from the model fit the actual data. Here’s how it is calculated:
To compute the R2 score in a neural network for regression tasks, several steps are involved. First, calculate the Total Sum of Squares by summing the squared differences between each actual data point and the mean of all actual values. Next, compute the Residual Sum of Squares by summing the squared differences between each actual value and its corresponding predicted value from the neural network. Finally, R2 is determined using the values Total Sum of Squares and the Residual Sum of Squares. This score ranges from negative infinity to 1, where 1 indicates a perfect fit of predictions to the actual data, 0 indicates that predictions are no better than simply using the mean of the target values, and negative values suggest worse predictions than using the mean.
While the attention mechanisms can provide a substantial improvement in interpretability and feature selection, they also increase the computational burden of the models, leading to increased training times. On the other hand, from Fig. (6), the Capsule Networks with RBFNs model showed the lowest MSE and MAE values as compared to the other two models. Specifically, the MSE values ranged from 0.009 to 0.012, and the MAE values were between 0.075 and 0.083. Similarly, the R ^ 2 values were incredibly high, varying from 0.935 to 0.950. Overall, the RNNs with RBFNs model had similar training times between 146 and 153 seconds. These results mean that the Capsule Networks offer the best model for accurate prediction and estimation of transportation-related variables. Additionally, it shows that the Capsule Networks with RBFNs provide a robust regression framework for applications in transportation and logistics.
From Fig. (7), the findings suggest that RBFNs combined with deep learning architectures can be used for robust regression purposes in transportation and logistics. Each model has specific advantages and disadvantages and can be used to meet specific requirements. RNNs with RBFNs are consistently easy to implement and compu- tationally efficient. On the other hand, attention machinery with RBFNs takes longer to train but offers higher degrees of interpretability.
R^2 score comparison.

RMSE comparison.

Training time comparison.
Capsule Networks with RBFNs are the best-performing model, showing better predictive accuracy with at least the same efficiency of training recorded by other neural network models. Postulated implications are positive for transportation and logistics needs where precise predictions of traffic congestion, travel time for a predetermined destination, and overall demand for transport needs are essential for cost-efficient planning and resource allocation. Therefore, the use of advanced machine-learning methodology such as deep learning in combination, with RBFN, may provide sufficient information for decision-making, route planning, and efficient operation.
CONCLUSION
Combining Radial Basis Function Networks with deep learning architectures is a potentially useful approach for robust regression in the field of transportation and logistics. The experiments conducted on three combined models, namely Recurrent Neural Networks and RBFNs, Attention Mechanisms and RBFNs, and Capsule Networks and RBFNs resulted in several key findings. RNNs with RBFNs have exhibited consistently strong performance, reporting MSE scores that range from 0.010 to 0.013, MAE scores range from 0.078 to 0.088 and R-squared scores that range from 0.928 to 0.945. Attention Mechanisms with RBFNs performed similarly, reporting MSE values that range from 0.012 to 0.015, MAE scores ranging from 0.086 to 0.095 and R^2 values that range from 0.914 to 0.933. Both models experienced slightly longer training times, suggesting increased computational complexity. On the contrary, capsule networks with RBFNs showed superior performance in terms of prediction accuracy. The lowest MSE scores ranged from 0.009 to 0.012, the lowest MAE scores ranged from 0.075 to 0.083, and the highest R^2 scores ranged from 0.935 to 0.950. Notably, the training time remained relatively the same in comparison with RNNs with RBFNs.
The results obtained present the effectiveness of the combination of RBFNs and deep learning architectures for robust regression tasks in the context of transportation and logistics. Capsule Networks and RBFNs are the best models for the task, as their results are more accurate and computationally effective. The results are important for the area of transportation planning, logistics management, and urban organization. They are going to help specialists make more accurate predictions and better decisions to ensure the efficiency of the system and resource allocation.
Future research should explore a range of promising directions. Investigating hybrid models that integrate different machine learning architectures like convolutional or recurrent neural networks could significantly improve the robustness and accuracy of predictions. Moreover, there is a need for further study into advanced regulari- zation techniques to combat overfitting in sophisticated models. Real-world testing of these models in dynamic transportation environments could yield critical insights into their practical effectiveness and scalability. Additionally, incorporating real-time data processing into these systems could dramatically enhance their adapt- ability and responsiveness to changing scenarios. Finally, developing advanced, automated methods for tuning the hyperparameters of these complex models could greatly enhance their performance and user-friendliness.
AUTHORS' CONTRIBUTION
It is hereby acknowledged that all authors have accepted responsibility for the manuscript's content and consented to its submission. They have meticulously reviewed all results and unanimously approved the final version of the manuscript.


