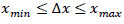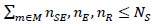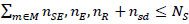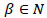All published articles of this journal are available on ScienceDirect.
A Multi-Objective Optimization of Clustered Train Delay Propagation Model
Abstract
Introduction
This research investigates train delay propagation, focusing on identifying influencing factors, optimizing parameters to minimize delays, and proposing cost-effective mitigation measures using the southern intercity railway route of Thailand as a case study.
Methods
The study employs cluster analysis and multiple linear regression to formulate delay propagation models, followed by multi-objective optimization to achieve optimal variable sets. In addition, by analyzing passenger patterns across different train types, the representative models are developed to inform policy adjustments and optimize service delivery. The research focuses on aligning commercial viability with passenger needs and preferences.
Results
Findings from this study will provide valuable insights for future planning and potential application to other rail routes. Key findings suggest that for double-track systems, effective policies include increasing train acceleration rates, adjusting the number of stops, and enhancing junction systems. For single-track systems, similar policies apply, with additional emphasis on converting to double tracks to minimize delays in train shunting.
Conclusion
Implementing these measures is expected to mitigate cumulative delays and enhance rail service efficiency.
1. INTRODUCTION
Efficient operation of railway networks is critical for the smooth and timely movement of trains. Delays in one part of the network can propagate and cause widespread disruptions, affecting the entire system. Understanding and mitigating these delays is crucial for train operators and planners to enhance the performance of railway operations. This research aims to investigate the factors that influence train delays, optimize parameters to minimize delays, and propose cost-effective mitigation measures using the Thailand national southern intercity railway network as a case study.
1.1. Background
Train delays can be classified as initial and knock-on delays. Initial delays are affected by environmental impacts, mechanical equipment failure, and human factors, while knock-on delays are caused by other delayed trains. The analysis of train delays is crucial for ensuring efficient and punctual services. Understanding the influencing factors contributing to train delays is essential for delay propagation prediction in various track layouts and circumstances, which is a foundation for network optimization to enhance service performance and quality.
2. LITERATURE REVIEW
Previous research has largely focused on modeling train delay propagation using statistical techniques. Initial studies concentrated on formulating these models, while later works have explored optimizing delay propagation for both single and multiple objective problems. However, a gap in the literature exists regarding the implementation of cost-effective measures to mitigate delay propagation [1].
2.1. Delay Propagation
A delay of a train is called a “primary delay” if it would have occurred with no other train in the network. Causes of primary delays may vary, but even the initial occurrence of a minor problem can lead to a major delay, such as the signaling of a train departing a station or the malfunction of mechanical equipment failure, human factors, and environment impacts. Sometimes trains are delayed due to a restricted running speed caused by natural disasters or bad weather [2].
A delay of a train caused by another train is called a “secondary delay” that leads to a phenomenon called delay propagation. Even when a train is delayed, the delay can be restored if there is sufficient margin (or supplement) in the running times or in the dwell times. However, if the delay is larger than the margin, the delay will remain and lead to a so-called “knock-on delay” [3].
Knock-on delays or propagation of delays to another train usually occur when there is a conflict of resources, as shown in Fig. (1) [4], such as when a train is arriving at a track (station) that is still occupied by another train, so the arrival must be delayed. When two trains use routes crossing each other at the same time, one of them must stop, as a result, the other train is delayed. With a single-track line (such as the track between stations), trains can only meet at stations, and if the arrival of a train is delayed, the departure of the opposing train will be delayed. When a train arrives late, the departure of another train to which the same train set is assigned will be delayed if the delay is larger than the margin in the turn-back time. When a train arrives late, the departure of another train to which the same driver or conductor is assigned will be delayed if the delay is larger than the margin in the time for crew transfer. Another situation that is observed very commonly is a delay propagation caused by a connection of trains, namely when a train arrives late, and the delay is not so large, the departure of the connecting train is delayed [3].
Potthoff (1970), in a study [5], provides equations to calculate propagation factors for dynamic delay propagations. The theory has been reproduced by Jernbaneverket (2015) in another research [5] in a Norwegian translation. The propagation factor on single tracks is a function of the initial delay, headway time, buffer time between trains, and the number of sections on the single track. This section provides a brief description of the equation for single tracks. The line is assumed to consist of equal sections. Delays are denoted by p and indexed by the order number in the delay propagation, such that p1 is the initial delay of the delayer train [5]. The sum of delays in a dynamic delay propagation can approximately be expressed by:
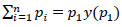 |
(1) |
With the propagation factor y(p1) given by
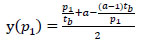 |
(2) |
where tb is the buffer time, n is the number of trains in the dynamic delay propagation and a is the number of block sections through single track, including the delayer train.
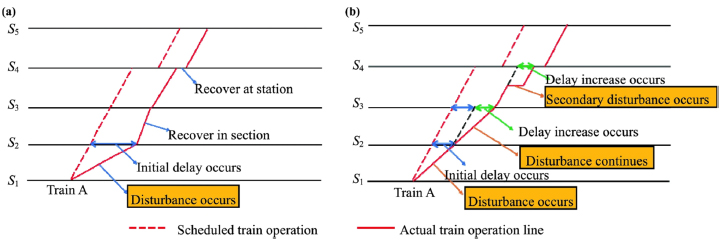
Delay increase or recovery after initial train delay: (a) process of train delay recovery; (b) process of train delay increase [4].
The equations are derived with the assumption that the initial delay is larger than the buffer time, i.e. p1 > tb. Eqs. (1-2) implies the expected values for propagation factors.
In addition, influencing factors have been mentioned from several perspectives, including operational such as planned running time, real running time, planned/real train speed and running time supplement in single/double track, number of trains, primary/knock-on delays, incidents, weather, the priority of trains, train mix, and traffic conditions [6-8]; infrastructure such as the length of single/double track and network topology [9]; and timetables such as buffer time, headway, and random arrival/departure time from the origin [2, 10, 11].
The generalization of existing classifications for train delays was proposed by Lee et al. (2016) [12]. Lee et al.'s classification includes four categories: station-related, train-related, operation-related, and timetable-related delays. These categories are designed to comprehensively cover the complete range of input information essential for train delay prediction approaches such as Historic train movements (HTM), Infrastructure information (INI), Operational information (OPI), and External factors and weather (EFW) [13].
Tiong and Palmqvist (2023) [14] highlight optimization as a key approach in addressing train delay propagation. Optimization methods, like Mixed Integer Programming (MIP) and heuristics, are employed to minimize delays, enhance capacity utilization, and fine-tune train schedules under constraints such as limited resources and conflicting train operations. These models aim to balance trade-offs like service quality versus operational costs or delay minimization versus capacity maximization. Methods like Tabu Search and Branch-and-Bound are used for timetable adjustments and real-time rescheduling to prevent knock-on delays across the network. However, a major limitation of traditional optimization models is their focus on single-objective functions, making them less adaptable to real-world complexities involving multiple competing objectives like minimizing delays, fuel consumption, and passenger inconvenience.
2.2. Optimization
Optimization is defined as the process of modifying the inputs of objective functions to search for a minimum or maximum value of output(s), mostly under limitations and constraints [15]. Optimization is a popular process that has been used in solving engineering problems. The examples of optimization techniques are simplex algorithms, genetic algorithms, simulated annealing, particle swarm, ant colony, neural network-based, and fuzzy optimization [15]. Originally, the optimization programming was executed only on one planning objective, and it has advanced to solve multi-objective problems with an increase in its potential and capabilities in suggesting more proper solutions [15]. Optimization-based methods are sometimes used to create optimal timetables that maximize capacity utilization while minimizing total network delays. The study “A Multi-Objective Optimization Model for the Intercity Railway Train Operation Plan: The Case of Beijing-Xiong 'an ICR” [16] focuses on optimizing the intercity train operation plan for sustainable development. The study constructs a multi-objective optimization model to reduce costs and travel time. A genetic algorithm is used to solve the optimization model effectively. The optimized train plan helps lower costs and save passenger travel time, promoting sustainable development of intercity railways by improving operational efficiency.
Ransikarbum et al. (2003) [17] apply k-means clustering to solve location and routing issues in the biofuel supply chain. K-means clusters biomass collection sites to facilitate efficient locational planning. It is then integrated with a multi-objective vehicle routing model that simultaneously minimizes economic, environmental, and social costs. Clustering simplifies the network, reducing complexity, and allows the multi-objective optimization model to focus on improving delivery times and cost efficiency. This combination ensures that decision-makers can balance conflicting objectives like reducing fuel consumption and meeting flexible delivery windows.
Moreover, to enhance delay propagation management in railway networks, the integration of k-means clustering with other optimization techniques, as highlighted in the hospital and biofuel supply chain studies, offers valuable strategies regarding cluster-based delay management in railway networks. K-means clustering can be used to group stations or segments with similar delay patterns, geographic proximity, or passenger volume. This segmentation allows a more localized and focused approach to delay management. For instance, high-traffic stations or segments prone to frequent delays could form a cluster where specific delay mitigation strategies, such as timetable adjustments or resource prioritization, are applied. K-means can also optimize resource allocation, which appeared in the referred medical supplies and biofuel studies [17]. For example, train crews, maintenance teams, or rolling stock could be distributed based on the characteristics of each cluster, ensuring that high-delay clusters receive more attention and resources to minimize disruptions.
2.3. Statistical Methods
Statistical models such as regression analysis or correlation analysis are widely used to understand the distribution characteristics of operational data in the context of different routes or entire rail networks. These statistical methods collect and summarize data to provide a broad or detailed picture of specific stations or trains. However, they lack specific insights into recurring delay patterns and the relationships between delays at different locations.
In addressing delay propagation in railway networks, a gap exists in fully integrating predictive clustering methods with optimization techniques. While the k-means algorithm can segment the railway network into clusters based on traffic patterns or geographical proximity, there is limited research combining clustering techniques with regression models for predictive analysis before optimization. Applying the elbow method with k-means clustering can help determine the optimal number of clusters for different regions of a railway network, enhancing the efficiency of timetable rescheduling and resource allocation.
Examples of k-means clustering applications include the integration of k-mean clustering into the capacitated vehicle routing problem (CVRP) to optimize hospital locations and distribution planning in Thailand’s healthcare system. K-means is used to group hospitals based on geographic proximity and other characteristics to determine optimal central hospital locations, acting as distribution hubs. Afterward, the CVRP model plans the distribution of medical supplies from these central hospitals to other facilities, aiming to minimize total travel distance and optimize delivery routes. The integration of k-means with GIS technology enhances the visualization and practical application of logistics planning, while sensitivity analysis refines the clustering process to improve operational efficiency [18].
The study “Statistical Estimation of Railroad Congestion Delay” [19] identifies factors causing railway congestion using statistical analysis. It predicts train running times based on factors related to congestion, focusing on specific congestion parameters of railway areas. The accuracy of congestion prediction and its effects on railway congestion are assessed by identifying factors causing railway congestion for practical forecasting. The regression results provide insights into the impact of train delays and congestion factors. The study discusses optimization methods based on simulation and parameters, using linear regression and automatic correction of continuous time regressions.
Using multiple linear regression (MLR) on historical data could predict key variables like delays or train arrivals within these clusters, offering a pre-optimization predictive framework. For instance, MLR could account for train-specific factors (e.g., train type, distance, number of stops) to estimate delays more accurately. Additionally, by combining the clustering approach with MLR, each cluster can have tailored predictions before applying more computationally expensive optimization techniques (e.g., MIP or heuristic-based algorithms), allowing for more dynamic and region-specific strategies. However, a major gap in the current literature is the lack of studies leveraging this combined K-means clustering and regression approach as a preprocessing step to enhance the performance and interpretability of subsequent multi-objective optimization in railway networks.
2.4. Problem Statement
This research aims to develop a multi-objective optimization model of clustered train delay propagation mitigation that not only minimizes the delay propagation of each cluster but also maximizes the cost-effectiveness of investments in delay mitigation measures. The model is expected to support planners and operators in the prioritization of train delay mitigation policies. The type of mathematical model developed in this research is a multi-objective linear optimization model in accordance with the following reasons:
1. Clustering of delays: First, the train delay data are clustered into different delay clusters based on the similarity in influencing factors in three perspectives (timetable, operation, and infrastructure factors). This process helps the researcher understand the inherited characteristics of each delay cluster.
2. Multiple linear regression: For each cluster or perspective, multiple linear regression is performed to illustrate the linear relationship between the independent variables or influencing factors (factors causing delays) and the dependent variable (the delay propagation).
3. Multi-objective optimization: The final step involves multi-objective optimization. This suggests that the model is trying to optimize multiple objectives simultaneously, which could include minimizing delays in each cluster while maximizing the cost-effectiveness of the option policies proposed.
Given that the regression models used are linear, and assuming the optimization constraints are also linear, the overall mathematical model can be classified as a linear multi-objective optimization model. Key characteristics of this model type:
1. Linearity: The relationships between variables are assumed to be linear.
2. Multiple objectives: The model aims to optimize several objectives simultaneously.
3. Optimization: The goal is to find the best solution that satisfies all objectives and constraints.
It is worth noting that while the individual components (regression models) are linear, the clustering step introduces a non-linear element to the overall process. However, if the final optimization is performed on the linear regression outputs with linear constraints, the core mathematical model used for decision-making would still be considered a linear multi-objective optimization model. This type of model is particularly useful in complex systems like train networks, where multiple, often conflicting, objectives need to be balanced (e.g., minimizing delays while maximizing efficiency and customer satisfaction). The summary of Literature Reviews on the Delay Propagation Model is shown in A1 in the Appendix.
3. METHOD
The framework of the research study and detailed structure of the evaluation model are shown in Fig. (2).
Furthermore, to investigate the influencing factors on each train delay cluster, train operation data of the case study intercity trains were extracted from the PIS called TTS-II during the pre-seasonal holiday on 15-23 December 2023, along with the other secondary data to be treated as predictors of delay propagation from the secondary data sources. The obtained data were cleansed and categorized into corresponding perspectives, including timetable, operation, and infrastructure perspectives. Then, the train delays were classified into clusters based on the k-mean cluster analysis and the elbow method. Then, for each delay cluster, level of train class, and type of track (i.e., double track, single track), multiple linear regression analyses were performed to investigate the influencing predictors of the delay propagation cluster. With the multi-objective optimization process, the optimal values of each predictor that yielded optimal solutions of delay propagation were derived subject to the defined objective and constraint functions. Consequently, the policy or measure to achieve each optimal predictor value with the corresponding investment cost (cost) as well as the delay savings were converted into a monetary benefit (benefit) using the value of time. Then, the benefit/cost (B/C) ratio of each scheme was evaluated. By ranking the B/C ratio, the policies or measures can be prioritized and incorporated into the masterplan for mitigating train delay propagation.
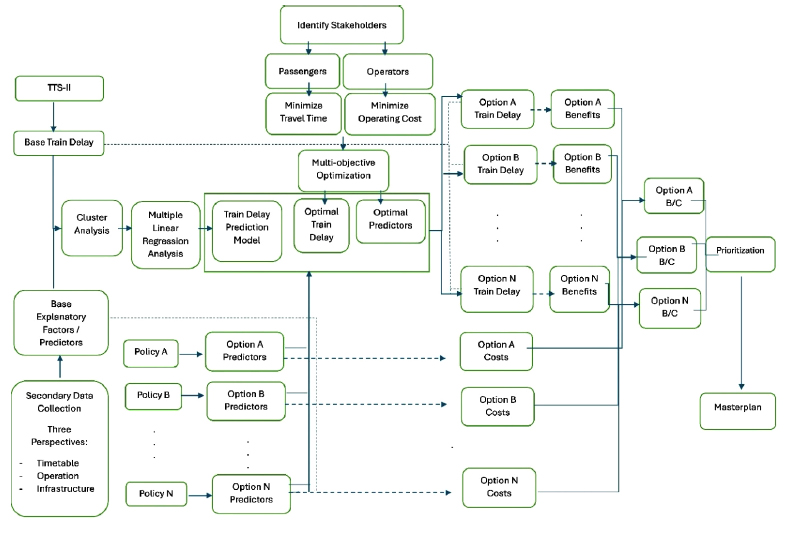
Model framework.
3.1. Research Framework
The framework of the research study involves the following steps:
1. Data collection from the Train Tracking System (TTS-II) and secondary sources
2. Data cleansing and categorization into timetable, operation, and infrastructure perspectives
3. Cluster analysis using k-means and the elbow method
4. Multiple linear regression analysis for each delay cluster, train class, and track type
5. Multi-objective optimization to derive optimal values for each predictor
6. Benefit-cost analysis of policy options
7. Prioritization of policies for incorporation into the masterplan for mitigating train delays
3.2. Input Data
3.2.1. Train Operation Data
The southern intercity railway route of Thailand usually experiences extensive delays in unpredictable patterns and, therefore, is considered a use case in this study. It comprises two sections, including an in-service double track system in the central section (from Bangkok Grand Terminal to Chumphon Junction, highlighted in blue) and the existing single track (with siding tracks), which continues further to the end of the line. (highlighted in yellow) as shown in Fig. (3). There are the list of intercity train operations includes the Special Express service (line numbers 31, 32, 37, 38, 39, 40, 43, 44, 45, 46), Express service (line numbers 83, 84, 85, 86), and Rapid service (line numbers 167, 168, 169, 170, 171, and 172) as summarized in A2 in the Appendix.
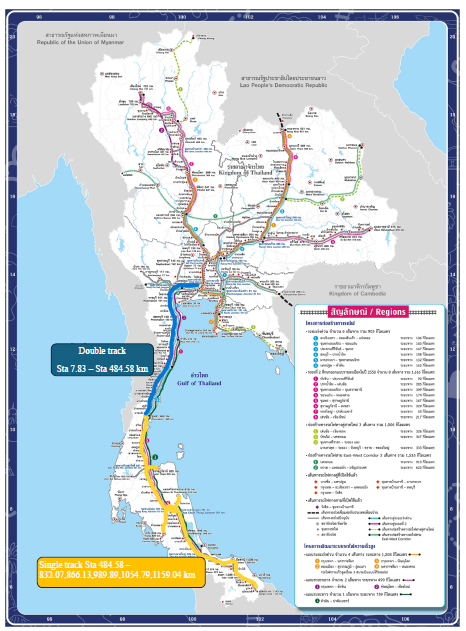
Map of SRT southern line (www.railway.co.th).
The State Railway of Thailand (SRT) provides a passenger information system (PIS) called the Train Tracking System (TTS-II), which runs on a daily, real-time basis. It indicates how much delays in train arrivals and departures deviate from the schedule. Fig. (4) illustrates the Train Tracking System (TTS-II), providing updated real-time information on the arrival and departure times of trains at each station. The list of intercity trains includes the Special Express service (line numbers 31, 32, 37, 38, 39, 40, 43, 44, 45, 46), Express service (line numbers 83, 84, 85, 86), and Rapid service (line numbers 167, 168, 169, 170, 171, and 172). The line numbers run on a directional pairwise basis. For example, 31 is an outbound train, and 32 is an inbound train or vice versa. For the current study, train operation data were collected on intercity trains for one week (15-23 December 2023).
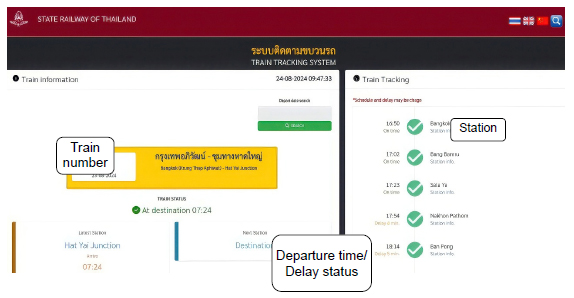
Screen display for TTS-II (www.railway.co.th).
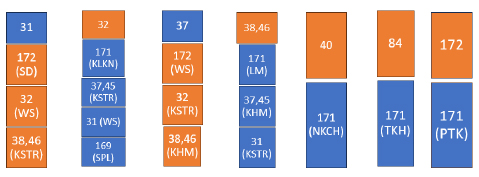
Train number with siding path.
Fig. (5) illustrates the examples of the dynamic nature of delay propagations that were identified on the single-track section of the Southern intercity railway route of Thailand. The blue box with an odd number means an outbound trip, while the orange box with an even number means an inbound trip, and an abbreviation stands for the station in which the trains are crossing each other.
3.2.1.1. Remarks
The letters appear in each box stand for station name including SD=Saeng Dad (km.484.58+4.01), WS=Wisai (km.484.58+12.38), KSTR=Khao Suan Tu Rian (km.484.58 +39.98), KLKN=Khlong Ka-Nan (km.484.58+72.5), SPL=Sa Phlee (km.469.85), KHM=Khuan Hin Mui (km.484.58+57.55), LM=La Mae (km.484.58+85.17), NKCH= Na Khon Chum (km.89.74), TKH= Tung KHA (km.484.58+12.38) and PTK=Pak Ta Ko (km.484.58 +48.28), respectively.
Train operation data were collected from the State Railway of Thailand's (SRT) passenger information system called the Train Tracking System (TTS-II) for one week (15-23 December 2023). The data includes information on Special Express, Express, and Rapid services operating on the Southern intercity railway route.
3.2.2. Influencing Factors Data
The factors or predictors under investigation, categorized into three perspectives (timetable, operation, and infrastructure factors), were collected at stations within every block section throughout the entire route. The timetable perspective focuses on planned/scheduled times when events are about to take place. The operation perspective considers the day-to-day control of the railway system, while the infrastructure perspective addresses the fixed assets used for the operation of the railway system. This paper considers only the timetable, operation, and infrastructure perspectives, as shown in Appendix A3, A4, and A5, respectively, while environmental, mechanical equipment, and human failure perspectives are not taken into consideration.
3.2.2.1. Model Assumptions
The following assumptions apply to model formulations.
1) The studied network and its various variables will not be disturbed by or disturb other railway systems.
2) Passengers' long-distance travel will be in a single manner, from the origin to the destination, with no transfers occurring.
3) For the southern route, SRT prioritizes outbound trains from Bangkok over inbound trains to Bangkok.
3.2.2.2. Model Notations
Model notations used in this paper are defined as shown in Table 1.
| Notations | Definition |
|---|---|
| Parameters | |
| L | Line length (unit: km) |
| R | Stopping cost per stop (unit: currency, THB) |
| h | Unit train running cost per unit length (unit: currency, THB/km) |
| Meff | Mass of each train type (unit: kg) |
| a | Acceleration (unit: m/s2) |
| p | Train horsepower (unit: hp) |
| δ | Average passenger travel time value (VTT) (unit: currency, THB/hour) |
| β | Coefficient of influencing factor |
| Variables | |
| G | Southern Intercity line, represented as G = (S, E) |
| S | Set of Intercity railway stations |
| Dt | Distances between stations i and j (unit: km) |
| m | Train stops mode, where m ∈ M = {mSE,mE,mR} |
| NS | Number of stops |
| nSE,nE,nR | Number of stops for each train type |
| CsVs | Stopping cost of all trains (unit: currency, THB) |
| CrVr | Running cost of all trains (unit: currency, THB) |
| Ce | Energy cost of all trains (unit: currency) |
| TD | Dwelling time at station s ∈ S (unit: minutes) |
| Vs | Scheduled running speed (unit: km/h) |
| Vr ∆x | Real running speed (unit: km/h) |
| Q | Total number of passengers |
| xmin,xmax | Minimum and maximum values of each influenced factor (units vary depending on the factor) |
| ∆x | Difference in value of each influenced factor (units vary depending on the factor) |
3.3. Objectives
The objective of this research is to lead to an understanding of the mechanisms of delay propagation and to provide insights into optimizing relevant variables to reduce delay propagation in transportation systems. The study will review articles supporting theories and optimization techniques to achieve this objective and improve the efficiency of transportation networks. The main objective of this research is to optimize the relevant variables to reduce delay propagation in various rail transit models. The specific objectives include:
1) Examine the relationships between variables associated with delay propagation. Conduct a comprehensive literature review on delay propagation and the optimization of related variables to understand the current state. Identify key factors influencing delay propagation and the impact of related variables on reducing delay propagation.
2) Explore current transportation mechanisms to obtain statistical values of various transportation variables. Analyse punctuality to enhance the optimization of relevant variable settings.
3) Identify variables significantly impacting the optimization of related variables, delay, and delay propagation models. Apply these to case study routes. Select representative case studies with different track forms, train schedules, and operational characteristics.
4) Evaluate models of policies related to reducing delay propagation. Assess their appropriateness for improving the reliability of travel times and the cumulative delay of the network throughout the journey using the relevant variables.
3.4. Methodology
3.4.1. Cluster Analysis
The k-means clustering technique was adopted to classify delay types. The optimal number of clusters was determined using the elbow method, resulting in four distinct delay clusters.
3.4.2. Multiple Linear Regression
For each delay cluster, train class, and track layout, multiple linear regression analysis was performed to identify the influencing predictors of delay propagation.
3.5. Objective Functions
SRT's long-distance trains must maintain their own benefits and profits while satisfying passengers' interests. From SRT's perspective, when developing a plan to minimize accumulated delays to improve passenger satisfaction, it is necessary to minimize various costs. This approach will attract more passengers to use long-distance trains. Therefore, appropriate policies should be arranged to address delay propagation in different clusters (Eqs. 3-6).
1) Minimize the operating cost of the intercity railway.
The cost of train stop C can be expressed as Eq. (1).
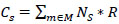 |
(3) |
The running cost of train C can be expressed as Eq. (2).
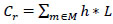 |
(4) |
The energy cost of train C can be expressed as Eq. (3).
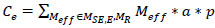 |
(5) |
2) Minimize train delay (the travel time of passengers)
The benefit of train delay of travel time passengers
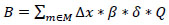 |
(6) |
3.7. Cost Calculation from Policy Options
The Calculation of the cost of each policy relies on how to achieve the optimal state of each influencing factor or predictor as shown in Table 2 (Eqs. 7-10).
3.8. Processing of Multi-objective
The model developed in this article is a Multi-Objective Programming Model (MOPM). Before solving the multi-objective model, a definite method must be used to convert the multi-objective model into a single model. The model has two goals in different dimensions, and the values in these different dimensions cannot be directly integrated. Furthermore, to address this issue, the concept of the Value of Travel Time (VOT) is introduced, which infers the price (baht/minute) to measure the value of passenger travel time. VOT is considered one of the most distinguished figures in transportation economics, and the assessment of VOT is widely supported by academic research and practical applications. Andrew Daly et al. (2019), in a study [16], pointed out that using VOT is crucial in evaluating transportation policies, such as infrastructure investment, which are affected by several factors.
| Policy | Concerned Factors | Goal |
|---|---|---|
| 1 | HeadwayBefore, HeadwayAfter | Adding new train units by comparing the cost-benefitof adjusting HeadwayBefore or HeadwayAfter time factors of each train class. |
| 2 | TotalDwell | Improving station platform layout by comparing the cost-benefit of adjusting TotalDwell time factor for passengers to make better alighting and boarding. |
| 3 | TotalSiding, Numberofsidingstation | Building a double track by comparing the cost-benefit of adjusting the TotalSiding time factor and the Numberofsidingstation factor. |
| 4 | RealSpeed, RunningtimeSupplements | Adjusting acceleration based on traction energy relies on tractive force based on two parameters, which is an effective mass (), train acceleration rate (a) and power (p) in equation consider specifically train acceleration towards RealSpeed and RunningtimeSupplements factors. |
| 5 | ScheduleSpeed | Adjusting service timetable by comparing the cost-benefit of adjusting the ScheduleSpeed factor to make a better service timetable. |
| 6 | NumberofStops | Adjusting the Number of stations by comparing the cost-benefit of adjusting the NumberofStops factor each train class. |
| 7 | Numberofjunction | Implementing a junction system by comparing the cost-benefit of adjusting the Numberofjunction factor for implementing a priority trains system. |
| 8 | level crossing | Upgrading level crossing by comparing the cost-benefit of adjusting the number of level crossings of each type that trains must proceed through, such as making Type3 into Type2 and building Type2 into Type1. |
| Parameter | Value |
|---|---|
| Train type | CDA5B1 for Special Express APD for Express, Rapid |
| Train cost | CDA5B1≈130 million baht APD≈14 million baht |
| VOT | 2.5 Baht/min/person |
| Stopping cost | 2,500 baht/station |
| Running cost | 300 baht/km |
| Double-track building cost | 24 million baht/168 km |
| Level crossing cost | Upgrading level 3 to level 2 ≈ 500,000 baht/point Upgrading level 2 to level 1 ≈ 50 million baht/point |
| Station platform layout cost | 1 million baht/station |
| Timetable service cost | 1 million baht/station |
| Frequency | 20 trains/day |
4. RESULTS AND DISCUSSION
4.1. Data
Main parameter table Southern line intercity railway, as shown in Table 3.
Table 3 outlines the critical operational parameters for the Southern Line, including train types, costs, frequency, and other key figures. These parameters form the baseline for modelling train operations and delay propagation. The differences in cost between Special Express and Express trains highlight the impact of operational efficiency on financial planning. The values, such as the excessive cost of constructing double tracks, emphasize the need for efficient delay mitigation strategies to justify infra- structure investments.
4.2. Cluster Analysis Results
The elbow method determined that k=4 was appropriate for the number of clusters of the dependent variable (DelayStation) from each factor perspective. The results are shown in the Appendix A6.
4.3. Multiple Linear Regression Results
The regression analysis revealed different influencing factors for each train class and track layout. For example, on double tracks, Special Express trains were significantly influenced by factors such as real speed, running time supplements, and the number of stops, as shown in A7-A9 in the Appendix. The table presents the results of the multiple linear regression analysis for clustered delays on double-track, single-track, Special Express, Express, and Rapid trains. The table categorizes delays into four clusters, indicating varying delay severity levels. The data illustrates the importance of variables such as real speed, running time supplements, and the number of stops. The model’s high R-squared values suggest that these factors strongly influence delay propagation, enabling operators to focus on specific areas for delay reduction, such as optimizing train speed and reducing the number of stops.
4.4. Optimal Point Between Influenced Factors in Clustered Delay
The analysis provided optimal values for each influencing factor across different delay clusters, train classes, and track layouts. These optimal values serve as targets for operational improvements. The values are shown in the Appendix. The tables compare the average and optimal values for key influencing factors across different delay clusters. The optimal values show where operational improvements can be made, such as increasing real speed or reducing the number of incidents. This optimization allows for a more targeted approach to delay mitigation, helping operators prioritize policies that will have the most significant impact on reducing delays across various clusters. For example, adjusting real speed and reducing the number of junctions can drastically improve travel times on double- and single-track layouts.
4.5. Evaluation of Benefits and Costs of Train Delay Mitigation Policy
The benefit-cost (B/C) ratio was used to evaluate the cost-effectiveness of different policy options. Policies with B/C > 1 were considered appropriate for implementation. as shown in Tables 4 and 5. For example, the cost of adjusting the acceleration policy in cluster 1 on double track in special express train class can be exemplified as 96 (train mass) * (∆xRealSpeed/∆xRunnitimeSupplement) * 2400 (horse power) and the benefit of delay travel time reduction is -0.088*(coefficient)* (∆xRealSpeed/∆xRunnitimeSupplement) *Number of passenger/year*VOT (baht/min/person).
The table compares different policy options for mitigating delays on double-track systems. Each policy option is associated with a cost and benefit (in million baht), which is evaluated using a benefit-cost (B/C) ratio. Policies such as adjusting train acceleration and reducing the number of stops are found to have high B/C ratios, particularly in early delay clusters. The cost-effectiveness of these policies demonstrates that early intervention in mitigating delays can yield substantial benefits, both in financial terms and operational efficiency.
| Track Layout | Train Class | Influenced Factor (Policy) | Benefit/Cost (million baht) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cluster1© | Cluster1(B) | Cluster2© | Cluster2(B) | Cluster3© | Cluster3(B) | Cluster4© | Cluster4(B) | B/C Ratio | |||
| Double track | Special Express | RealSpeed, RunningtimeSupplement (Adjusting acceleration) | 0.784 | 5.43 | 0.498 | 3.778 | 0.356 | 0.463 | 0.632 | 6.876 | 6.926/7.586/1.301/10.88 |
| Numberofstops (Adjusting number of stations) | 2.631 | 9.705 | 2.63 | 8.911 | 2.632 | 9.73 | 2.632 | 9.513 | 3.689/3.388/3.697/3.614 | ||
| NumberofIncidents | 526.825 | 7.315 | 630.93 | 19.268 | 601.71 | 21.956 | 81.54 | 5.27 | 0.014/0.031/0.036/0.065 | ||
| Type2samelevel | 526 | 5.678 | 630 | 17.422 | 599 | 16.578 | 80 | 2.214 | 0.011/0.028/0.028/0.028 | ||
| Type3unofficial (Upgrading level crossings) | 0.825 | 1.637 | 0.93 | 1.846 | 2.71 | 5.378 | 1.54 | 3.056 | 1.984/1.985/1.985/1.984 | ||
| Numberofjunction (Implementing junction system) | 3 | 3.896 | 3 | 4.831 | 6 | 8.735 | 8 | 10.919 | 1.298/1.61/1.456/1.365 | ||
| Double track | Express | Headwayafter (Adding new train unit) | 130 | 7.942 | 130 | 6.218 | 130 | 3.648 | 130 | 1.448 | 0.061/0.048/0.028/0.011 |
| Headwaybefore (Adding new train unit) | 130 | 9.492 | 130 | 6.746 | 130 | 1.403 | 130 | 4.907 | 0.073/0.052/0.011/0.038 | ||
| TotalDwell (Improving station platform layout) | 2 | 0.816 | 4 | 1.918 | 2 | 1.008 | 1 | 0.613 | 0.408/0.48/0.504/0.613 | ||
| ScheduleSpeed (Adjusting service timetable) | 8 | 3.484 | 20 | 8.24 | 18 | 7.418 | 14 | 5.78 | 0.436/0.412/0.412/0.413 | ||
| RealSpeed, RunningtimeSupplement (Adjusting acceleration) | 0.425 | 1.549 | 0.698 | 1.424 | 0.773 | 8.105 | 0.367 | 1.888 | 3.645/2.04/10.485/5.144 | ||
| Numberofstops (Adjusting number of stations) | 1.007 | 3.601 | 1.011 | 4.741 | 1.006 | 3.208 | 1.009 | 4.108 | 3.576/4.689/3.189/4.071 | ||
| Numberofjunction (Implementing junction system) | 3 | 11.949 | 3 | 16.389 | 2 | 9.903 | 2 | 8.45 | 3.983/5.463/4.952/4.225 | ||
| Double track | Rapid | Headwayafter (Adding new train unit) | 14 | 30.436 | 14 | 19.813 | 14 | 8.941 | 14 | 5.628 | 2.174/1.415/0.639/0.402 |
| Headwaybefore (Adding new train unit) | 14 | 3.183 | 14 | 3.718 | 14 | 2.411 | 14 | 2.044 | 0.227/0.266/0.172/0.146 | ||
| TotalDwell (Improving station platform layout) | 1 | 1.662 | 2 | 2.033 | 1 | 0.671 | 1 | 0.936 | 1.662/1.017/0.671/0.936 | ||
| ScheduleSpeed (Adjusting service timetable) | 14 | 5.987 | 9 | 3.785 | 7 | 2.965 | 7 | 3.214 | 0.428/0.421/0.424/0.459 | ||
| RealSpeed, RunningtimeSupplement (Adjusting acceleration) | 4.025 | 15.206 | 4.663 | 19.455 | 2.778 | 23.165 | 5.929 | 27.091 | 3.778/4.172/8.339/4.569 | ||
| Numberofstops (Adjusting number of stations) | 1.842 | 5.467 | 1.842 | 4.815 | 1.839 | 9.799 | 1.838 | 7.947 | 2.968/2.614/5.328/4.324 | ||
| Track Layout | Train Class | Influenced Factor (Policy) |
Costs/Benefits (million baht) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cluster1© | Cluster1(B) | Cluster2© | Cluster2(B) | Cluster3© | Cluster3(B) | Cluster4© | Cluster4(B) | B/C Ratio | |||
| Single track | Special Express | Headwayafter (Adding new train unit) | 130 | 0.577 | 130 | 0.404 | 130 | 0.343 | 130 | 0.445 | 0.004/0.003/0.003/0.003 |
| TotalSiding (Building double track) | 24 | 6.136 | 24 | 4.09 | 24 | 7.344 | 24 | 6.415 | 0.256/0.17/0.306/0.267 | ||
| Numberofsidingstation (Building double track) | 24 | 29.619 | 24 | 5.764 | 24 | 40.018 | 24 | 26.235 | 1.234/0.24/1.667/1.093 | ||
| ScheduleSpeed (Adjusting service timetable) | 4 | 1.535 | 1 | 0.119 | 3 | 1.102 | 22 | 7.558 | 0.384/0.119/0.367/0.344 | ||
| RealSpeed, RunningtimeSupplement (Adjusting acceleration) | 1.223 | 1.23 | 1.66 | 2.486 | 5.148 | 2.764 | 0.379 | 2.927 | 1.006/1.498/0.537/7.723 | ||
| Numberofstops (Adjusting number of stations) | 2.635 | 5.26 | 2.634 | 5.173 | 2.616 | 0.586 | 2.614 | 0.147 | 1.996/1.964/0.224/0.056 | ||
| Type2samelevel (Upgrading level crossings) | 28.5 | 0.152 | 229 | 1.223 | 293 | 1.562 | 193 | 1.028 | 0.005/0.005/0.005/0.005 | ||
| Type3unofficial (Upgrading level crossings) | 0.14 | 0.133 | 4.195 | 3.97 | 2.88 | 2.726 | 13.96 | 13.213 | 0.95/0.946/0.947/0.946 | ||
| Single track | Express | Headwayafter (Adding new train unit) | 130 | 0.313 | 130 | 2.161 | 130 | 2.174 | 130 | 1.282 | 0.002/0.017/0.017/0.01 |
| TotalDwell (Improving station platform layout) | 1 | 0.433 | 3 | 1.036 | 1 | 0.222 | 1 | 0.163 | 0.433/0.345/0.222/0.163 | ||
| ScheduleSpeed (Adjusting service timetable) | 9 | 4.047 | 7 | 3.062 | 7 | 3.378 | 9 | 4.201 | 0.45/0.437/0.483/0.467 | ||
| RealSpeed, RunningtimeSupplement (Adjusting acceleration) | 5.116 | 5.775 | 4.155 | 9.316 | 2.108 | 12.462 | 8.345 | 3.091 | 1.129/2.242/5.912/0.37 | ||
| Numberofstops (Adjusting number of stations) | 1.01 | 8.175 | 1.011 | 8.512 | 1.004 | 4.589 | 0.991 | 4.036 | 8.094/8.419/4.57/4.073 | ||
| NumberofIncidents (Upgrading level crossings) | 410.665 | 1.484 | 228.77 | 1.658 | 252.33 | 0.865 | 353.785 | 1.402 | 0.004/0.007/0.003/0.004 | ||
| Type2samelevel (Upgrading level crossings) | 410 | 1.087 | 227 | 0.602 | 252 | 0.668 | 353 | 0.934 | 0.003/0.003/0.003/0.003 | ||
| Type3unofficial (Upgrading level crossings) | 0.665 | 0.397 | 1.77 | 1.056 | 0.33 | 0.197 | 0.785 | 0.468 | 0.597/0.597/0.597/0.596 | ||
| Numberofjunction (Implementing junction system) | 2 | 3.433 | 2 | 4.246 | 3 | 6.548 | 3 | 5.036 | 1.717/2.123/2.183/1.679 | ||
| Single track | Rapid | Headwayafter (Adding new train unit) | 14 | 2.507 | 14 | 0.8 | 14 | 1.684 | 14 | 2.105 | 0.179/0.057/0.12/0.15 |
| Headwaybefore (Adding new train unit) | 14 | 2.507 | 14 | 0.8 | 14 | 1.684 | 14 | 2.105 | 0.179/0.057/0.12/0.15 | ||
| TotalSiding (Building double track) | 24 | 6.96 | 24 | 6.96 | 24 | 6.96 | 24 | 6.96 | 0.29/0.29/0.29/0.29 | ||
| Numberofsidingstation (Building double track) | 9 | 25.375 | 12 | 34.069 | 10 | 28.554 | 18 | 48.97 | 2.819/2.839/2.855/2.721 | ||
| RealSpeed, RunningtimeSupplement (Adjusting acceleration) | 0.567 | 2.684 | 1.018 | 2.371 | 0.986 | 3.404 | 0.872 | 3.737 | 4.734/2.329/3.452/4.286 | ||
| Numberofstops (Adjusting the number of | 1.834 | 1.047 | 1.835 | 1.564 | 1.836 | 2.27 | 1.837 | 3.5 | 0.571/0.852/1.236/1.905 | ||
| Numberofjunction (Implementing junction system) | 2 | 13.202 | 1 | 7.722 | 2 | 15.226 | 3 | 17.21 | 6.601/7.722/7.613/5.737 | ||
This table (Table 5) shows policy options similar to those in Table 4 but focuses on single-track systems. The cost of converting single-track sections to double-track is high, but the benefits in terms of delay reduction are equally significant. Policies such as upgrading level crossings and improving the number of siding stations are critical for minimizing delays on single tracks, where shunting and operational conflicts are more frequent. The table illustrates that infrastructure upgrades, while costly, can offer long-term solutions to recurring delays on single-track routes.
| Date | Train Number | Initial Delay Registration (mins) | Delay Registration (mins) | Station | Calculation (mins) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Passing | Waiting | Passing | Waiting | Passing | Waiting | Delayer train | Affected train | ||
| 15/12/23 | 31 | 172 | 5 | 26 | 71 | 55 | SD | 12 | 10 |
| - | 31 | 32 | 5 | 17 | 71 | 70 | WS | 15 | 19 |
| - | 31 | 38,46 | 5 | 10 | 71 | 88 | KSTR | 11 | 21 |
| - | 32 | 171 | 17 | 18 | 70 | 83 | KLKN | 10 | 21 |
| - | 32 | 37,45 | 17 | 22 | 70 | 52 | KSTR | 14 | 16 |
| - | 32 | 169 | 17 | 23 | 70 | 37 | SPL | 19 | 7 |
| - | 37 | 172 | 22 | 26 | 52 | 55 | WS | 10 | 10 |
| - | 37 | 38,46 | 22 | 10 | 52 | 88 | KHM | 9 | 18 |
| - | 38,46 | 171 | 10 | 18 | 88 | 83 | LM | 7 | 21 |
| - | 40 | 171 | 2 | 5 | 21 | 17 | NKCH | 1 | 5 |
| - | 84 | 171 | 28 | 18 | 62 | 83 | TKH | 16 | 14 |
| - | 171 | 172 | 28 | 26 | 62 | 55 | PTK | 14 | 16 |
4.6. Dynamic Delay Propagations
The study analyzed dynamic train delay propagations based on each train class and station, identifying delayer trains and affected trains. The propagation factor was calculated based on the provided equation (2), especially around Chum Phon station (end of double track) and an average buffer time between trains on a sample day (15/12/2023), as shown in Table 6.
Table 6 summarizes the dynamic delay propagation for different train numbers and stations. It highlights the interaction between trains in terms of delay propagation and recovery, using buffer times and station wait times. The analysis emphasizes how even minor delays can propagate across the network, particularly at key junctions. The findings reinforce the importance of optimizing operational schedules and prioritizing trains at critical stations to minimize cascading delays.
The mechanism of delay propagation occurring on a single track after Chumphon station in the upward direction (departing from Bangkok) and before reaching Chumphon station in the downward direction (arriving in Bangkok) can be explained based on the calculations according to equation (2). This happens when trains pass each other and must stop and wait at passing stations. The table shows which train passes and which train stops to wait, along with the delay from the previous station and the delay after leaving the passing station (delay data by station from TTS-II).
The calculation can be obtained from the delay of the previous train before arriving at the passing station, the number of blocks the train travels on a single track from the previous station to the passing station, and the buffer time of the two trains according to the train schedule. These variables yield the delay occurring on the single track. The various delays input into equation (2) are derived from data collected on TTS-II, and the appropriate delays are obtained from the cumulative delay model derived from multiple linear regression and multi-objective optimization.
4.7. Policy Recommendations
For double-track systems, train acceleration was adjusted, the number of stops was optimized, level crossings were upgraded, and priority systems were implemented at junctions.For single-track systems, policies similar to those in double-track systems were applied, with an additional focus on converting single tracks to double tracks.
4.7.1. Managerial Insights
This section serves to provide key takeaways and actionable strategies based on the results of the delay propagation and multi-objective optimization model without requiring an in-depth understanding of the mathematical complexities. The insights are framed to guide railway managers, planners, and decision-makers in implementing improvements that enhance service efficiency while minimizing operational costs.
4.7.2. Optimizing Train Schedules and Speeds
The results show that adjusting train acceleration and optimizing real-time speeds can significantly reduce cumulative delays. For instance, improving the running time supplements and real speeds between stations can help recover time lost during delays, especially for express and special express trains on double tracks. Managers should focus on real-time monitoring and dynamic adjustments to train speeds to keep schedules on track.
4.7.3. Reducing the Number of Stops
The analysis highlights that reducing the number of dwelling stations for certain trains, particularly on double-track systems, can have a substantial impact on reducing delays. For express and special express trains, the optimal number of stops was found to be significantly lower than the current average. This suggests that revisiting and adjusting station stop schedules, especially for high-priority trains, could streamline operations and enhance punctuality.
4.7.4. Infrastructure Upgrades at Key Junctions
One of the most impactful measures identified is improving junction systems to allow high-priority trains to pass without stopping. Furthermore, by prioritizing trains at key junctions, especially at stations with high traffic, overall network delays can be reduced. Investments in junction system upgrades can provide long-term benefits by minimizing bottlenecks that contribute to delay propagation.
4.7.5. Level Crossing Upgrades
Delays caused by unauthorized or congested level crossings are a significant factor. Upgrading lower-tier level crossings to higher tiers (e.g., converting Type 3 to Type 2 crossings) can greatly reduce incidents and delays on both single and double-track systems. This not only improves safety but also reduces train slowdowns, enhancing overall service efficiency.
4.7.6. Converting Single to Double Tracks
For sections of the network that are still single-track, the results support the conversion to double tracks as a means of reducing train shunting and delay propagation. This is particularly important for long-distance or high-speed trains, where waiting for other trains to pass can cause significant cumulative delays.
4.7.7. Cost-Effective Measures
The Benefit-Cost (B/C) ratio analysis in the study offers a clear guide for prioritizing investments. Policies such as reducing the number of stops and upgrading level crossings show a high B/C ratio, indicating that these measures are both effective and financially viable. Managers can use these insights to prioritize improve- ments that deliver the greatest returns in terms of delay mitigation [20-31].
CONCLUSION
From various literature reviews on cumulative delays occurring in rail systems, it has been found that the variables influencing cumulative delays in rail networks depend on the type of train and the type of track it is running on. Influential factors are divided into three categories: timetable perspective, operation perspective, and infrastructure perspective. To optimize double-track services for special express, express, and rapid trains, the key policies with high benefit-cost ratios (B/C>1) include adjusting train acceleration, reducing the number of stops, upgrading level crossings, and prioritizing systems at junctions. For special express trains, reducing number of stops to 14, upgrading type 3 crossings to type 2, and prioritizing junction systems significantly benefit delay clusters 1 (1-18 minutes) and 2 (19-47 minutes). For express trains, prioritizing junction systems, adjusting acceleration, reducing number of stops to 19, adding new train units, and adjusting timetables provide significant benefits for delay clusters 1 (1-21 minutes), 2 (22-45 minutes), 3 (46-69 minutes), and 4 (70-97 minutes). Rapid trains benefit from adjusting acceleration, reducing the number of stops to 41, adding new train units to reduce headway time to 18 minutes, and adjusting timetables, particularly for delay cluster 1 (1-21 minutes). Despite substantial costs, these measures enhance efficiency by minimizing delays, optimizing speeds, and reducing incidents.
For optimizing double-track services for special express trains, policies with a B/C>1 include changing the number of stops, building double tracks, and adjusting train acceleration. Upgrading level crossings and adjusting service timetables also significantly reduces delays, though costly. For express trains, the effective policies are changing the number of stops, prioritizing junction systems, and adjusting acceleration, while building double tracks is less effective due to operational patterns. Adjusting service timetables benefits all delay clusters. Rapid trains benefit from prioritizing junction systems, adjusting acceleration, and building double tracks. Despite the high implementation costs, these measures enhance efficiency by minimizing delays, optimizing speeds, and reducing incidents. The optimal number of stops and prioritized junction systems further reduce delays across all train types.
Prior to influencing variable investigation, the researchers categorized the types of delays using cluster analysis (elbow method) and identified four groups of delays. Subsequently, the variables influencing cumulative delays were examined using multiple linear regression analysis to determine the impact of each variable under different circumstances and to create a predictive model for cumulative train delays in various scenarios. Furthermore, using this model and the limitations of different variables, further analysis was conducted to find the optimal values for these variables compared to normal conditions using multi-objective optimization. This aimed to develop policies for improving train services in the Southern network using the B/C ratio method. Some policies were considered based on the B/C ratio, and some were considered based on the direct benefits of their policies.
The study found that, for double-track systems, the most appropriate policies include changing the acceleration rate of trains to increase their actual running speed, to compensate for delays, adjusting the number of stops, and improving the system at junctions before entering and after leaving stations. Without these improvements, delays would continue to accumulate progressively at stations. For single-track systems, similar policies are recommended, with an additional focus on converting single tracks to double tracks to reduce the need for trains to stop and wait for higher-priority trains. The more stations a train must stop and wait at, the more cumulative delays occur.
RECOMMENDATIONS FOR FUTURE RESEARCH
For future research related to the influencing factors, other variables could be considered, including rail system capacity or weather-related variables. Collecting data on these variables could be done in a stochastic manner that may lead to heuristic solutions for solving problems. This approach would support the analysis of a larger and faster dataset. When measuring the results, it might be useful to consider aspects such as capacity and multiple criteria decision analysis. The authors acknowledge and understand the limitations regarding the amount of data available for model creation. This is due to the small dataset, which is merely a protocol intended for further development in larger networks with more extensive data collection. Additionally, they recognize the constraints of the elbow method, which can lead to inaccuracies in selecting representative points for each group when building the model. These limitations may result in a model that is not entirely precise. For future work, the authors envision exploring alternative methods that could improve classification accuracy, aiming to identify true representatives of each group and thereby create a more precise model.
AUTHOR’S CONTRIBUTION
N.S.: Writing the Paper; Dr. A.S.: Study Concept or Design; Dr. W.S.: Research Advisor.
LIST OF ABBREVIATIONS
| HTM | = Historic train movements |
| INI | = Infrastructure information |
| OPI | = Operational information |
| EFW | = External factors and weather |
| MIP | = Mixed Integer Programming |
| VOT | = Value of Travel Time |
AVAILABILITY OF DATA AND MATERIALS
The data and supportive information are available within the article.
ACKNOWLEDGEMENTS
The authors would like to express their grateful appreciation to Kasetsart University for providing the scholarship that made this research possible and extend their gratitude to the State Railway of Thailand and the Department of Rail Transport for their generous data support.
APPENDIX
| Authors | Delay Propagation Model | Statistical Methods | Optimization | Solutions | Cost-effectiveness | |||
|---|---|---|---|---|---|---|---|---|
| Cluster Analysis | Multiple Linear Regression Analysis | Single Objective | Multi-objective | Exact | Heuristics | B/C | ||
| [1] | √ | x | x | x | x | x | √ | x |
| [2] | √ | x | x | x | x | x | √ | x |
| [3] | √ | x | x | x | x | x | √ | x |
| [4] | √ | x | x | x | x | x | √ | x |
| [5] | √ | x | x | x | x | √ | x | x |
| [6] | √ | x | √ | x | x | x | √ | x |
| [7] | √ | x | √ | x | x | x | √ | x |
| [8] | √ | √ | √ | x | x | x | √ | x |
| [9] | √ | x | x | x | x | x | √ | x |
| [10] | √ | x | x | √ | √ | √ | x | x |
| [11] | √ | √ | √ | √ | x | x | √ | x |
| [12] | √ | √ | √ | √ | √ | x | x | x |
| [13] | √ | x | x | x | x | x | x | x |
| [14] | √ | x | x | x | x | x | x | x |
| [15] | x | x | x | √ | √ | x | x | x |
| [16] | x | x | x | √ | √ | x | x | x |
| [17] | x | x | x | √ | √ | √ | x | x |
| [18] | x | √ | x | √ | √ | √ | x | x |
| [19] | x | √ | x | x | x | x | √ | x |
| [20] | √ | x | √ | x | x | √ | x | x |
| [21] | x | √ | x | x | x | x | x | x |
| [22] | x | x | √ | x | x | x | x | x |
| [23] | x | x | x | √ | √ | x | x | x |
| [24] | x | √ | x | x | x | x | x | x |
| [25] | x | x | √ | x | x | x | x | x |
| [26] | √ | x | x | x | x | √ | x | x |
| [27] | x | √ | x | x | x | x | x | x |
| [28] | √ | x | x | x | x | x | √ | x |
| [29] | √ | x | x | x | x | √ | x | x |
| [30] | x | x | √ | x | x | x | x | x |
| [31] | x | x | √ | x | x | x | x | x |
| [32] | x | √ | x | x | x | x | x | x |
| This paper | √ | √ | √ | √ | √ | √ | x | √ |
Table A2.
| Train Number | Train Type | Direction | Origin | Destination | Distance (km) |
|---|---|---|---|---|---|
| 31 | Special Express | Outbound | Bangkok (Krung Thep Aphiwat) | Hat Yai Junction | 945 |
| 32 | Special Express | Inbound | Hat Yai Junction | Bangkok (Krung Thep Aphiwat) | 945 |
| 37 | Special Express | Outbound | Bangkok (Krung Thep Aphiwat) | Su-Ngai Kolok | 1,147 |
| 38 | Special Express | Inbound | Su-Ngai Kolok | Bangkok (Krung Thep Aphiwat) | 1,147 |
| 39 | Special Express | Outbound | Bangkok (Krung Thep Aphiwat) | Surat Thani | 651 |
| 40 | Special Express | Inbound | Surat Thani | Bangkok (Krung Thep Aphiwat) | 651 |
| 43 | Special Express | Outbound | Bangkok (Krung Thep Aphiwat) | Surat Thani | 651 |
| 44 | Special Express | Inbound | Surat Thani | Bangkok (Krung Thep Aphiwat) | 651 |
| 45 | Special Express | Outbound | Bangkok (Krung Thep Aphiwat) | Padang Besar | 974 |
| 46 | Special Express | Inbound | Padang Besar | Bangkok (Krung Thep Aphiwat) | 974 |
| 83 | Express | Outbound | Bangkok (Krung Thep Aphiwat) | Trang | 828 |
| 84 | Express | Inbound | Trang | Bangkok (Krung Thep Aphiwat) | 828 |
| 85 | Express | Outbound | Bangkok (Krung Thep Aphiwat) | Nakhon Si Thammarat | 780 |
| 86 | Express | Inbound | Nakhon Si Thammarat | Bangkok (Krung Thep Aphiwat) | 780 |
| 167 | Rapid | Outbound | Bangkok (Krung Thep Aphiwat) | Kantang | 870 |
| 168 | Rapid | Inbound | Kantang | Bangkok (Krung Thep Aphiwat) | 870 |
| 169 | Rapid | Outbound | Bangkok (Krung Thep Aphiwat) | Yala | 1,026 |
| 170 | Rapid | Inbound | Yala | Bangkok (Krung Thep Aphiwat) | 1,026 |
| 171 | Rapid | Outbound | Bangkok (Krung Thep Aphiwat) | Su-Ngai Kolok | 1,147 |
| 172 | Rapid | Inbound | Su-Ngai Kolok | Bangkok (Krung Thep Aphiwat) | 1,147 |
| Factor | Description |
|---|---|
| Continuous variables | |
| HeadwayBefore | Time difference between the current and the preceding train within 5-580 minutes |
| HeadwayAfter | Time difference between the current and the succeeding train within 5-580 minutes |
| TotalDwell | Total time stopped at stations within 0-40 minutes |
| TotalSiding | Total times train stops and wait on siding track within 3-5 minutes |
| Binary variables | |
| DwellShort | Dwelling at station within 1-4 minutes (0,1) |
| DwellMedium | Dwelling at station within 5-9 minutes (0,1) |
| DwellLong | Dwelling at station within 10 minutes or more (0,1) |
| Sidings | Whether the train stops and waits on siding track (0,1) |
| Factor | Description |
|---|---|
| Continuous variables | |
| ScheduleSpeed | Train running speed between stations according to the schedule within 0-109.7 km/hr |
| RealSpeed | Train running speed between stations in real situation within 0-124.1 km/hr |
| RunningtimeSupplement | Running time that the train makes up for occurred delays, which is the difference between Schedule running time (distance between station/ScheduleSpeed) and real running time (distance between station/RealSpeed). Value range is within -78 to 33 |
| Numberofstops | Number of stations that the train stops at between origin to destination within 14-46 stations |
| NumberofIncidents (www.drt.gdcatalog.go.th) | Number of incidents that occur between stations and at a station since 2017 within 0-21incidents |
| Binary variables | |
| PriorityPattern1 | The priority train follows the rule “Special Express > the others (Express, Rapid)” (0,1) |
| PriorityPattern2 | The priority train follows the rule “Express > the others (Special Express, Rapid)” (0,1) |
| PriorityPattern3 | The priority train follows the rule “Rapid > the others (Special Express, Express)” (0,1) |
| Outbound | The train departs in an outbound direction (0,1) |
| Inbound | The train departs in an inbound direction (0,1) |
| Factor | Description |
|---|---|
| Continuous variables | |
| Distances (Dt) | Block section length between stations within 0-166.49 km. |
| NumberofJunction (Nj) | The number of junctions that trains cross through block section within 0-10 |
| Numberofsidingstation (NSD) | The number of siding stations that trains cross through block section within 0-4 |
| Numberoflevelcrossings* (Nlc) |
The number of level crossings along the block section between stations within 0-128 |
| Type1overpassunderpass (Nt1)* | The number of type1 level crossings that are overpass or underpass along the block section between stations within 0-28 |
| Type2samelevel (Nt2)* | The number of type2 level crossings that are level crossings along the block section between stations within 0-67 |
| Type3unofficial (Nt3)* | The number of type3 level crossings that are unofficial crossings along the block section between stations within 0-77 |
| Binary variables | |
| TracklayoutSingle (STl) | The train operates on Single track layout (0,1) |
| TracklayoutDouble (DTl) | The train operates on a double-track layout (0,1) |
| RouteConflictEntering (RCEj) | Junctions that the train must cross before entering station (0,1) |
| RouteConflictDeparting (RCDj) | Junctions that the train must cross before departing station (0,1) |
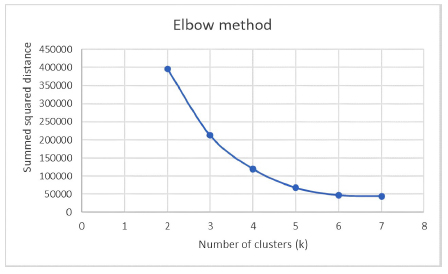
The elbow method results.
| Track Layout | Train Class | N | - | Adjust | Clustered Delay (mins); Average | B | β | t | Influenced Factor |
|---|---|---|---|---|---|---|---|---|---|
| Double track | Special Express | 762 | 0.850 | 0.847 | Cluster1 (1-18); 8.29 Cluster2 (19-47); 28.27 Cluster3 (49-76); 66.13 Cluster4 (77-113); 86 |
-.088 | -.061 | -1.968 | RealSpeed |
| -.847 | -.360 | -13.297 | RunningtimeSupplement | ||||||
| .974 | .130 | 7.216 | Numberofstops | ||||||
| .792 | .144 | 5.657 | Numberofincidents | ||||||
| 10.644 | .198 | 7.644 | Inbound | ||||||
| .239 | .237 | 5.681 | Distances | ||||||
| .390 | .165 | -4.967 | Type2samelevel | ||||||
| -.717 | -.140 | -5.506 | Type3unofficial | ||||||
| 10.521 | .767 | 24.773 | Numberofjunction | ||||||
| Double track | Express | 342 | 0.824 | 0.816 | Cluster1 (1-21); 8.58 Cluster2 (22-45); 34.25 Cluster3 (46-69); 57.38 Cluster4 (70-97); 80.95 |
.274 | .126 | 2.223 | HeadwayAfter |
| -.412 | -.226 | -3.234 | HeadwayBefore | ||||||
| .469 | .076 | 2.110 | TotalDwell | ||||||
| -.375 | -.182 | -3.072 | ScheduleSpeed | ||||||
| .264 | .160 | 2.399 | RealSpeed | ||||||
| -.797 | -.302 | -5.363 | RunningtimeSupplement | ||||||
| 29.774 | .522 | 5.762 | Inbound | ||||||
| 4.250 | .261 | 4.056 | NumberofJunction | ||||||
| Double track | Rapid | 764 | 0.723 | 0.715 | Cluster1 (1-22); 11.29 Cluster2 (23-43); 33.15 Cluster3 (44-65); 53.46 Cluster4 (66-105); 77.38 |
-.240 | -.319 | -4.791 | HeadwayAfter |
| -.052 | -.296 | -6.110 | HeadwayBefore | ||||||
| .593 | .093 | 3.403 | TotalDwell | ||||||
| .216 | .097 | 2.427 | ScheduleSpeed | ||||||
| -.207 | -.119 | -2.578 | RealSpeed | ||||||
| -.417 | -.129 | -3.039 | RunningtimeSupplement | ||||||
| -2.345 | -.157 | -2.698 | Numberofstops | ||||||
| 21.501 | .432 | 4.442 | Inbound | ||||||
| Single track | Special Express | 536 | 0.698 | 0.687 | Cluster1 (1-19); 6.85 Cluster2 (20-45); 31.97 Cluster3 (46-70); 59.38 Cluster4 (71-97); 81.54 |
-.008 | -.071 | -1.957 | HeadwayAfter |
| -6.718 | -.298 | -7.143 | TotalSiding | ||||||
| 24.647 | .616 | 9.105 | ScheduleSpeed | ||||||
| .250 | .200 | 3.367 | RealSpeed | ||||||
| -.204 | -.192 | -3.360 | RunningtimeSupplement | ||||||
| -.435 | -.254 | -6.223 | Numberofstops | ||||||
| -.460 | -.070 | -1.994 | Outbound | ||||||
| 21.825 | .462 | 7.090 | Distances | ||||||
| .207 | .301 | 3.950 | Numberofsidingstation | ||||||
| .193 | .096 | 1.544 | Type2samelevel | ||||||
| -.342 | -.224 | -2.957 | Type3unofficial | ||||||
| Single track | Express | 307 | 0.920 | 0.916 | Cluster1 (1-18); 7.11 Cluster2 (23-37); 30.85 Cluster3 (38-50); 44.06 Cluster4 (51-70); 56.64 |
-.073 | -.088 | -2.487 | HeadwayAfter |
| -.310 | -.054 | -2.150 | TotalDwell | ||||||
| -.418 | -.146 | -3.915 | ScheduleSpeed | ||||||
| .315 | .157 | 3.807 | RealSpeed | ||||||
| -1.537 | -.522 | -14.618 | RunningtimeSupplement | ||||||
| -1.398 | -.302 | -11.075 | Numberofstops | ||||||
| .468 | .078 | 2.079 | NumberofIncidents | ||||||
| 32.284 | .775 | 13.462 | Outbound | ||||||
| -.423 | -.067 | 2.113 | NumberofJunction | ||||||
| .120 | .045 | 1.616 | Type1overpassunderpass | ||||||
| -.270 | -.194 | -3.781 | Type2samelevel | ||||||
| 1.791 | .236 | 4.335 | Type3unofficial | ||||||
| Single track | Rapid | 1207 | 0.802 | 0.798 | Cluster1 (1-20); 10.83 Cluster2 (21-42); 29.52 Cluster3 (43-67); 54.83 Cluster4 (68-99); 79.26 |
.063 | .062 | 3.710 | Headwayafter |
| .018 | .063 | 3.308 | Headwaybefore | ||||||
| 1.718 | .053 | 1.442 | TotalSiding | ||||||
| -.089 | -.055 | -1.908 | RealSpeed | ||||||
| -.373 | -.077 | -3.186 | RunningtimeSupplement | ||||||
| -1.461 | -.093 | -4.613 | Numberofstops | ||||||
| .142 | .091 | 4.013 | Outbound | ||||||
| 6.769 | .303 | 14.715 | Distances | ||||||
| 3.186 | .390 | 13.229 | Numberofsidingstation | ||||||
| 35.477 | .685 | 23.772 | NumberofJunction |
Table A8.
| Track Layout | Train Class | Influenced Factor | Average Case | Optimal Value | |||||
|---|---|---|---|---|---|---|---|---|---|
| Minimize | Cluster1 | Cluster2 | Cluster3 | Cluster4 | maximize | ||||
| Double track | Special Express | RealSpeed | 70 | 63 | 68 | 65 | 61 | 63 | 59 |
| RunningtimeSupplement | -3 | -1 | -4 | -5 | -6 | -7 | -8 | ||
| Numberofstops | 21 | 14 | 14 | 14 | 14 | 16 | 20 | ||
| NumberofIncidents | 6 | 1 | 1 | 1 | 2 | 1 | 1 | ||
| inbound | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Distances | 40 | 21 | 37 | 18 | 23 | 32 | 16 | ||
| Numberofjunction | 5 | 1 | 1 | 1 | 1 | 4 | 4 | ||
| Type2samelevel | 14 | 2 | 2 | 3 | 7 | 13 | 13 | ||
| Type3unofficial | 3 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| Double track | Express | Headwayafter | 47 | 24 | 24 | 28 | 31 | 40 | 39 |
| Headwaybefore | 46 | 40 | 39 | 41 | 36 | 41 | 41 | ||
| TotalDwell | 4 | 1 | 1 | 1 | 2 | 4 | 4 | ||
| ScheduleSpeed | 65 | 65 | 60 | 50 | 43 | 47 | 45 | ||
| RealSpeed | 61 | 59 | 52 | 46 | 46 | 46 | 48 | ||
| RunningtimeSupplement | -3 | -6 | -15 | -16 | -11 | -18 | -13 | ||
| Numberofstops | 23 | 18 | 20 | 19 | 18 | 18 | 20 | ||
| inbound | 0 | 0 | 0 | 0 | 1 | 1 | 1 | ||
| Numberofjunction | 5 | 1 | 1 | 1 | 4 | 5 | 5 | ||
| Double track | Rapid | Headwayafter | 55 | 16 | 18 | 18 | 18 | 18 | 18 |
| Headwaybefore | 107 | 23 | 23 | 28 | 28 | 33 | 33 | ||
| TotalDwell | 3 | 2 | 1 | 1 | 3 | 2 | 2 | ||
| ScheduleSpeed | 67 | 52 | 53 | 59 | 60 | 60 | 60 | ||
| RealSpeed | 63 | 59 | 54 | 54 | 54 | 44 | 44 | ||
| RunningtimeSupplement | -2 | -14 | -16 | -18 | -24 | -24 | -24 | ||
| Numberofstops | 43 | 41 | 41 | 41 | 41 | 41 | 41 | ||
| inbound | 0 | 0 | 0 | 1 | 1 | 1 | 1 | ||
| Track Layout | Train Class | Influenced Factor | Average Case | Optimal Value | |||||
|---|---|---|---|---|---|---|---|---|---|
| Minimize | Cluster1 | Cluster2 | Cluster3 | Cluster4 | maximize | ||||
| Single track | Special Express | Headwayafter | 111 | 50 | 60 | 59 | 59 | 63 | 89 |
| TotalSiding | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| numberofsidingstation | 1 | 1 | 1 | 1 | 2 | 2 | 2 | ||
| ScheduleSpeed | 67 | 69 | 62 | 60 | 67 | 67 | 79 | ||
| RealSpeed | 65 | 66 | 67 | 63 | 72 | 65 | 72 | ||
| RunningtimeSupplement | -3 | -2 | -2 | -3 | -4 | -6 | -6 | ||
| Numberofstops | 22 | 14 | 14 | 14 | 21 | 22 | 22 | ||
| outbound | 0 | 0 | 0 | 0 | 1 | 0 | 0 | ||
| Distances | 45 | 13 | 13 | 13 | 47 | 61 | 61 | ||
| Type2samelevel | 12 | 10 | 10 | 10 | 11 | 13 | 13 | ||
| Type3unofficial | 16 | 13 | 13 | 13 | 15 | 15 | 15 | ||
| Single track | Express | Headwayafter | 38 | 21 | 21 | 21 | 21 | 38 | 38 |
| TotalDwell | 2 | 1 | 1 | 1 | 1 | 2 | 2 | ||
| ScheduleSpeed | 67 | 72 | 73 | 75 | 75 | 79 | 79 | ||
| RealSpeed | 63 | 56 | 48 | 48 | 48 | 57 | 57 | ||
| RunningtimeSupplement | -2 | -1 | -3 | -5 | -5 | -5 | -5 | ||
| Numberofstops | 24 | 18 | 18 | 20 | 23 | 24 | 24 | ||
| Single track | Express | NumberofIncidents | 3 | 6 | 8 | 11 | 12 | 18 | 18 |
| outbound | 1 | 0 | 0 | 0 | 1 | 0 | 0 | ||
| Type1overpassunderpass | 4 | 1 | 1 | 1 | 1 | 3 | 3 | ||
| Type2samelevel | 12 | 3 | 3 | 6 | 6 | 8 | 8 | ||
| Type3unofficial | 14 | 10 | 10 | 11 | 13 | 18 | 18 | ||
| Numberofjunction | 5 | 4 | 4 | 4 | 4 | 5 | 5 | ||
| Single track | Rapid | Headwayafter | 24 | 22 | 30 | 30 | 33 | 33 | 33 |
| Headwaybefore | 47 | 26 | 28 | 28 | 38 | 38 | 38 | ||
| TotalSiding | 5 | 4 | 4 | 4 | 5 | 5 | 5 | ||
| RealSpeed | 62 | 66 | 69 | 68 | 74 | 74 | 74 | ||
| RunningtimeSupplement | -2 | -3 | -3 | -3 | -4 | -4 | -4 | ||
| Numberofstops | 43 | 42 | 42 | 42 | 43 | 43 | 43 | ||
| outbound | 0 | 0 | 1 | 1 | 0 | 0 | 0 | ||
| Distances | 21 | 21 | 21 | 25 | 28 | 28 | 28 | ||
| Numberofsidingstation | 5 | 2 | 2 | 3 | 3 | 4 | 4 | ||
| Numberofjunction | 5 | 4 | 4 | 5 | 5 | 5 | 5 | ||