All published articles of this journal are available on ScienceDirect.
Short Review in Green Vehicle Routing Problem with Pick-up and Delivery and Time Windows Using Metaheuristics
Abstract
Integrating sustainability is a crucial process that every organization must incorporate into its supply chain. Transportation is one of the primary contributors to carbon emissions, accounting for approximately 24% of global CO2 emissions. Notably, road transport is responsible for nearly 75% of these total emissions worldwide, according to recent studies conducted by the International Energy Agency (IEA) in 2021.
This paper explores the Green Vehicle Routing Problem (GVRP), which represents an extension of the classical Vehicle Routing Problem (VRP). GVRP integrates environmental considerations by focusing on reducing the carbon footprint. Within this framework, we focus on the Green Vehicle Routing Problem Pickup and Delivery with Time Windows (GVRPPDTW) variant, which introduces additional complexity by requiring vehicles to serve customers with specific pickup and delivery requests within predefined time windows. This variant reflects realistic constraints in the logistics field, such as schedule synchronization and the balance between efficiency and customer satisfaction. This study presents a short comprehensive review conducted over the period 2017-2024, identifying and analyzing research conducted in the context of this variant and analyzing the efficiency of using metaheuristic algorithms in solving this optimization problem. We will discuss existing research gaps and propose future directions for further advancements in the field. This analysis aims to provide a comprehensive understanding of GVRPPDTW, offering valuable insights for researchers and practitioners seeking to address its challenges.
1. INTRODUCTION
The distribution industry and transportation fulfill an essential role in the global economy by smoothing the flow of goods and services between countries and regions. However, the industry also contributes significantly to carbon emissions, a major cause of climate change. Transportation contributes over 24% of the world's CO2 emissions from fuel burning, with road transportation alone accounting for almost three-quarters of these emissions [1]. These emissions have a significant negative influence on the environment, contributing to air pollution, global warming, and harmful health impacts.
The VRP is considered an NP-hard combinatorial optimization problem [2]. It involves determining the optimal paths for several vehicles to deliver things to a group of clients, minimizing total distance or cost while adhering to various constraints. Over the years, VRPs have evolved to encompass numerous variants, each addressing specific logistical challenges.
The Pickup and Delivery with Time Windows (PDTW) is a significant variation of the VRP, which involves vehicles handling both pick-ups and deliveries within the same route. This variant requires vehicles to respect precedence constraints, meaning each item must be picked up before it is delivered while also respecting time windows. Additionally, the vehicles have the capacity constraints that need to be taken into account [3]. The PDTW involves managing a series of customer needs that must be satisfied by a series of vehicles, each with various constraints to consider. Typically, the trajectory of a vehicle begins and finishes at a central depot. Requests have to be collected at specific locations and delivered to the appropriate destinations. Pick-ups must take place before deliveries, and the same vehicle must handle both pick-up and delivery pairs. PDPTW is particularly relevant in industries such as ride-sharing, courier services, and reverse logistics, where efficient management of both PD operations is essential.
To satisfy a series of needs, the Vehicle Routing Problem Pickup and Delivery with Time Windows (VRPPDTW) mostly entails transportation tasks. However, these transportation activities negatively impact the environment through pollution and CO2 emissions.
This paper presents a structured literature review that focuses on research conducted on the GVRPPDTW, which adds the “Green” aspect to this optimization problem. The primary objective is to examine the various methods used in association with GVRPPDTW and explore related studies to identify potential avenues for future research.
The organization of the paper will be as follows: Section 2 will provide a literature review for the GVRPPDTW approach. Section 3 will address the mathematical modeling, and Section 4 will discuss the metaheuristics approaches for GVRPPDTW. Section 5 will delve into the various research gaps identified for GVRPPDTW. Finally, we will conclude with a summary and suggestions for future work.
2. LITERATURE REVIEW
The literature review conducted in this study follows a structured approach to ensure a comprehensive understanding of the GVRPPDTW and the applications of metaheuristic algorithms. We selected and analyzed all relevant papers within this scope from the following databases: SCOPUS, Web of Science, and Google Scholar. Our review focused on studies that explored GVRPPDTW using metaheuristic approaches published between 2017 and 2024. Notably, we did not find any papers addressing this variant using these methods before 2017.
2.1. Vehicle Routing Problem and its Variants
The Vehicle Routing Problem (VRP) was first introduced in 1959 [2]; this problem is considered as an important NP-hard combinatorial optimization problem in logistics and operational research. The main goal of classical VRP is to find the optimal routes for a fleet of vehicles that must start and end at a central depot to serve a set of customers to minimize operational costs. Since VRP is NP-hard, the computational feasibility of solutions is complex with increasing problem size; in practice, heuristics and metaheuristics are applied to serve this complexity and provide optimal solutions.
The literature on VRP research is growing, and this article will purposefully and quickly examine some of it. It established the truck dispatching problem, proposing a paradigm in which a single operations center supplies a fleet of uniform vehicles with the gas needed by several locations [2]. The goal of this concept was to reduce the truck drivers' distances between the stations.
Later, this subject was expanded [4] into a linear optimization issue, which typically addressed logistics and transportation operations incorporating a group of clients, depots, and a collection of vehicles. One of the earliest works closely resembles modern VRP models [4]. Subsequently, researchers in this domain have explored techniques and frameworks to enhance the routing issue and provide superior solutions. Models of routing problems were proposed [5], taking into account varying speeds and being time-dependent. Incorporating time-based features into VRP models was a significant milestone.
The VRP has been extensively studied by researchers. An overview of earlier research up to 1992 on classic VRP models, including exact algorithms and heuristic algorithms [6].
Research [7] examined the generic version of the TSP issue, known as the multiple traveling salesman problem (mTSP). The current VRP was developed as a consequence of this dilemma, which allows several salespeople to sell goods in a distribution chain. Reducing transportation costs was, nevertheless, a primary focus of VRP issues until recently.
The following flowchart represents the variants of the VRP:
Fig. (1) provides a complete categorization of the VRP and its extension, including the GVRP, highlighting their structural variations. It organizes the problem into specific configurations based on parameters such as the number of routes (single or multiple), vehicles (single or multiple), depots (single or multiple), fleet type (homogeneous or heterogeneous), vehicle capacity (limited or unlimited), delivery type (single or pick-up and delivery) and the presence of time constraints (with or without time windows). GVRP emphasizes sustainability by focusing on minimizing environmental impacts, such as CO2 emissions, making it a central model for environmentally friendly logistics. This classification framework facilitates solution approaches for various logistics scenarios, particularly in the field of sustainable transport.
In this paper, we study the combination of the GVRP extension with the two variants Pickup and Delivery, and the time windows, which represent our GVRPPDTW variant.
2.2. Green Vehicle Routing Problem Pickup and Delivery with Time Windows
The GVRP is a concept introduced in 2012 as an alternative that takes into consideration the environmental damage caused by greenhouse gas emissions; this work demonstrated the feasibility of optimizing routes while accounting for environmental constraints, providing the foundation for future research in green logistics [8].
Additionally, a suggested heuristic technique produced an acceptable degree of accuracy when solving VRP, including PD. As was previously indicated, there are significant savings when commodities are picked up and delivered via common routes; however, this has not been well studied [9].
Researchers have recently shown a great deal of interest in GVRP because of its possible economic and environmental advantages. The goal of GVRP is to lower vehicle carbon dioxide emissions using a variety of techniques. For example, a study [10] conducted research that examined ways to lower carbon dioxide emissions. They proposed a model that balanced the conflicting objectives of maintaining financial profits and lowering pollution by using a capacitated vehicle routing issue and a multi-objective optimization approach. Furthermore, an environmental viewpoint on capacity constrained VRP with time windows. The model was based on a reasonable distribution arrangement and included variable speed restrictions for different times of the day [10, 11].
The Pick-Up and Delivery Problem (PDP) is a VRP variant considered a logistics and optimization challenge commonly encountered in transportation, supply chain management, and distribution networks. It involves designing efficient routes for vehicles to fulfill a set of transportation requests, where each request requires an item to be picked up at one location and delivered to another. Fig. (2) below represents a scheme of a network of PDP transportation.
The GVRPPDTW aims to minimize costs by efficiently allocating vehicles and routes, taking into account PD, vehicle load, time specifications, and ecological constraints. GVRPPDTW is focused on distributing and collecting items within a time-constrained transportation network. The PD system describes how the vehicle meets the demand at the destination node. The time windows reflect the specific periods when the fleet arrives at the customer's node. Each truck is required to adhere to two sorts of time windows to deliver items to clients within a specific period. The environmental impact represents the CO2 emission reduction. The vehicle might not arrive at the client's location before opening time or after closing. The optimum path should be timely, fulfill capacity needs, and reduce distance and cost [12].
In Table 1 below, we present the works that have dealt with GVRPPDTW using metaheuristic approaches, focusing on the objective function studied, the metaheuristic method used, and the typology of the algorithm (H: Hybrid, S: Single).
Based on the above table, we observe that the GVRPPDTW is a highly relevant and contemporary research topic. The majority of the studies have been conducted within the past five years, highlighting the growing interest in this field and providing an opportunity to identify research gaps that can be addressed in future work. Additionally, we note that most studies have utilized the Genetic Algorithm, reflecting its adaptability for large-scale problems and its flexibility across various domains. In the following sections, we will present a comparative analysis of the most commonly used algorithms in these studies and discuss the results they have achieved.
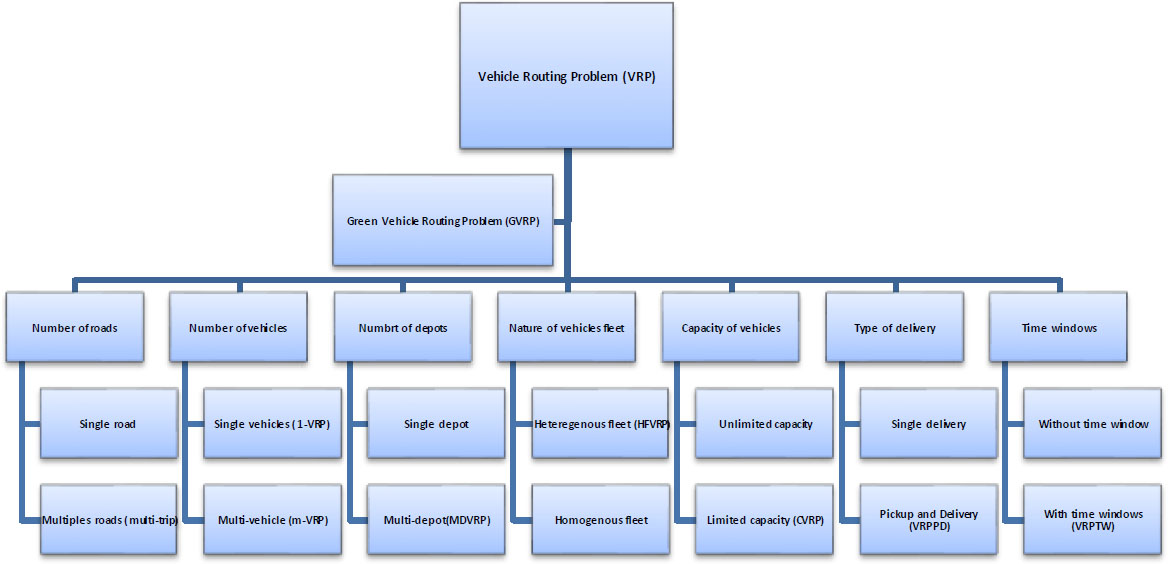
Representation of the variants VRP.
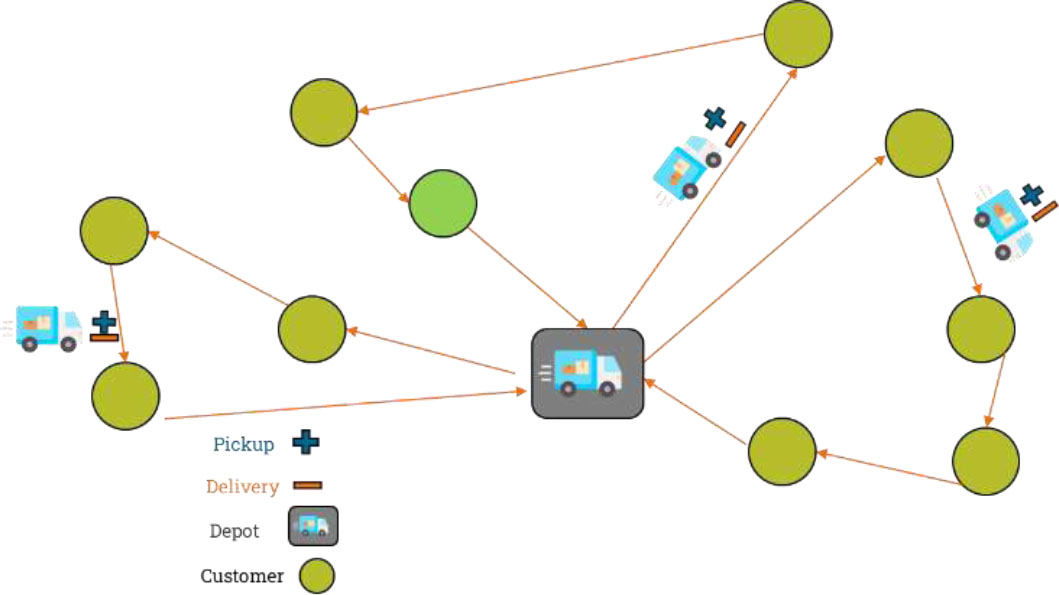
Pickup and delivery transportation network.
| Year | Objective Function | Metaheuristic Approach | H/S | References |
|---|---|---|---|---|
| 2017 | Minimize total distribution costs including transportation, refrigeration, damage, and carbon emission costs | Cycle Evolutionary Genetic Algorithm (CEGA) | S | [13] |
| 2019 | Minimize fixed costs, transportation costs, refrigeration costs, cargo damage costs, and carbon emissions in cold chain logistics | Genetic Algorithm (GA) | S | [14] |
| 2019 | Minimize total costs, including carbon emissions, fixed vehicle costs, transportation costs, and penalty costs | Adaptive Genetic Hill-Climbing Algorithm (AGHCA) | H | [15] |
| 2020 | Minimize CO2 emissions and delivery costs | Genetic Algorithm (GA) + Local Search (LS) | H | [16] |
| 2020 | Minimize fuel consumption and CO2 emissions in pickup and delivery with time windows | Hybrid Discrete Artificial Bee Colony (HDABC) | H | [17] |
| 2021 | Minimize distribution cost and CO2 emissions | Simulated Annealing Algorithm (SAA) + Local Search (LS) | H | [12] |
| 2021 | Minimize total costs, including fuel and carbon emission costs, while satisfying customer demands within specified time windows. | A genetic algorithm is proposed, utilizing different crossover (one-point, two-point, cyclic) and mutation (swap, inverse) operators | S | [18] |
| 2022 | Achieve low-carbon vehicle routing | Tabu Search (TS) + Genetic Algorithm (GA) | H | [19] |
| 2022 | Minimize costs associated with transportation, refrigeration, and emissions and consider service time windows | Genetic Algorithm (GA) | S | [14] |
| 2024 | Minimize energy consumption by optimizing both delivery routes and speeds, adhering to time window constraints. | Genetic Algorithm (GA) | S | [20] |
3. MATHEMTICAL FORMULATION
3.1. Problem Definition
We have based our research on various studies of the GVRPPDTW. It is important to note that most potential constraints have been proposed in the past two decades, especially when sustainability is considered one of the most challenging aspects that should be integrated into the optimization of this type of logistics problem.
GVRPPDTW problem is a significant logistics issue in many applications, including beverage distribution, container transport, and so on. In today's competitive market, companies are increasingly focused on reducing total costs. The supply chain network consists of n nodes (customers and suppliers) and a single depot. The optimization model involves assigning the different nodes to different routes, minimizing the total distance traveled. The goal is to minimize the overall cost of transportation while fulfilling all consumer requests. This expense is correlated with the quantity of vehicles utilized and the distance traveled by every vehicle while respecting each customer's time window.
3.2. Mathematical Model
Let a graph be G = (N, A).
N = {i ∈ N/i = 0,1, 2,…,n} is the node-set, where n indicates a location.
The depot is indicated by node 0.
We have a pair of PD sites for each request. Let;
N+ = {i ∈ N / i =1, 2,…, n/2}: pick-up locations
N- = {i ∈ N / i = (n/ 2) + 1,…, n} delivery locations.
In GPDPTW, the objective is to design a set of routes in such a way that:
(1) Only one vehicle at a time may satisfy a node (supply or customer);
(2) There is just a single depot;
(3) Constraints on capacity must be maintained;
(4) There are strict constraints for arrival times;
(5) Every vehicle leaves the depot at the beginning of its journey and should return to the depot at the end.
While the request is processed, the vehicle stays stopped at a node.
A vehicle should wait if it arrives at node i before the start of its period (ai).
GVRPPDTW is expressed mathematically as a combination of a few studies [21, 22] and [11].
The following parameters describe the problem:
N: A list of the depot, supplier, and customer nodes;
N': List of nodes for suppliers and customers;
N+: list of the nodes that provide;
N-: Each customer node;
K: Number of vehicles;
dij: The distance between nodes i and j; if dij = ∞, there is no path between i and j (dead end, pedestrian street,...);
tijk: The amount of time it takes for vehicle k to get from node i to node j;
(ai, bi): The time window for each node i;
sti: Time stopping at node i;
qi: Quantity to be processed at node i
If qi > 0, the node is a supplier;
If qi < 0, the node is a customer;
If qi = 0 then the node has been served.
Wk: Capacity of vehicle k,
i = 0..N: Index of predecessor nodes,
j = 0..N: Index of successor nodes,
k = 1..K: vehicle index,
Xijk: 1 If vehicle k travels from node i to node j else 0
Ai: Arrival time at node i,
yik: Amount in vehicle k that is at node i;
Ck: The vehicle k's transportation cost.
Our objective function is to minimize the total cost of each vehicle from i to j:
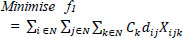 |
The environmental aspect of the GVRPPDTW is quantified through CO2 emissions, which are calculated based on fuel consumption influenced by various transport-related factors. Here is a formulation for the GPDPTW that incorporates the time window, total tour duration, vehicle capacity, service time, and fuel consumption rate to minimize CO2 emissions. The formula for fuel consumption, detailed [22], depends on the vehicle's load and the distance driven.
To calculate the rate of fuel consumption, we used the formula below:
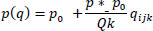 |
Such as:
∂: the CO2 emission factor according to the type of fuel
p: full load fuel consumption rate
p0: initial fuel consumption rate with an empty load
q: distance traveled on arc ij
qijk: the load of vehicle k when it traverses arc (i,j)
Wk: The total capacity of vehicle k
So our second objective function will formulated as:
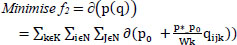 |
Now, we can deduct the total objective function: (Eq. 1)
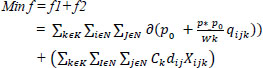 |
(1) |
Subject to:
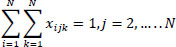 |
(2) |
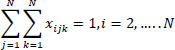 |
(3) |
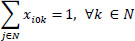 |
(4) |
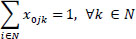 |
(5) |
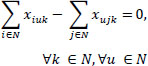 |
(6) |
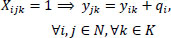 |
(7) |
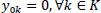 |
(8) |
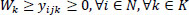 |
(9) |
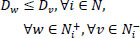 |
(10) |
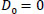 |
(11) |
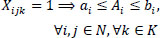 |
(12) |
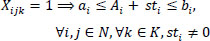 |
(13) |
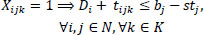 |
(14) |
Eqs. (2 and 3) confirm that a single vehicle serves each node. Eqs. (4 and 5) ensure that a vehicle's availability is not exceeded, meaning that a car only ever departs and returns to the depot. The node visited must likewise be departed from, according to Eq. (6), which guarantees the continuation of a vehicle tour. It is ensured by Eqs. (7-9) that a vehicle's transport capacity is not exceeded. Eqs. (10 and 11) ensure that precedence constraints are respected. Finally, Eqs. (12-14) verify that time windows are respected.
4. METAHEURISTICS ALGORITHMS APPLIED FOR GVRPPDTW
Similar to VRP, GVRP is a combinatorial optimization problem that is NP-hard. Generally, the solution techniques suggested in the literature provide solutions through the use of exact or approximate algorithms. Exact algorithms are typically employed for small instances, especially when the problem's domain is narrow and manageable. In the broader and more complex domain of the problem, approximate algorithms are the most suitable methods for obtaining near-optimal solutions. For further information about both exact and approximate algorithms, we suggest consulting [23].
In this section, we will discuss different metaheuristics, which are a class of approximate algorithms designed to solve complex optimization problems. Unlike exact algorithms, which guarantee finding an optimal solution within an acceptable computing time limit, metaheuristics seek to identify a decent, frequently close to ideal solution. This balance between solution quality and computational efficiency makes metaheuristics particularly suitable for solving large-scale, complex problems where exact methods become impractical.
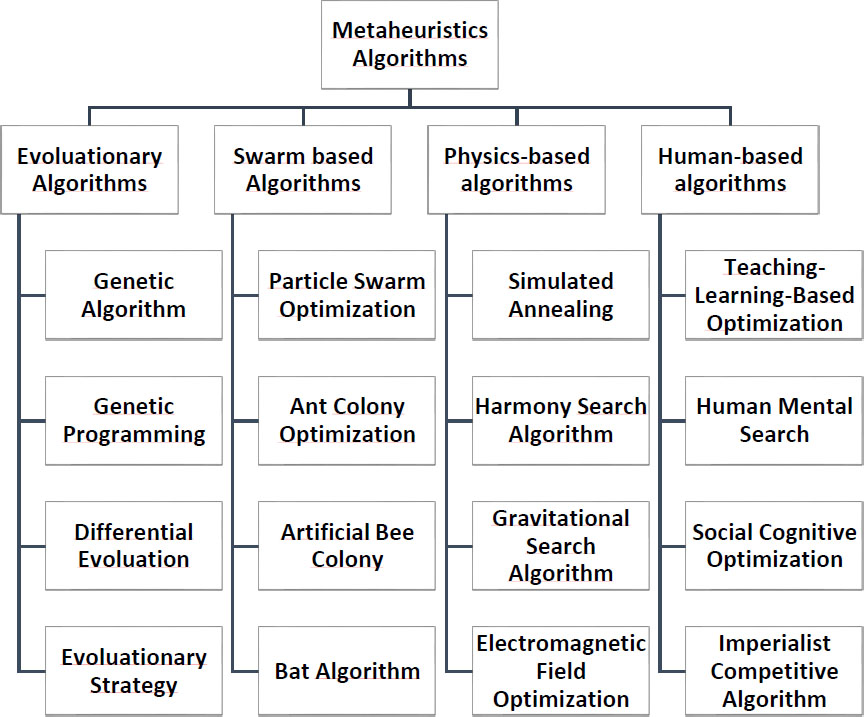
Fig. (3) below shows a classification of types of metaheuristics that can be used to solve the GVRPPDTW based on a literature review.
4.1. Evolutionary Algorithms
This category of algorithms is inspired by the behavior of Darwin’s theory of evolution. Each iteration in such an algorithm is known as a generation and is composed of parent selection, recombination (crossover), mutation, and survivor selection. While crossover and mutation are responsible for the exploration, parent, and child selection brings out the exploitation. One of the most popular evolutionary algorithms is the Genetic Algorithm (GA), first introduced in 1975 [24], by researchers who had developed an optimization method that mimicked the process of natural evolution. Each solution in a population was assigned a fitness value, and the algorithm iteratively bred new populations to search for optimal or near-optimal solutions. In 1989, a study [25] extended the first work in GA to reach the application of this algorithm in engineering problems. By the year 1992, the concept of GA had been developed into Genetic Programming (GP), where the evolved solutions were not fixed-length chromosomes but programs or functions represented as trees [26]. Later, in 2002, x the researchers proposed the NSGA-II (Non-dominated Sorting Genetic Algorithm II), one of the most efficient and widely used algorithms for multi-objective optimization [26, 27].
4.2. Swarm Intelligence-based Algorithms
This second category of metaheuristics algorithms, known as swarm intelligence, is inspired by the way social animals communicate and share knowledge within a group during the optimization process. These swarm algorithms (SA) are modeled on the collective behavior of animals and insects, such as ants and bees. The core idea behind these algorithms is that the information exchanged among individuals in the swarm directly influences each agent’s movement and decisions. By managing the flow of information between agents, swarm algorithms achieve a balance between exploration and exploitation. The first formal introduction of swarm intelligence as a concept was in 1989 [28]. The Ant Colony Algorithm was first introduced [29], inspired by the foraging behavior of real ants, which deposit pheromones to mark good paths to food sources. Artificial ants mimic this process, with pheromone trails guiding their search for optimal solutions. Later, in 2005, the Artificial Bee Colony was developed [30]; this algorithm has been widely applied to optimization problems, such as scheduling, function optimization, and clustering.
4.3. Physics-based Algorithms
The third category of metaheuristic algorithms consists of physics-based techniques, which replicate natural physical principles to guide the optimization process toward the best solution. These techniques are inspired by the fundamental laws of physics. One of the most widely used algorithms in this category is Simulated Annealing (SA), modeled after the metallurgical process of annealing, where materials are heated and then slowly cooled to minimize energy and reach a stable, optimized structure. The first time introduced the Simulated Annealing Algorithm was in 1983 by [31], who applied it to the
Classification of metaheuristics.
Traveling Salesman Problem (TSP) and demonstrated that the algorithm could escape local optima and converge to global solutions.
4.4. Human-based Algorithms
This category of algorithms is related to techniques inspired by human social behavior, decision-making processes, and problem-solving strategies. One of the most notable human-based algorithms is the Teaching-Learning-Based Optimization (TLBO), introduced in 2011 [32]. TLBO models the relationship between a teacher, which is considered “the best solution,” and students, considered “individual solutions,” allowing individuals to improve by learning phases.
In what follows, we have conducted a comprehensive comparison of four prominent metaheuristics—Genetic Algorithm (GA), Simulated Annealing (SA), Tabu Search (TS), and Local Search (LS)—that are widely employed for addressing GVRPPDTW. Table 1 shows that these are the algorithms most frequently used in works already dealing with GVRPPDTW.
Based on our literature review, each metaheuristic offers distinct advantages and limitations in optimizing complex routing scenarios while considering environmental factors and logistical constraints. GA excels in exploring large solution spaces but may suffer from slow convergence, whereas SA's probabilistic approach aids in escaping local optima but requires careful parameter tuning. TS provides robust solutions by intensively searching the solution space but may struggle with computational complexity, while LS efficiently improves solutions through iterative local improvements but may be sensitive to initial conditions. By evaluating these metaheuristics comprehensively, we aim to provide insights into their applicability and effectiveness in enhancing the sustainability and efficiency of vehicle routing operations under green logistics initiatives.
We have provided more details in Table 2 below.
| Method | Description | References |
|---|---|---|
| Genetic algorithm (GA) |
Genetic algorithms mimic natural selection processes, employing crossover, mutation, and selection to iteratively improve solutions across generations. They excel in global exploration due to the diverse initial populations they generate. They are highly adaptable to diverse constraints and specific objectives of the PDPTW. Genetic algorithms can swiftly converge to acceptable solutions early on, but they are prone to premature convergence, potentially getting stuck in local minima if population diversity decreases. For large-scale problems, especially with sizable populations and numerous generations, computation times can become lengthy. | [33-35] |
| Tabu search (TS) | Tabu search utilizes adaptive memory to prevent cycles and encourage the exploration of novel solutions by maintaining a “tabu” list of previously explored solutions. This approach facilitates intensified exploration, effectively navigating away from local minima. It offers flexibility in incorporating specific constraints, such as time windows, which enhances its applicability to complex problem instances. Tabu search performs well for structured problems where incremental improvements in solution quality are achievable through neighbor moves. However, its implementation can be complex, particularly in managing the tabu list effectively. Additionally, the quality of the final solution is often influenced by the initial solution chosen, highlighting its dependence on the starting point. | [36, 37] |
| Simulated annealing (SA) | Simulated annealing emulates the gradual cooling process of metals, enabling movement towards lower-quality solutions initially to avoid local minima, with this probability decreasing over time. It excels in escaping local minima by temporarily accepting less optimal solutions. The algorithm is straightforward to implement and modify, offering parametric flexibility where temperature and cooling parameters can be adjusted to enhance performance. However, its effectiveness is highly sensitive to these parameters, influencing its ability to converge to an optimal solution. Simulated annealing can exhibit slow convergence, particularly for large-scale problems, necessitating careful parameter tuning for optimal results. | [37, 38] |
| Local search (LS) | Local search is valued for its simplicity in implementation, making it straightforward and efficient to program. It adapts readily to various constraints specific to the PDP with Time Windows (PDPTW), such as time windows and vehicle capacities. Its flexibility allows integration into hybrid approaches, enhancing overall algorithm efficiency; for instance, it can complement more complex methods like tabu search or genetic algorithms to refine solutions. However, local search is prone to converging towards local minima, limiting its ability to explore and find globally optimal solutions. Moreover, its performance heavily relies on the quality of the initial solution; starting with a suboptimal solution can hinder its effectiveness. Furthermore, local search only explores the immediate neighborhood, constraining its exploration capability compared to more exploratory metaheuristics. | [39, 40] |
| Algorithm | Key Findings | References |
|---|---|---|
|
Genetic algorithm (GA) |
The GA quickly and effectively seeks optimal solutions for GVRPPDTW. By combining inversion mutation and insertion mutation operators, the results show that both carbon emission costs and total distribution costs increase with the rise of carbon tax between the values of 0 to 90. The analysis of cost proportions reveals that carbon emission costs can constitute a significant portion of 67% of total distribution costs, particularly at higher carbon tax levels. | [13] |
| The application of GA has reduced the traveled distances and fuel consumption, so directly lowering carbon emissions. It facilitates simultaneous pickup and delivery, enhancing vehicle capacity utilization and decreasing the number of trips required. | [14] | |
| A comparative study demonstrates that the application GA in the context of reducing the carbon footprint helped to minimize more than 5 kg of CO2 emissions. The study addressed by this paper identifies an effective carbon tax interval, within which increasing the carbon tax leads to reduced carbon emissions. | [15] | |
| The GA effectively manages various constraints, such as time windows and vehicle capacities, ensuring that logistics operations are both efficient and aligned with sustainability goals. The GA successfully identifies optimal delivery routes that minimize travel distances, which is crucial for reducing fuel consumption and carbon emissions. |
[14] | |
| Simulated Annealing (SA) | The algorithm generated an effective vehicle route plan that minimized costs and emissions. The results indicated a 15-20% reduction in transportation costs |
[12] |
| Local Search (LS) | The integration of LS as a hybridization with GA has provided results that were closely aligned with those obtained from exact methods, but it did so in a significantly shorter time frame, making it suitable for large-scale problems | [16] |
| Tabu Search (TS) | The application of TS with GA exhibits better global convergence ability and robustness compared to other algorithms like the genetic algorithm (GA) and particle swarm optimization (PSO). While GA has good solution effects, it suffers from longer calculation times and slower convergence. In contrast, the GA-TS algorithm achieves faster convergence and maintains strong solution performance even with a large number of customers. It has shown significant reductions in total costs associated with vehicle scheduling. Specifically, it can reduce costs by 31.1% compared to other methods and by 60.03% when compared to the particle swarm optimization algorithm. This demonstrates the algorithm's effectiveness in optimizing not just travel time but also fuel consumption and carbon emissions | [19] |
We will present in the following Table 3 the results of these four algorithms as applied to the context of the GVRPPDTW, based on our analysis of previous studies. This discussion will provide insights into their performance, strengths, and limitations, highlighting how each algorithm contributes to addressing the complexities of the GVRPPDTW.
5. DISCUSSION
Based on the analysis of algorithms and results applied to the GVRPPDTW, several research gaps have emerged. First, while many studies focus on reducing CO2 emissions, few explore the dynamic integration of real-time data, such as traffic conditions and demand fluctuations, which are critical for practical implementation. Second, most studies utilize single or hybrid metaheuristic algorithms, yet there is limited research comparing these with emerging approaches like deep reinforcement learning or machine learning-enhanced metaheuristics. Furthermore, the trade-offs between minimizing CO2 emissions and operational costs, particularly in scenarios with variable carbon tax policies, remain underexplored. Another significant gap lies in the scalability of these solutions, as most algorithms are tested on mid-sized problem instances, leaving their performance on large-scale, real-world datasets uncertain. Lastly, while some studies incorporate specific application contexts such as cold chain logistics or urban distribution, a more holistic approach to multi-sectoral applications could provide broader insights. Addressing these gaps will enhance the practicality and robustness of GVRPPDTW solutions in achieving both environmental and operational efficiency [3, 19, 41-49].
CONCLUSION
To conclude, there has been an increasing focus on green logistics. Within this framework, GVRP and its variants have garnered significant attention from researchers throughout the previous twenty years. With an emphasis on GVRPPDTW and associated studies, we presented a comprehensive review for the GVRPPDTW research in the literature. In addition, a review of the VRP and GVRPPDTW is established and the methods for finding solutions were examined. The GVRPPDTW problem is resolved using exact or approximative methods such as metaheuristics. We have presented a summary of the most used algorithms in solving GVRPPDTW.
As a future direction, we propose to maintain a study that includes electric and hybrid vehicles for further CO2 reduction in the context of GVRPPDTW. In addition, integrating Machine Learning can enhance metaheuristic algorithms by improving adaptability and efficiency. Furthermore, we propose to address future models that consider carbon pricing and environmental regulations, with more real-world case studies needed to validate these approaches in practice.
AUTHORS’ CONTRIBUTIONS
It is hereby acknowledged that all authors have accepted responsibility for the manuscript's content and consented to its submission. They have meticulously reviewed all results and unanimously approved the final version of the manuscript.
LIST OF ABBREVIATIONS
| IEA | = International Energy Agency |
| GVRP | = Green Vehicle Routing Problem |
| GVRPPDTW | = Green Vehicle Routing Problem Pickup and Delivery with Time Windows |
| PDTW | = Pickup and Delivery with Time Windows |
| VRPPDTW | = Vehicle Routing Problem Pickup and Delivery with Time Windows |
| PDP | = Pick-up and Delivery Problem |
| SA | = Swarm Algorithms |
| SA | = Simulated Annealing |
| TLBO | = Teaching-Learning-Based Optimization |
| GA | = Genetic Algorithm |
| TS | = Tabu Search |
| LS | = Local Search |
ACKNOWLEDGEMENTS
Declared none.


