All published articles of this journal are available on ScienceDirect.
A Study of Smart Grid Effects on Electric Vehicle Management Considering the Change of the Power Capacity Mix
Abstract
Background:
To understand the Electric Vehicle (EV) management effects deeply using Smart Grids (SGs) in the electric power sector, it is necessary to examine supply specifics such as the generation mix, generation costs, and CO2 emissions as well as the demand sector including peak load. This study attempts to comprehensively examine the changes in power supply and demand their effects in accordance with the degree of SG utilization, based on a scenario for the projection of EV roll-out in South Korea.
Objectives:
This study considers the change of the generation capacity mix as well as the change of power generation mix using the WASP model for the analysis of SG effects on EV management. In the scenario of the Korean government's EV deployment, this study has confirmed how electric power demand changes according to the degree of smart grid utilization. In addition, the WASP model has been used to examine not only the power generation mix but also the change in the installed capacity.
Result:
As a result, if the share of cost-effective and clean power generation sources is below the minimum load, the unit cost and CO2 emission could not be reduced together even though SGs are used to manage EVs.
Conclusion:
Increasing the share of power generation from clean energy sources to a level higher than that of the minimum load will allow EVs to become an eco-friendly means of transportation.
1. INTRODUCTION
The use of Electric Vehicles (EVs) as eco-friendly alternatives recently has been increasing, and they are becoming one of the significant factors in the long-term increase of electric power demand. According to the International Transport Forum (ITF) [1], the electricity demand of EVs will exceed 20% of global demand in the most optimistic scenario where EVs will have replaced all fossil-fuel based vehicles in the world by 2050. European Environment Agency (EEA) [2] forecasted that the demand share of electric cars to total electricity demand would reach levels of 4-5% in several European countries by 2030 and makeup 9.5% by 2050 with an electric car stock penetration of 80% according to the EV-high scenario.
Although EVs do not have a severe impact on the power grid in the short-term, they will occupy an increasingly higher proportion of the electric power load with long-term diffusion. Moreover, as EV charging becomes concentrated during specific time-slots or at the peak of the energy demand, the power supply may also become unstable.
Smart grid (SG) technologies provide a function for transferring the charging load from a peak to an off-peak time-slot. Thus, the daily load curve is steadied, helping to reduce the investment in power plants and electrical networks. Also, EVs can function as decentralized storage equipment by using SG technologies. This vehicle-to-grid (V2G) technology transfers the electricity from EV batteries to the grid when there is a power overload, thereby stabilizing the power grid [3-7].
Many studies have been conducted on the impact of EVs on the electricity demand and the effects of smart charging and demand response. Some studies such as Darabi and Ferdowsi [8], Weiller [9], Shao et al. [10], Bahrami and Parniani [11], Mohammadi and Rabinia [12], García-Álvarez et al. [13], Gnann et al. [14] and Lyon et al. [15] analyzed the impact of EVs on the electricity demand profile and emphasized the importance of smart charging and demand response. Amini et al. [16] analyzed the simultaneous allocation of EVs’ parking lots and distributed renewable resources in smart power distribution networks. These studies did not, however, deal with V2G. Meanwhile, Kempton and Tomić [17] developed an equation for calculating the energy that EVs provide to the grid through V2G. The IEA [18] analyzed the degree to which SGs could reduce the expected increase in peak load as a result of EV charging and the effectiveness of V2G in different countries. Choi et al. [19] analyzed the peak load management effect of V2G as a function of the degree of SG utilization, based on the projections of EV dissemination in South Korea. Lopez et al. [20] reviewed demand-side management in SG operation considering EV load shifting and V2G. These studies mainly focused on the means by which increases in peak load, caused by the diffusion of EVs, can be mitigated by smart charging and V2G support.
However, in order to comprehensively understand the EV management effects using SGs in the electric power sector, it is necessary to examine supply specifics (such as the generation mix, generation costs, and carbon dioxide (CO2) emissions) as well as the demand sector (including peak load) [21, 22]. Some studies analyzed the impacts of EV on generation costs and CO2. Weis et al. [23] reviewed the potential of controlled EV charging to reduce operational and capacity expansion costs for electric power systems. Sorrentino et al. [24], Lucas et al. [25], Doucette and McCulloch [26], Delgado et al. [27], Choma and Ugaya [28] and Croziera, et al. [29] assessed the potential impact of EVs on CO2 according to different generation mixes. Zhang et al. [30] carried out an economic and environmental analysis of EVs with different operational conditions. These studies contributed to helping us understand the impacts of EVs on generation costs and CO2 emissions. Nevertheless, they had limitations on the analysis of the impacts of EVs on the electricity demand sector and reviewed EVs’ impacts at a given installed capacity mix, without considering the change of the capacity mix.
This study attempts to comprehensively examine the changes in power supply and demand and their effects in accordance with the degree of SG utilization, based on a scenario for the projection of EV roll-out in South Korea. The SG utilization is focused on coordinating charging and discharging of EVs. This work may contribute to studies related to the interaction among EVs, SGs, and electricity systems in terms of technical, economic, and environmental aspects. The projection of EV deployment in South Korea is based on the study by Choi et al. [14], which was carried out in the Korean Energy Economics Institute as a national research project. The model of Wien Automatic System Planning Version 4 (WASP-IV) and the results of the 2nd Korean Energy Master Plan (2014~2035) and the 7th Basic Plan for Long-term Electricity Supply and Demand (2015-2029) are used in analyzing the impacts of EVs and SGs (Fig. 1).
The structure of this study is as follows. In Chapter 2, it sets the SG utilization cases and analyzes the impact of EVs on peak load and the effects of the SGs. Chapter 3, it examines the power generation mix and power capacity mix by case and analyzes the influence of EV management of the SGs on power generation cost and CO2 emission. Chapter 4 discusses the analysis results, and Chapter 5 presents conclusions.
2. THE IMPACT OF EVS ON PEAK LOAD AND THE EFFECTS OF THE SG
2.1. Charging Capacities of EVs
The charging capacity depends on the specifications of the charging devices. The specifications of charging devices can be classified with relatively simple speculations. The USA Department of Energy groups charging devices into 1.44, 3.3 and 60-150 kW. The categories used by EDF, the French Electricity Provider, are 3, 6, 24, 43, and 150 kW. The larger the capacity of the charger, the faster it can charge [31].

The advantage of rapid charging is the short time period required for complete charging. However, it is not generally used because of the associated high cost and potential shortening of the battery life-span. Rheinisch-Westfӓlische Technische Hochschule Aachen (RWTH) [32] forecasted that 90% of EVs would be charged by slow charging and the remaining 10% by fast charging. Based on this projection, the IEA [18] has assumed that the average charging capacity would be 7.3 kW, given that the slow charging capacity is 3.7 kW and the fast charging capacity is 40 kW [18, 32]. This study has implemented these assumptions.
2.2. Discharging Capacities of EVs
EVs transfer the surplus electricity to the power grid through discharging. Kempton and Tomić [12] defined the EV energy transfer to the power network using equation (1).
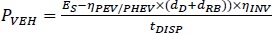 |
(1) |
where PVEH (kW) is the maximum electric power transferable through V2G, ES (kWh) is the battery-stored energy available as direct current transferable to an inverter, dD (km) is the driving distance when the battery of an EV is fully charged, dRB (km) is the minimum range buffer driving distance required for a driver, ηPEV/PHEV (kWh/km) is the average driving efficiency of pure EVs (PEVs) and plug-in EVs (PHEVs), ηINV is the efficiency of the inverter where the direct current of the battery converts into alternating current, and, finally, tDISP (hour) is the time that the stored energy in EVs is dispatched.
In accordance with the IEA [18] and SNE Research [33], ES is assumed to be 30 kWh for PEVs and 10.7 kWh for PHEVs. ηPEV/PHEV is assumed to be 0.15 kWh/km through a review of Korean cases. dD is influenced by various features such as driving behavior, vehicle type, and the charging schedule of drivers. In South Korea, the average daily driving distance is 28 km per driver.
dRB is not an engineering figure that can be calculated through a study of car features. dRB is determined by the driver or the car operating company. The buffer driving distance is reserved for unexpected journeys to locations such as convenience stores or hospitals. Through interviews with drivers in California, USA, Kurani et al. [34] suggested that 32 km, which is around 63% of the average daily driving distance per person in the USA, was the range buffer recognized by most drivers. Based on these findings, the range buffer driving distance in this study was set as 20 km, which is 70% of the average daily driving distance per driver in South Korea. As PHEVs can be operated with their internal combustion engine even when they are discharged entirely, dRB of a PHEV was set as zero. ηINV was set as 0.93, conforming to the assumptions made by Kempton and Tomić [17].
tDISP can range between a few minutes for spinning reserve and a few hours for peak load response. According to the IEA [18], peak load occurs for three to five hours per day. As this study examines the effects of EVs on peak load, tDISP was set as three to four hours. The forecasted number of disseminated PEVs and PHEVs are similar in agreement with the IEA [35]. Therefore, PVEH (kW) operates as an average of the PEVs and PHEVs. Given the assumptions above, the discharging capacity was calculated to be about 4 kW.
2.3. The Controlling Effect of SGs on the EV Impact on Peak Load
The proportion of EVs that are connected to the power grid during peak load greatly affects the overall impact of EVs on the load of the electric power network. The IEA [18] has assumed that the proportion of EVs connected to the power grid during peak hours, without SG utilization, is 50%. Korea Power Exchange (KPX) [36] assumed the proportion is 30% and Choi et al. [19] assumed 40%. This study considers all precedent studies on the electric vehicle charging share during peak hours.
The SGs can lessen the load by partially disconnecting EVs from the power grid or lowering the charging capacity during peak load. The EV charging management market is expected to grow with the already matured technologies. As V2G is cost intensive and demands additional infrastructure to enable bilateral power flow between EVs and the power grid, however, it is forecasted to grow at a slower rate than the EV charging management market. The battery of an EV participating in V2G experiences functional degradation earlier than that of a non-participating EV. The costs of the functional degradation of the batteries must be incorporated into the compensation offered to the consumer by the power provider. However, it is not easy to quantify functional degradation into a monetary value. Furthermore, as a consumer participates in V2G, the shortened driving distance necessitates frequent charging, thereby resulting in lower acceptance of V2G over the grid to vehicle (G2V).
Table 1 provides three types of SG utilization in parallel with the IEA [18]. Without SG utilization (labeled SG Non-Utilization), the proportion of G2V during peak load time is 30% or 40% or 50% with no V2G. The two other types, in accordance with dynamic pricing and the degree of SG utilization, are divided into SG Low-Utilization and SG High-Utilization.
Table 1 shows that a total of 9 analysis cases have been drawn based on the degree of SG utilization and the charging and discharging share during the peak hours; fEV (G2V) is decreased by 10%p, fEV (V2G) is increased by 5%p as the degree of SG utilization rises. The following is an overview of the cases.
| Category | fEV(G2V)(%) | fEV(V2G)(%) | fEV(G2V)(%) | fEV(V2G)(%) | fEV(G2V)(%) | fEV(V2G)(%) |
|---|---|---|---|---|---|---|
| SG Non-Utilization | Case 1 | Case 4 | Case 7 | |||
| 30 | 0 | 40 | 0 | 50 | 0 | |
| SG Low-Utilization | Case 2 | Case 5 | Case 8 | |||
| 20 | 5 | 30 | 5 | 40 | 5 | |
| SG High-Utilization | Case 3 | Case 6 | Case 9 | |||
| 10 | 10 | 20 | 10 | 30 | 10 | |
- Case 1: fEV (G2V) is 30%. There is no SG utilization.
- Case 2: fEV (G2V) is 10%p less than Case 1 and fEV (V2G) is 5%p more than Case 1.
- Case 3: fEV (G2V) is 20%p less than Case 1 and fEV (V2G) is 10%p more than Case 1.
- Case 4: fEV (G2V) is 40%. There is no SG utilization.
- Case 5: fEV (G2V) is 10%p less than Case 4 and fEV (V2G) is 5%p more than Case 4.
- Case 6: fEV (G2V) is 20%p less than Case 4 and fEV (V2G) is 10%p more than Case 4.
- Case 7: fEV (G2V) is 50%. There is no SG utilization.
- Case 8: fEV (G2V) is 10%p less than Case 7 and fEV (V2G) is 5%p more than Case 7.
- Case 9: fEV (G2V) is 20%p less than Case 7 and fEV (V2G) is 10%p more than Case 7.
The effect of EVs on the peak load can be expressed as equation (2) [18]. The coefficient δ is determined by multiplying the proportion of EVs charging during peak load time by the average charging electric power (7.3 kW) of each EV. The coefficient ε is determined by multiplying the proportion of EVs discharging during peak load time by the average discharging electric power (4 kW) of each EV. NPEV/PHEV is the number of EVs at time (t). Taking advanced metering infrastructure (AMI) into account is important because V2G is available after the environment is prepared where demand response is possible through AMI.
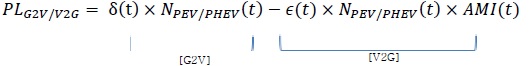 |
(2) |
There is a time-lag between the establishment of AMI and the functioning of V2G. V2G must first be commercialized with V2G-supported AMI being deployed in advance. South Korea plans to distribute smart meters to every household by 2020 and optimize the demand response system for reasonable energy consumption through additional updates of the metering system by 2030. It may be assumed that AMI deployment would be complete by 2030. However, the effect of AMI on V2G will differ according to the timing of V2G commercialization and the degree of V2G-supported AMI dissemination. This study has assumed that the V2G-supported AMI roll-out will begin in 2020 and be completed in 2035, with V2G being available as soon as V2G-supported AMI is established.
It is assumed that the V2G-supported AMI deployment will show exponential growth in the early stage, gradually slowing down and finally maturing when AMI is distributed to almost all households. The proportion of the V2G-supported AMI roll-out in a particular year between 2020 and 2035 can be formulated as equation (3) [18].
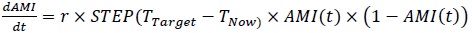 |
(3) |
The coefficient r is a correction coefficient to match the maximum AMI deployment to the target year, and the STEP function shows that the proportion of AMI roll-out keeps increasing until the target year for the entire distribution of AMI. TTarget is the year during which V2G-supported AMI is completely deployed nationwide, and TNow is the year when V2G-supported AMI is built. The STEP function can be defined using equation (4).
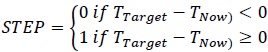 |
(4) |
Choi et al. [19], using a conjoint analysis, forecasted the number of EVs that would be disseminated by 2035 in a scenario where governmental support including tax deduction continues and the development of the related technologies progresses. By incorporating their research into the present situation in Korea, the number of EVs was estimated at about 10.3 thousand in 2015 and 1,775 thousand in 2035 (Table 2).
| Category | 2015 | 2020 | 2025 | 2030 | 2035 |
| EVs (thousand) |
10.3 | 229.1 | 638.9 | 1,166.0 | 1,775.2 |
| Passenger Cars (thousand) |
15,840 | 18,046 | 19,561 | 20,509 | 21,006 |
| Percentage of EVs (%) | 0.07 | 1.27 | 3.27 | 5.69 | 8.45 |
The peak load growth caused by EVs based on the assumed forecast has been calculated and is shown in Fig. (2). Without SG utilization, the peak load increase caused by EVs is 3,888 MW for the year 2035 in Case 1. The peak load is increased by 5,183 MW in Case 4 and by 6,479 MW in Case 7 in 2035. However, in the cases of high SG utilization such as Case 3, Case 6, and Case 9, the peak load increments remain at 586 MW, 1,882 MW, and 3,187 MW, respectively. These amounts are roughly 3,302 MW less than the peak load increment when SGs are not utilized (Fig. 2).

3. GENERATION MIX AND THE RELATED IMPACTS ON COST AND CARBON EMISSIONS
3.1. WASP Model and Major Assumptions
The Wien Automatic System Planning (WASP) model was originally developed in 1972 for the IAEA by the Tennessee Valley Authority and the Oak Ridge National Laboratory in the USA to analyze the economic competitiveness of nuclear power in comparison to other sources of electricity generation in meeting electricity requirements of a country or region in the medium- to long-term period [18]. WASP is continuously upgraded by the IAEA and is currently available as version 4. WASP determines the generating system expansion plan that meets demand at minimum cost while satisfying certain user-specified constraints for the system. The objective function (Bj) of the optimization problem in WASP is expressed in equation (5) [37].
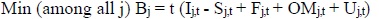 |
(5) |
where j is the alternative expansion path (program), t is the year of the study period (t = 1,2,...,T), T is the length of the study period, I is the investment (capital) costs, S is the salvage value, F is the fuel cost, OM represents the operation and maintenance costs, and U is the unserved energy cost, with all costs being discounted to a reference year at the annual discounting rate.
The input data for the WASP model are load forecast, discount rate, Loss Of Load Probability (LOLP) as a constraint, and technical and economical characteristics of existing and candidate power plants such as investment cost, fuel cost, OM costs, heat rate, and Forced Outage Rate (FOR). The output data of the WASP model are build schedule, generation, fuel consumption, costs, and emissions.
The target year that this study analyzed is 2035 and nine cases shown in Table 1 were examined. Additionally, the baseline case in which the deployment of EVs and the effect of SGs are not reflected was also examined.
To understand the electric power demand, the demand forecast in the 2nd Korean Energy Master Plan (2014-2035), the forecast of EV electricity consumption (GWh) [19], and the forecast of peak load (MW) in accordance with EV deployment and SG application were applied. The electricity consumption in Cases 1~9 was assumed to be similar. This was because the SG does not reduce the demand for the use of EVs although it does play a role in reducing or migrating peak load increases by EV charging. As EV charging costs become lower, the demand for EV use can be enhanced. This study applied only the changes of peak load caused by SGs.
In addition to the demand for electricity, the remaining input data used for the WASP model were provided by the 2015 7th Basic Plan for Long-term Electricity Supply and Demand (2015-2029) [38]. The WASP model was set to produce a cost-minimizing plan that satisfies the system reliability standard of the LOLP 0.3 day/year and a reserve margin of around 22%. The discount rate was set at 5.5%. These criteria were derived from the 7th Basic Plan for Long-term Electricity Supply and Demand (Table 3).
| Category | Year | Average Growth Rate (%) | ||||
|---|---|---|---|---|---|---|
| 2015 | 2020 | 2030 | 2035 | |||
| Consumption (GWh) |
Baseline | 489,595 | 588,352 | 664,229 | 695,040 | 1.77 |
| Cases 1-9 | 489,616 | 588,829 | 666,918 | 699,325 | 1.80 | |
| Peak Load (MW) |
Baseline | 82,478 | 97,261 | 113,548 | 120,425 | 1.91 |
| Case 1 | 82,501 | 97,763 | 116,101 | 124,313 | 2.07 | |
| Case 2 | 82,493 | 97,595 | 115,107 | 122,690 | 2.00 | |
| Case 3 | 82,486 | 97,427 | 114,113 | 121,067 | 1.94 | |
| Case 4 | 82,508 | 97,930 | 116,952 | 125,608 | 2.12 | |
| Case 5 | 82,501 | 97,762 | 115,921 | 123,958 | 2.06 | |
| Case 6 | 82,493 | 97,594 | 114,890 | 122,307 | 1.99 | |
| Case 7 | 82,516 | 98,097 | 117,804 | 126,904 | 2.18 | |
| Case 8 | 82,508 | 97,929 | 116,773 | 125,253 | 2.11 | |
| Case 9 | 82,501 | 97,761 | 115,742 | 123,603 | 2.04 | |
The 2035 capacities of some power sources were preliminarily fixed. In the analysis fixing the nuclear power capacity, 29% of total capacity in the baseline case was used as the nuclear power capacity in all cases because the 2nd Korea Energy Master Plan, which was made in January 2014, set the percentage of nuclear power plants in 2035 as 29%. The percentage of renewable energy is in agreement with the figure provided by the 2nd Korea Energy Master Plan (Table 4) [39].
| Category | Nuclear 1,400MW | Nuclear 1,500MW | Coal 500MW | Coal 1,000MW | LNG 450MW | LNG 900MW |
|---|---|---|---|---|---|---|
| Investment cost (thousand won/kW) |
2,378 | 2,396 | 1,616 | 1,494 | 1,115 | 904 |
| fuel cost (won/Gcal) | 1,776 | 1,776 | 16,987 | 16,987 | 76,736 | 76,736 |
| OM cost (thousand won/kW/month) | 11.27 | 10.91 | 4.41 | 3.88 | 3.8 | 2.78 |
| heat rate (kcal/kWh) | 2,365 | 2,375 | 2,036 | 1,978 | 1,568 | 1,540 |
| FOR (%) | 5.3 | 5.3 | 4.7 | 4.7 | 5.8 | 5.8 |
There are some reasons why power source shares must be preliminarily reflected. Nuclear power has the most limitations in terms of power plant construction and the associated huge construction costs, long construction periods, and difficulty in securing a building site. The number of nuclear power plants estimated using WASP can be much higher than that of actual constructions because of the low unit cost for power generation. In addition, the construction period of a nuclear power plant is more than 10 years and the plants currently planned or under construction can be incorporated by 2020. It is important that these aspects are reflected. As for renewable energy sources, it is necessary to determine the preliminary forecasts of the installed capacity and generated electric power of renewable energy and then make a residual load duration curve deducting the renewable energy sources.
3.2. The Changes in Generation Mix (GWh) Caused by EV Deployment and the Analysis of the Effect of SGs
According to the analysis, the baseline case showed that the total installed capacity is 147,516 MW, as presented in Table 5. The capacity share of nuclear power plants and natural gas-powered plants is 29%, and the capacity share of coal powered plants is 32.6%. The installed capacity of Case 1 reflects the 2035 scenario where EVs are disseminated by government support, but without the effect of SGs. In Case 1, nuclear power capacity was also fixed as 42,829MW, which is 29% of the share in the baseline case. As EVs cause the peak load to increase, the total installed capacity is expanded to 151,516 MW, and the share of nuclear power in terms of installed capacity decreased to 28.3%. The capacity by power supply from Case 1 was applied to Cases 2 to 9, not reflecting the effect of SGs on the changes of the installed capacities. This is because, by fixing the installed capacity mix (MW), the changes in the power generation mix (GWh) due to SG utilization can be examined, in addition to the generation costs and CO2 emissions.
| Case | Nuclear | Coal | Gas | Renewables1 | Others | Total |
|---|---|---|---|---|---|---|
| Baseline | 29.0 | 32.6 | 29.0 | 5.4 | 4.0 | 147,516 |
| 1-9 | 28.3 | 34.4 | 28.2 | 5.3 | 3.9 | 151,516 |
Table 6 shows how the generation mix varies in the nine cases in addition to the baseline case. The total power generation is 756,963 GWh in the baseline case and increases to 874,516 GWh in Case 1. This result is attributed to the increase in electric power demand as EVs are disseminated. Overall, the shares of coal and natural gas powered generation are increased in Cases 1 to 9 compared to the baseline case. However, all the nuclear power generation in Cases 1 to 9 is fixed as 37% due to the similar total demand and fixed installed capacity regardless of the degree of SG utilization. Cases 1 to 3 show that with a higher degree of SG utilization, more coal is produced, but less natural gas is produced. The same result is derived for Cases 4 to 6 and 7 to 9. By applying the effects of SGs, the peak load lessens and the use of natural gas power plants as a power generation unit for peak load becomes lower. The coal powered generation, in contrast, increased to replace the decreased natural gas-powered generation due to the SG utilization. This phenomenon occurs strongly in Cases 3, 6, and 9, where the degree of SG utilization is the highest.
| Case | Nuclear | Coal | Gas | Renewables | Others | Total |
|---|---|---|---|---|---|---|
| Baseline | 41.9 | 38.0 | 7.8 | 12.0 | 0.3 | 756,963 |
| 1 | 37.0 | 40.8 | 11.4 | 10.4 | 0.4 | 874,516 |
| 2 | 37.0 | 40.9 | 11.2 | 10.4 | 0.4 | 874,762 |
| 3 | 37.0 | 41.0 | 11.1 | 10.4 | 0.4 | 875,034 |
| 4 | 37.0 | 40.7 | 11.5 | 10.4 | 0.4 | 874,329 |
| 5 | 37.0 | 40.9 | 11.3 | 10.4 | 0.4 | 874,566 |
| 6 | 37.0 | 41.0 | 11.2 | 10.4 | 0.4 | 874,818 |
| 7 | 37.0 | 40.7 | 11.5 | 10.4 | 0.4 | 874,165 |
| 8 | 37.0 | 40.8 | 11.4 | 10.4 | 0.4 | 874,376 |
| 9 | 37.0 | 40.9 | 11.3 | 10.4 | 0.4 | 874,608 |
Table 7 below illustrates the average unit cost and CO2 emission by analyzed cases. The average unit cost was calculated by multiplying power generation by power source from the WASP analysis by the unit cost, adding them, and dividing the calculated number by total generation. The settlement price in 2014 was premised as the unit cost by power source. Some details of the settlement price (won/kWh) of major power supply are as follows: nuclear 54.96, coal 65.79, oil 221.32, and LNG 162.34. The greenhouse gas emission was drawn through the WASP-IV model.
| Case | Baseline | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Cost per kWh (Won/kWh) | 79.42 | 82.19 | 82.09 | 81.99 | 82.19 | 82.17 | 82.07 | 82.34 | 82.26 | 82.15 |
| - | - | Compared to Case 1 | Compared to Case 4 | Compared to Case 6 | ||||||
| - | - | - | -0.1 | -0.2 | - | -0.02 | -0.12 | - | -0.08 | -0.19 |
| CO2 (million ton) | 262.1 | 334.3 | 334.8 | 335.3 | 333.9 | 334.4 | 335.0 | 333.6 | 334.0 | 334.5 |
| - | - | Compared to Case 1 | Compared to Case 4 | Compared to Case 6 | ||||||
| - | - | - | 0.5 | 1.0 | - | 0.5 | 1.1 | - | 0.4 | 0.9 |
In Case 1, the average unit cost of power generation increases by about 2.9 won/kWh compared to the baseline case. However, in Cases 2 and 3 that reflect the SG effect, it decreases slightly. Meanwhile, the CO2 emissions are higher when the SG effect is expressed. Cases 4~6 and Cases 7~9 are also similar. It is because the share of natural gas-powered generation decreases and that of coal increases. As long as the proportions of nuclear power and renewable energy remain limited, the peak load reduction or migration has the effect of increasing the CO2 emissions in the power generation sector.
3.3. The Changes in Installed Capacity Mix (MW) and the Effect of SGs
3.3.1. Fixing only Nuclear Power Capacity
This section investigates the installed capacity mix with consideration of the peak load reduction by SGs as well as the forecast of EV dissemination. The installed capacity of nuclear power in 2035 was fixed at 42,829MW, which is 29% of the total baseline capacity. As SGs are utilized more, by decreasing the peak demand, the total installed capacity decreases. However, the share of natural gas generation capacity increases gradually while the share of coal generation capacity decreases by increasingly utilizing SGs. This is because the capacity of coal generation, which is more economical than LNG power, increases to meet the increased power demand due to the diffusion of EVs when SGs are not utilized in cases such as 1, 4, and 7; however, there is less need to build coal-powered plants with higher SG utilization such as cases 3, 6, and 9.
The generation share also shows similar characteristics with the capacity share change (Table 8). As SGs are more utilized, the coal generation share falls, but the natural gas generation share rises. The nuclear power generation is fixed at 37.0% because the generation has a maximum capacity factor as a baseload power plant and similar capacity leads to similar generation.
| Case | Nuclear | Coal | Gas | Renewables | Others | Total |
|---|---|---|---|---|---|---|
| Baseline | 29.0 | 32.6 | 29.0 | 5.4 | 4.0 | 147,516 |
| 1 | 28.3 | 34.4 | 28.2 | 5.3 | 3.9 | 151,516 |
| 2 | 28.6 | 33.5 | 28.6 | 5.3 | 3.9 | 149,516 |
| 3 | 29.0 | 32.6 | 29.0 | 5.4 | 4.0 | 147,516 |
| 4 | 27.9 | 35.2 | 27.8 | 5.2 | 3.8 | 153,516 |
| 5 | 28.3 | 34.4 | 28.2 | 5.3 | 3.9 | 151,516 |
| 6 | 28.6 | 33.5 | 28.6 | 5.3 | 3.9 | 149,516 |
| 7 | 27.7 | 35.7 | 27.7 | 5.2 | 3.8 | 154,516 |
| 8 | 28.1 | 34.8 | 28.0 | 5.2 | 3.9 | 152,516 |
| 9 | 28.5 | 33.9 | 28.4 | 5.3 | 3.9 | 150,516 |
As the power generation by natural gas-powered plants amplifies, the average unit cost for power generation gradually rises as the degree of SG utilization becomes higher, as shown in Tables 9 and 10. However, the CO2 emissions decrease as the SG utilization degree becomes higher, because the share of coal powered generation is reduced.
| Case | Nuclear | Coal | Gas | Renewables | Others | Total |
|---|---|---|---|---|---|---|
| Baseline | 41.9 | 38.0 | 7.8 | 12.0 | 0.3 | 756,963 |
| 1 | 37.0 | 40.8 | 11.4 | 10.4 | 0.4 | 874,516 |
| 2 | 37.0 | 39.9 | 12.3 | 10.4 | 0.4 | 874,336 |
| 3 | 37.0 | 38.8 | 13.3 | 10.4 | 0.4 | 874,199 |
| 4 | 37.0 | 41.7 | 10.5 | 10.4 | 0.4 | 874,782 |
| 5 | 37.0 | 40.9 | 11.3 | 10.4 | 0.4 | 874,566 |
| 6 | 37.0 | 39.9 | 12.3 | 10.4 | 0.4 | 874,395 |
| 7 | 37.0 | 42.1 | 10.1 | 10.4 | 0.4 | 874,868 |
| 8 | 37.0 | 41.3 | 10.9 | 10.4 | 0.4 | 874,603 |
| 9 | 37.0 | 40.3 | 11.8 | 10.4 | 0.4 | 874,408 |
| Case | Baseline | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Cost per kWh (Won/kWh) | 79.42 | 82.19 | 83.16 | 84.16 | 81.32 | 82.17 | 83.13 | 80.91 | 81.78 | 82.69 |
| - | - | Compared to Case 1 | Compared to Case 4 | Compared to Case 6 | ||||||
| - | - | - | 0.97 | 1.97 | - | 0.85 | 1.81 | - | 0.87 | 1.78 |
| CO2 (million ton) | 262.1 | 334.3 | 333.0 | 327.4 | 337.5 | 334.4 | 331.2 | 339.0 | 335.8 | 332.7 |
| - | - | Compared to Case 1 | Compared to Case 4 | Compared to Case 6 | ||||||
| - | - | - | -1.3 | -6.9 | - | -3.1 | -6.3 | - | -3.2 | -6.3 |
3.3.2. Without Capacity Constraints
Note that installed capacity has been entirely or partially constrained throughout the paper. However, in this section, WASP is used without constraints of changes in the installed capacity of the power supply. First, the capacity change in Table 11 shows that nuclear power plants, with the most significant economic benefits among power generation sources, have been built to meet increasing electricity demand due to the spread of EVs. It is worth noting that as the degree of SG utilization becomes high, the share of nuclear power capacity decreases. It is because when peak demand decreases, there is no need to build additional nuclear power plants. Moreover, as SG utilization increases, the shares of coal and natural gas power capacity increased.
| Case | Nuclear | Coal | Gas | Renewables | Others | Total |
|---|---|---|---|---|---|---|
| Baseline | 29.0 | 32.6 | 29.0 | 5.4 | 4.0 | 147,516 |
| 1 | 33.3 | 29.2 | 28.3 | 5.3 | 3.9 | 151,016 |
| 2 | 32.7 | 29.5 | 28.6 | 5.3 | 3.9 | 149,516 |
| 3 | 32.0 | 29.8 | 28.9 | 5.4 | 4.0 | 148,016 |
| 4 | 34.0 | 28.9 | 28.0 | 5.2 | 3.9 | 152,516 |
| 5 | 33.3 | 29.2 | 28.3 | 5.3 | 3.9 | 151,016 |
| 6 | 32.7 | 29.5 | 28.6 | 5.3 | 3.9 | 149,516 |
| 7 | 35.3 | 28.4 | 27.5 | 5.1 | 3.8 | 155,516 |
| 8 | 34.0 | 28.9 | 28.0 | 5.2 | 3.9 | 152,516 |
| 9 | 33.3 | 29.2 | 28.3 | 5.3 | 3.9 | 151,016 |
With respect to power generation, similar characteristics shown in the change of share in the installed capacity can be found. As the SG utilization becomes high, the share of nuclear power generation decreases. On the contrary, the shares of coal and natural gas coal powered generation together increase to replace the diminished share of nuclear power generation.
The analysis of generation costs shows that as SG utilization becomes high, the share of nuclear energy, which is the most cost-effective energy source, diminishes, whereas coal and gas powered generation with relatively higher shares than nuclear energy takes greater shares, contributing to a rise in average unit cost (Table 12).
However, when compared to Table 10, it can be seen that the generation cost for each case is lowered in Table 13. It is not because of the impact of SGs, but rather the share increase of nuclear energy. It is clearly observed that CO2 emissions increase as the degree of SG utilization becomes high. In addition, as with generation cost, the absolute value of CO2 emissions was reduced compared to the values listed in Tables 7 and 10.
| Case | Nuclear | Coal | Gas | Renewables | Others | Total |
|---|---|---|---|---|---|---|
| baseline | 41.9 | 38.0 | 7.8 | 12.0 | 0.3 | 756,963 |
| 1 | 43.2 | 34.3 | 11.7 | 10.4 | 0.4 | 874,718 |
| 2 | 42.0 | 34.8 | 12.3 | 10.4 | 0.4 | 874,556 |
| 3 | 40.8 | 35.3 | 13.0 | 10.4 | 0.4 | 874,428 |
| 4 | 44.3 | 33.8 | 11.0 | 10.4 | 0.4 | 874,947 |
| 5 | 43.2 | 34.3 | 11.7 | 10.4 | 0.4 | 874,763 |
| 6 | 42.0 | 34.9 | 12.3 | 10.4 | 0.4 | 874,614 |
| 7 | 46.6 | 32.8 | 9.8 | 10.4 | 0.4 | 875,215 |
| 8 | 44.3 | 33.8 | 11.0 | 10.4 | 0.4 | 874,987 |
| 9 | 43.2 | 34.3 | 11.6 | 10.4 | 0.4 | 874,822 |
| Case | Baseline | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Cost per kWh (Won/kWh) | 79.42 | 81.87 | 82.65 | 83.49 | 81.09 | 81.85 | 82.63 | 79.55 | 81.06 | 81.82 |
| - | - | Compared to Case 1 | Compared to Case 4 | Compared to Case 6 | ||||||
| - | - | - | 0.78 | 1.62 | - | 0.76 | 1.54 | - | 1.51 | 2.27 |
| CO2 (million ton) | 262.1 | 291.3 | 297.2 | 302.9 | 285.6 | 291.4 | 297.3 | 274.0 | 285.7 | 291.5 |
| - | - | Compared to Case 1 | Compared to Case 4 | Compared to Case 6 | ||||||
| - | - | - | 5.9 | 11.6 | - | 5.8 | 11.7 | - | 11.7 | 17.5 |
4. DISCUSSION
The dissemination of EVs will lead to an increase in electricity demand. If the EV usage experiences rapid growth, especially with the support of the government, preparation for soaring power demand must also be done. This study has examined the aspects of power demand increase, particularly peak demand increase in accordance with EV roll-out in South Korea, and has verified that peak load is significantly reduced according to the degree of SG utilization. The reduction in peak load has an effect of lowering the potential disruption of power supply caused by lack of power plants and transmission and distribution infrastructure. As the efficiency in charging EV batteries and the battery capacity is improved, the beneficial effects will be enhanced.
This paper has also investigated the generation mix according to EV deployment, and how SGs affect power generation costs and CO2 emissions. The analysis showed that SGs lessen the peak load which is reduced by 3,302 MW in Case 1, Case 4, and Case 7 compared to Case 3, Case 6, and Case 9 respectively and the decrement of natural gas-powered generation, acting as a major power source for peak load supply, results in lowered generation cost. However, the increase in coal-powered generation results in the increase of CO2 emissions in the power sector. For example, in Case 3 where SG utilization is high compared to Case 1 which does not use the SGs, the unit cost decreases by 0.8 KRW/kWh but CO2 increases by 1 million tons. Thus far, the positive effects of SGs have been emphasized in that they decentralize the time-slots for EV charging and heighten the stability of the power supply by using V2G when the electricity supply is tight. Yet, the increased dependence on coal-powered generation increases CO2 emissions in the power sector. These conflicting effects should be taken into account when considering the effects of SGs.
In the analysis of the change in installed capacity mix with consideration of the peak load reduction by SGs, this paper has examined installed capacity, power generation, and change in CO2 emissions with two methods. First, an analysis was carried out with the condition that nuclear capacity is fixed, while the other sources are not. From the results, the shares in coal power capacity and power generation decreased as the SG utilization becomes high. On the contrary, the shares of natural gas power capacity and power generation increased. Ultimately, the increase of SG utilization facilitated a rise in average unit cost, lowering the total amount of CO2 emissions. Table 10 shows that the unit costs increase by 1.78 ~ 1.97 KRW/kWh and CO2 decreases by 6.3 ~ 6.9 million tons for Case 3, Case 6 and Case 9 compared to Case 1, Case 4, and Case 7. It resulted from the fact that although the SG utilization increases, electricity demand remains unchanged and peak demand decreases, making it possible to avoid construction of additional coal-fired power plants. Second, the power mix is drawn based on the economic feasibility without capacity constraint on energy sources including nuclear power plants. The results reveal that new nuclear power plants are built to meet increasing electricity demand influenced by the dissemination of EVs, lowering average unit cost and the absolute value of CO2 emissions. However, unit generation cost and CO2 emissions tend to increase as SG utilization becomes high. Table 13 shows that the unit costs increase by 1.54 ~ 2.27 KRW/kWh and CO2 also increases by 11.6 ~ 17.5 million tons for Case 3, Case 6 and Case 9 compared to Case 1, Case 4, and Case 7. This is because SG utilization leads to increasing dependence on fossil fuel generation by avoiding construction of new nuclear facilities.
Consequently, it cannot be seen from all cases that high SG utilization always reduces both average unit cost and CO2 emissions together. In the case of South Korea, the minimum load reaches a little more than 40%. To reduce the increment in power generation costs and CO2 emissions caused by EVs through SGs, the proportion of generation capacity from clean and low-carbon energy sources must surpass the minimum load. Although the share of nuclear power capacity in South Korea is 22% (as of the end of 2016), ranked third in the world, the total installed capacity of nuclear power and renewable energy does not reach the level of the minimum load. Thus, the additional demand for electric power from EVs eventually increases power generation from fossil-fuel sources. The differentiation and contribution of this study are summarized as follows:
- This study is valuable in that it examines comprehensively the impacts of EVs on the electric power system in terms of electricity supply and demand while presenting economic and environmental impacts in different scenarios. In addition, this study shows significant differentiation because it considers the change of the generation capacity mix when analyzing the influence of EVs on the electric power system while the existing researches focus on the change of power generation mix without considering the change of the installed capacity mix. This study has used the authoritative tool WASP-IV to consider the variation of power capacity mix due to the spread of EVs.
- This study distinguishes the case where the proportion of nuclear power capacity is fixed beforehand regardless of WASP-IV model operation and the case where the proportion is not fixed but derived through the model operation. This study has differentiation in that the cases provide a basis to suggest implications for both countries that determine the proportion of nuclear power capacity under top-down decision-making system and countries that autonomously decide the proportion on the market.
- This study has a contribution in that it shows the importance of considering the minimum load. The results of this study have showed that if the clean and low carbon power sources do not exceed the minimum load, it would be difficult to meet the economic and environmental requirements at the same time even if the EV charging is managed through the SGs. When the proportion of power generation from clean energy sources does not meet the minimum load, coal-powered plants will also need to be operated even while EVs are charged over-night when power demand is low. Increasing the share of power generation from clean energy sources to a level higher than that of the minimum load will allow EVs to become an eco-friendly means of transportation. On the other hand, even though the proportion of clean energy capacity in the whole country does not exceed the minimum load, there is a case where renewable energy generation such as solar power and wind power is curtailed due to constraints on the transmission and distribution network. There is a need to develop technologies that efficiently utilize such renewable energy through EVs without being curtailed.
CONCLUSION AND IMPLICATIONS
This study comprehensively examined the changes of power supply and demand and their effects in accordance with the degree of SG utilization, based on a scenario for the projection of EV deployment in South Korea to understand the EV management effects deeply using SGs in the electric power sector. The main findings are as follows:
- When the management of EV charging load and V2G is enabled through SGs, it is possible to lessen the peak load increase by EVs and maintain the stability of the power supply. For instance, the peak load is reduced by 3,302 MW in Case 3 where SG utilization is high compared to Case 1 where the SGs are not utilized. As the efficiency in charging EV batteries and the battery capacity are improved, the beneficial effects will be enhanced.
- As the power capacity mix is fixed, SGs induce a decline in generation costs by reducing the demand for natural gas as a peak load power source and high-cost fuel. However, this expands the use of coal powered plants, thereby increasing the CO2 emissions in the power sector (see Table 7). These conflicting effects should be taken into account when considering the effects of SGs.
- As the SG utilization becomes high, the amount of CO2 emissions is reduced and unit generation cost increases, under the condition that nuclear capacity is fixed, while other forms of power generation are not (see Table 10). In addition, high SG utilization led to an increase in both average unit cost and CO2 emissions under the assumption that the installed capacity of power generation sources was not fixed (see Table 13).
- For SGs to play a positive role in the management of EVs, the share/size of cost-effective and clean power generation source must be increased. At this point, it is worth noting the minimum load. If the share of cost-effective and clean power generation sources is above the minimum load, the utility of SGs increases, reducing the average unit cost and CO2 emissions together. Understanding this characteristic is very important for related SG and EV policy-making.
This study has quantitatively investigated the effects of EV charging management through SGs on the power demand and supply. This study is especially differentiated since it considers the change of the generation capacity mix as well as the change of power generation mix. This study also deals with various cases to provide useful implications in different countries and regions. This study has also a contribution since it shows the importance of considering the minimum load that many people take little account of for the management of EVs.
A limitation of the present research is that it examines the EV charging management only in terms of time and not geographical location. That is, the functional effect of lessening concentrated EV charging in a specific area should be looked at in view of the dispersion of EVs and the capacity of distributed power by regions. When geographical dispersion and the time-slot shift of EVs are measured together, the complexity of the issue increases and a new research approach would be required. The ancillary services of V2G such as providing spinning reserve should also be considered.
| Symbol | Meaning | Unit |
|---|---|---|
| PVEH | maximum electric power transferable through V2G | KW |
| ES | battery-stored energy available as direct current transferable to an inverter | kWh |
| dD | driving distance when the battery of an EV is fully charged | km |
| dRB | minimum range buffer driving distance required for a driver | km |
| ηPEV/PHEV | average driving efficiency of pure EVs (PEVs) and plug-in EVs (PHEVs) | kWh/km |
| ηINV | efficiency of the inverter where the direct current of the battery converts into alternating current | % |
| tDISP | time that the stored energy in EVs is dispatched | hour |
| fEV (G2V) | percentage of EVs connected to power grid for charging | % |
| fEV (V2G) | percentage of EVs connected to power grid for discharging | % |
| PLG2V/V2G | effect of EVs on the peak load when considering G2V and V2G | KW |
| δ | coefficient determined by multiplying the proportion of EVs charging during peak load time by the average charging electric power (kW) of each EV | % |
| ε | coefficient determined by multiplying the proportion of EVs discharging during peak load time by the average discharging electric power (kW) of each EV | % |
| NPEV/PHEV(t) | number of EVs at time (t) | - |
| TTarget | year during which V2G-supported AMI is completely deployed nationwide | year |
| TNOW | year when V2G-supported AMI is built | year |
| Bj | objective function of the optimization problem in WASP | - |
| I | investment (capital) cost | - |
| S | salvage value | - |
| OM | operation and maintenance cost | - |
| F | fuel cost | - |
| U | unserved energy cost | - |
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


