All published articles of this journal are available on ScienceDirect.
Improving Population Demand Estimation with Transit Chaining Breaks
Abstract
Background:
Data mining of smart card data collected through AFC systems have proved useful in estimations of public transport demand. Whereas most estimations of demand are made by analyzing transit orientations or destinations of unchained transits. However, organization of bus or metro routes compels riders to make a lot of unnecessary transfers, and the transfer points are neither reflective of population’s actual orientations nor of their destinations.
Aims and Objectives:
The objective of this paper is to improve estimations of population demand by identifying transfer activities of riders using public transportation. Durations and displacements of transit chaining breaks are to be check in judging the transfer activities.
Boarding stops for making transfers are ruled out as transportation demand estimation. The effectiveness of the new approach entailing the use of transit chaining breaks is also to be evaluated based on the calculation of Pearson product-moment correlation coefficients for assessing the correlation between transportation estimation and population distribution.
Result and Conclusion:
Durations and displacements of transit chaining breaks could be used to identify transfer activities. The use of the transit chaining approach reduces the occurrence of false demand, resulting in the estimation being more objective in relation to the population.
The results of the study indicated that the inclusion of transit chaining breaks leads to more accurate estimations of public transport demand within a population.
1. INTRODUCTION
Reliable estimations of transit demands can facilitate improvements in public transport [1]. Traditional estimations of the demand for public transportation are based mainly on surveys [2], which are expensive and tedious to conduct [3]. The use of smart cards enabling Automated Fare Collection (AFC) is becoming increasingly popular [4], and data collected through AFC systems have proved useful in transit planning [5]. Whereas most estimations of demand are
made by analyzing transit orientations or destinations [3], in practice, transfer points are neither reflective of transit riders’ actual orientations nor of their destinations. The practical organization of bus or metro routes compels riders to make unnecessary transfers. Consequently, an investigation of how such unnecessary transfers can be avoided is pertinent [6].
Because transit OD (Origin–Destination) pairs are not ideal for use in estimations of demands for transportation, some researchers have explored the use of trip-chaining approaches, according to which transits are viewed as complete journeys. Trip chaining approaches provide researchers with useful information [7], and the availability of comprehensive profiles of riders’ transit behaviors enables modelers and public facilities planners to improve estimations of demands for transportation [2]. The trip-chaining approach basically entails connecting sequenced legs of the trips of smart card holders and listing their public transport trips. Particular criteria, such as whether passengers’ boarding stops are close to the stops at which they previously alighted, and whether a reasonable amount of transfer time exists, are used to identify transfers made between transits. However, the reliability of these methods has not been well investigated [8], and applications of the chaining approach have not been adequately explored.
This study is aimed at investigating how transit chaining and Transit Chaining Breaks (TCBs) can be used to identify transfers made during riders’ use of public transportation. Moreover, based on our findings, we discuss whether and how the adoption of this approach could lead to improved estimations of population demand in public transport.
2. METHODS
2.1. Description of the Transit Chaining Breaks approach
A trip chain comprises a series of trips made by a rider on a daily basis, and the entailed sequence of trips demonstrates the rider’s traveling behavior [9]. The transit chaining method is normally applied by connecting a passenger’s trip legs [8]. Some public transportation riders may arrive directly at their shopping or work destinations, whereas others may make transfers immediately after alighting at their stops. Still others may commence their transit after reaching a stop as a result of taxi rides or simple walks. Regardless of the commuting behaviors of riders, transit chains comprise single transits connected by breaks. AFC systems record the boarding and alighting times of transit riders in some cities, thereby generating geo-tagged transit data that enable the calculation of displacements and trip durations, which are important attributes of Transit Chaining Breaks (TCBs). Fig. (1) depicts a cardholder’s transit chain. Point A denotes the first boarding station; point B denotes the first alighting station, and so forth. Displacements occur between the previous stop at which the rider alights and next boarding stop. All three breaks have particular durations, but the third break does not entail a displacement.
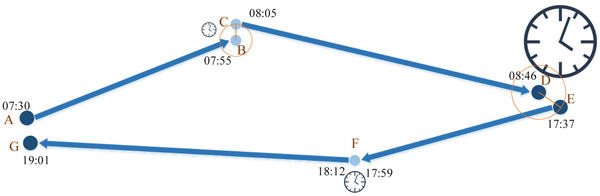
A key issue addressed in this study focuses on whether TCBs are transfers or actual destinations. Transfers are treated as an unnecessary demand generated by an imperfect transportation system. TCBs have specified durations, and displacements are not accounted for in estimations of demands for transportation.
2.2. TCB Duration
TCB duration is defined as the time that lapses between the swiping of a rider’s smart card when boarding at a stop and his or her previous alighting. It includes the duration of the following activities of the rider: checking out, walking between stations, and finally getting into the public transport system and checking in with his/her smart card. The duration of transit number n of a cardholder is calculated as follows:
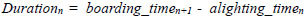 |
(1) |
where boarding_timen+1 denotes the boarding time for transit number n and alighting_timen denotes the alighting time for transit number n+1.
Many dimensions need to be considered to determine the purposes of transit. However, an analysis can be performed using the threshold time of transfer within a public transport system to determine whether a TCB is a transfer. The time required to make transfers varies, and it is difficult to ascertain the required transfer times using the smart card data alone [6]. Previous studies have shown that the threshold transfer time may vary, usually ranging from 30 minutes to 60 minutes, and even extending up to 90 minutes [10-12].
2.3. TCB Displacement
TCB displacement is defined as the distance between the boarding station and the previous station at which the rider alights. Because the lengths of actual routes are complex and difficult to ascertain, here great-circle distances between boarding stations and previous alighting stations are treated as TCB displacements, and the displacements are calculated using the following haversine formula:
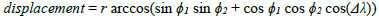 |
(2) |
where ϕ1, λ1, and ϕ2, λ2 denote the respective geographical latitude and longitude, in radians, of the boarding station and the previous alighting station, Δλ is the absolute difference between λ1 and λ, and r is the radius of the Earth.
Previous studies have shown that the transfer type TCB distance can range from 400 m to 1,100 m [8, 13]. On its own, the TCB displacement does not indicate whether it is a transfer point. Displacements in combination with TCB durations are more effective in identifying transfer activities.
2.4. Identification of Transfer Activity
Here, we introduce the duration-displacement matrix of TCBs. Based on this matrix, the following criteria were used to determine transfer activity relating to TCBs: (i) the TCB duration is too short for implementing activities other than transfers and (ii) the displacement occurs within a walkable distance.
2.5. Verification and Validation of the Approach
A residential population zone is considered to be positively related to the demand for public transport [14]. The test criterion was the consistency of the demand estimation with regard to the distribution of the population investigated in this study. The demand estimation of zone number i can be expressed as:
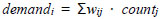 |
(3) |
where demandi and countj denote the outcome of the demand estimation for zone i and the assumed demand of transit station number j. The value of wij is 0 or 1 depending on whether station number j is located in zone i.
Control group: Daily boarding volumes at stations were treated as public demand, and the counts were projected into cell zones based on a population survey. Array Xcontrol = [demand1, demand2, demand3, … demandi]control, where demandi denotes the need for public transportation in zone i.
Test group: After excluding transfer TCBs, the counts were projected on to population survey zones. Array Xtest = [demand1, demand2, demand3, … demandi]test.
Pearson product-moment correlation coefficients (Pearson) were calculated for population arrays in relation to the demand arrays to measure how the estimations generated by new method were in relation to the population. The formula used for calculating Pearson was:
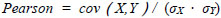 |
(4) |
where cov denotes covariance and σX and σY are standard deviations of X and Y.
Y = [population1, populaton2, … populationi], where populationi is a population in zone i.
If Pearson(control) < Pearson(test), then the TCB method can be considered to be more objective than the non-TCB approaches.
3. CASE STUDY AND RESULTS
3.1. Data Description
An assessment of transit data for Beijing’s bus and metro systems revealed that there was very little change in traffic volumes at each station on workdays. For example, fluctuations in card checking counts at the 100 busiest stations in Beijing were less than 5% during the period August 15–19, 2016. For this study, the transit logs for Beijing’s bus and metro systems were obtained for August 17, 2016, as they yielded typical data for workdays. Each entry contains card numbers, boarding stations, boarding times, alighting stations, and alighting times. A total of 13,000 bus stations and 345 metro stations were covered in the study. Analysis of the data indicated that there were 3,586,286 transit chains with 6,351,735 TCBs.
3.2. Duration-displacement Matrix
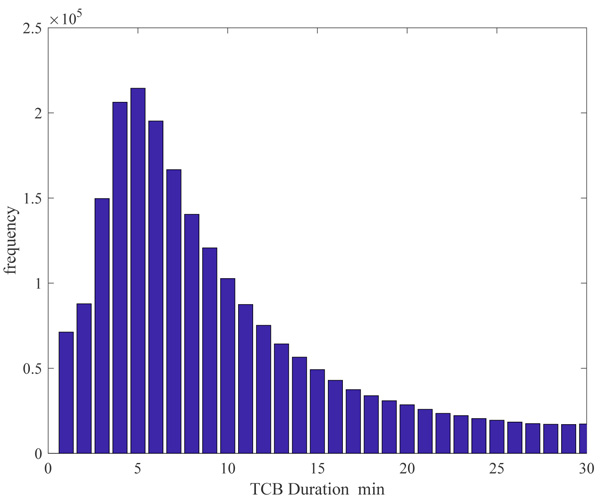
Of the 6.35 million TCB displacements that were identified, 1.7 million were 0 km in distance, indicating that riders’ boarding stations were also their final alighting stations. A graphic depiction of the duration-displacement matrix (Fig. 2) clearly reveals the relation between TCB displacements and durations. Fig. (2) shows that most transfers were made within a displacement distance of 2 km and durations were less than 15 minutes (breaks with displacements of 0 km were not depicted).

A total of 6.3 million displacements were less than 2 km. Consequently, we set a TCB displacement of 2 km as the transfer threshold distance. Fig. (3) indicates that 20 minutes was a reasonable transfer threshold time for identifying transfer activities.
3.3. Identification of Transfers
Table 1 shows the 10 stations where the most transfers took place. Those stations were generally treated as major demand sources. However, not all transfer activities occurring at those stations should be considered to indicate a demand for public transport.
| Station Name | Transfer Count |
|---|---|
| Dongzhimen | 16,788 |
| Liuliqiao East | 16,708 |
| Xizhimen | 15,599 |
| Guomao | 13,702 |
| Sanyuanqiao | 12,599 |
| Dongzhimen hub | 7,247 |
| Yuquanlu | 6,476 |
| Jishuitan | 6,438 |
| Beijing West Station | 6,148 |
| Huoying | 5,953 |
3.4. Validation of the Approach
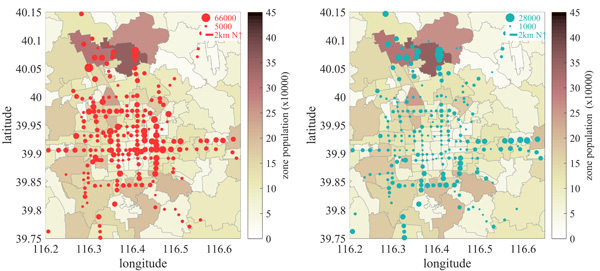
Beijing was divided into 306 sub-district zones in China’s sixth national population census implemented in 2010. A traditional estimation method basing on transit OD pairs (Xcontrol) as well as a method entailing the use of TCBs (Xtest) were conducted. Calculated Pearson product-moment correlation coefficients of Pearsoncontrol and Pearsontest indicated that the transit chaining approach generated higher correlations between X (transport demand estimation) and Y (population distribution), especially in the most active zones (Table 2). The use of the transit chaining approach reduced the occurrence of false demand, resulting in the estimation being more objective in relation to the population (Fig. 4).
| – | Pearson(control) | Pearson(test) |
|---|---|---|
| top 10 active zones | 0.48 | 0.87 |
| 200 active zones | 0.58 | 0.65 |
| all 306 zones | 0.69 | 0.72 |
4. DISCUSSION
The main contribution of this study lies in its elaboration of a TCB approach and its demonstration that this approach could improve the objectivity and reliability of estimations of transportation demands. A TCB duration-displacement matrix was developed and applied to identify transfer activities. One of the advantages of using this approach is that it yields a more reliable estimation of transportation needs. In traditional estimations, transfers are incorporated into transport needs. Consequently service shortage areas are less prominent and more difficult to identify. However, a limitation of this study was that it depended on data extracted from transit logs. Consequently, further studies are required to confirm the improvements before utilizing this method in transport policy making.
CONCLUSION
Information on TCB durations and displacements could be used to identify transfer activities. The findings of the study suggest that the application of the transit chaining method in estimations of the demand for public could yield more reliable and objective results compared with those obtained using transit OD pair-based estimations.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The authors wish to thank Yangxue from the Beijing Transportation Information Center for providing us the data for the study. We thank Radhika Johari from Liwen Bianji, Edanz Editing China (www.liwenbianji.cn/ac), for editing the English text of a draft of this manuscript We would also like to thank the financial support from the Strategic Priority Research Program of the Chinese Academy of Sciences, Grant No.XDA19040402.


