All published articles of this journal are available on ScienceDirect.
Application of Various Multiple Criteria Analysis Methods for the Evaluation of Rural Road Projects
Abstract
Introduction:
Ex-ante evaluation of rural road projects is important for proper utilisation of scarce financial resources. In recent years, several multiple criteria analysis methods have been applied for the evaluation of transportation projects.
Methods:
Here we compare three multi-criteria methods (i.e. TOPSIS, MOORA, and PROMETHEE) in ranking rural roads. The criteria and weightage were identified with an expert questionnaire survey and the decision matrix was obtained from a field survey of four rural roads of Nepal. These data demonstrate the successful application of various multi-criteria analysis methods for the evaluation of rural road projects with sustainable indicators.
Results:
The results of multi-criteria methods depend upon the value of performance measures, weightage, normalization, and aggregation procedures.
Conclusion:
We also concluded that the multi-criteria methods used (i.e. TOPSIS, MOORA, and PROMETHEE), in which weightage is derived using robust methods (e.g. AHP) and precise measurement of criteria of rural roads, in general return similar rankings.
1. INTRODUCTION
At the present time, almost 46% of 7.349 billion of the world’s population are still living in rural areas [1]. Due to the need of rural areas for development, rural transportation projects’ demand is high. On the other hand, the cost of the investment per km per person of rural roads is very high as compared to the urban roads. Furthermore, financial resources for rural roads, especially in developing countries, are insufficient as compared to demand. The “lack of rural access roads has killed the dreams and resilience of those who may have chosen to live in the villages” [2]. Thus, ranking or selecting the most important rural roads is a very important issue for planners, decision makers, politicians and other stakeholders. Numerous types of evaluation methods are applied in ranking or selecting rural road projects. “Cost – Benefit Analysis (CBA) has been a widely used tool in decision making on transport projects in many countries for many years” [3]. Nevertheless, financial costs or benefits are not sufficient to evaluate the sustainability of infrastructure projects. Since the Earth Summit held on Rio de Janeiro, Brazil, on 1992 sustainability has “become perceived as a combination of three dimensions or ‘pillars’, namely, the environmental (ecological), economic, and social dimensions” [4] of any infrastructure project. These economic, social, and environmental criteria, and their corresponding sub-criteria, are measured either quantitatively or qualitatively. The criteria and sub-criteria might have difference importance and even conflict each other. CBA cannot cover all these three dimensions [5]. Hence, in the frame of this paper, a suitable multi-criteria method shall be identified and applied for the evaluation of rural transportation projects.
There are several multi-criteria methods applied in rural transportation projects. Broadly, the multi-criteria methods are classified as following: a) priority or utility methods, such as the Multi-Attribute Utility Theory / Multi-Attribute Value Theory (MAUT/MAVT) and the Simple Multi-Attribute Rating Technique (SMART); b) outranking methods such as the Elimination and Choice Expressing Reality, or “ELimination Et Choix Traduisant la REalité” (ELECTRE) in French, and the Preference Ranking Organization Method for Enrichment of Evaluations (PROMETHEE); c) distance based methods such as the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) and the Multi-criteria Optimization and Compromise Solution, or Višekriterijumsko Kompromisno Rangiranje (VIKOR) in Serbian; d) mixed and other methods such as the linear additive method, the Analytic Hierarchy Process (AHP), the Likert scale, the fuzzy-TOPSIS, the fuzzy-VIKOR, etc [6].
This study examines three multi-criteria methods (viz. TOPSIS, Multi-Objective Optimisation on the basis of Ratio Analysis [MOORA], and PROMETHEE) with the application of a real case study in Nepal. The strength of TOPSIS is that it is easy to implement having an understandable principle, it is applicable when exact and total information is collected, it considers both the positive and negative ideal solutions, and it provides a well-structured analytical framework for alternatives ranking [7]. TOPSIS and MOORA methods are very simple and do not need the use of sophisticated software. Furthermore, a free academic software is available for PROMETHEE. For this reason, these three multi-criteria methods: TOPSIS, MOORA, and PROMETHEE were applied in order to aggregate the performance parameters. The study presents a brief overview of the application of these multi-criteria methods and the methodology applied in this study as follows. After that, the analysis and results are presented and a discussion follows. Finally, the conclusions derived from the study are presented.
2. OVERVIEW OF MULTIPLE CRITERIA ANALYSIS METHODS FOR EVALUATION
Different researchers/practitioners have used different multi-criteria analysis methods for combining the value of performance parameters. The study by Mardani et al. (2015) showed that among the different Multi-Criteria Analysis (MCA) methods (100%), AHP (32.57%), hybrid Multiple-Criteria Decision-Making (MCDM) (16.28%), aggregation Decision-Making (DM) Methods (11.70%), TOPSIS (11.4%), ELECTRE (8.65%), PROMETHEE (6.62%), and VIKOR (3.56%) were applied in different kinds of multi-criteria decision-making problems between 2000 to 2014 [8]. However, “there are no universally-accepted approaches. Each method stands on its own background and principles” [9]. Otun (2016) applied a decision making framework using concordance/discordance analysis within a multi-criteria decision support system to a process of selecting a ward (out of eleven) to be provided with a rural road in a local government area in Nigeria [10]. Joerin et al. (2001) applied Geographic Information System (GIS) and outranking multi-criteria analysis for land suitability assessment [11]. Monjezi et al. (2012) applied TOPSIS method to investigate the blasting operations in the Tajareh limestone mine and select the most appropriate blasting pattern [12]. Similarly, Chu and Su (2012) studied the selection of appropriate fixed seismic shelters for evacuation in an earthquake in cities with the application of TOPSIS [13]. Likewise, Omar and Fayek (2016) applied a TOPSIS-based approach for prioritised aggregation in multi-criteria decision-making problems [14]. Brauers and Zavadskas (2006) applied MOORA method to privatisation in a transition economy [15]. Gadakh (2011) applied the MOORA method for solving multiple criteria (objective) optimisation problem in a milling process [16]. Sinha and Labi (2007) applied MCA methodologies for the evaluation of transportation projects ensuring that the most important costs and impacts were taken into consideration [17]. Behzadian et al. (2010) discussed a comprehensive literature review on methodologies and application of PROMETHEE with 217 scholarly papers applied in environment management, hydrology and water management, business and financial management, chemistry, logistics and transportation, manufacturing and assembly field, energy management, and social and other topics [18]. These and other studies proved that the three multi-criteria methods, namely TOPSIS, MOORA, and PROMETHEE, are applied successfully in several decision-making problems. Nevertheless, the authors found very few applications of these three multi-criteria methods, i.e. TOPSIS, MOORA, and PROMETHEE, in rural road projects’ selection.
2.1. Methodology
This paper extends previous works by Bhandari, Shahi, & Shrestha (2014; 2016) [19, 20] in the multi-criteria evaluation of rural transportation projects in the case of Nepal. This study in the application of multiple criteria analysis methods for the evaluation of rural transportation projects was conducted with the determination of criteria, weighting of criteria, measurement of criteria, scaling of criteria, and aggregation of the performance of criteria with three multi-criteria analysis methods (viz. TOPSIS, MOORA, and PROMETHEE). Four rural roads from the Dang district of Nepal were evaluated. Dang district is an inner Terai district, located at about 280 km west of Kathmandu. Dang covers an area of 2955 km2 with a population of 552,583 inhabitants. The road network in the district is comprised of 807.11 km. Dang district has 24 district roads and 16 village roads. These roads are mainly earthen and gravel type. The local authority has to upgrade these roads to all-weather road standards. Due to the limited budget for the four rural roads of the district road category, that belong to different geographical locations with the characteristics given in Table 1 the interventions have to be prioritized.
| Parameters | Road A | Road B | Road C | Road D |
|---|---|---|---|---|
| Name | Kalakate-Gadawa-Rajapur Road | Bhaisahi-Simaltara-Shantipur | Bijauri-Manpur-Duruwa | PawanNagar-Purandhara |
| Length, km | 15.17 | 16.20 | 9.32 | 9.93 |
| Terrain type | Plain | Plain | Plain | Plain |
| Existing Formation width, m | 5.0 | 3.5 | 4.0 | 4.0 |
| Proposed formation width, m | 6.0 | 6.0 | 6.0 | 6.0 |
| Existing Surface | Gravel | Gravel | Gravel | Gravel |
| Purposed Surface | Ottaseal | Ottaseal | Ottaseal | Ottaseal |
| Population served per km | 1,350 | 988 | 571 | 1,440 |
2.2. Determination of Criteria
Evaluation criteria are important elements for ranking rural road projects, for which there are scarce resources. The evaluation criteria involving 3 aspects of sustainability for ranking rural road projects were determined in this study. The criteria for sustainability assessment depend significantly on the project stakeholders understanding of sustainable development [21]. The evaluation criteria for this study were derived from a thorough literature review, a personnel interview, and an online survey among different experts. A pilot survey was conducted among seven Nepalese experts working in the field of rural roads. This study identified 13 sub-criteria under the headings of the three pillars of sustainability: economic, social, and environmental. The sub-criteria were validated with a wider survey of experts from 24 countries and Nepal through an online questionnaire. The identified criteria and sub-criteria are presented below in Fig. (1).
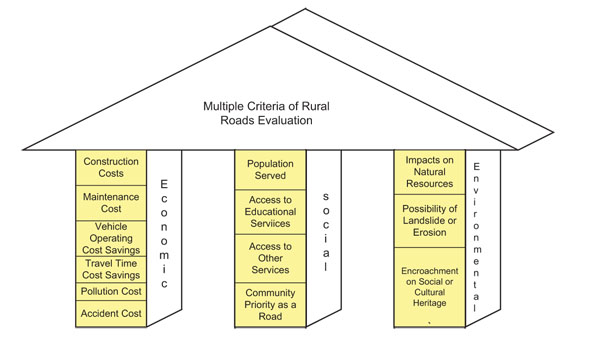
The brief description of the above mentioned sub-criteria and their measure are given below in Table 2.
| Sub-criteria | Brief Description and Measures | ||
|---|---|---|---|
| Road construction costs | The cost of the road from design to delivery [currency per km]. Includes costs of surveying and design, site clearance, earthwork structures, side drains, pavement, establishment of road furniture, land. The costs could be taken from Detailed Project Report. | ||
| Road maintenance costs | The cost of maintaining the road [currency per km per year]. Depends upon the topography of road alignment, precipitation characteristics, road surface, existing structure and drainage system, type of vehicle and loading. Account for both routine and periodic maintenance. The costs could be taken from similar from other roads as per departmental guidelines. | ||
| Vehicle operation costs |
The cost of operating vehicles given the state of the road and the traffic on it [currency per km]. Depends on characteristics of vehicles and roads. Accounts for capital costs including depreciation and interest, fuel consumption, tire consumption, maintenance costs, driver and conductors’ costs oil and Lubricants and overhead costs including garaging and insurance. The Vehicle Operation Costs can be calculated using HDM-VOC model RED-VOC model developed by the World Bank. | ||
| Travel time costs | The total value of time of the passengers who travel on the road [currency/year]. It is obtained as the product of number of travellers, travel time and passengers’ time cost. Different models such as Route Choice Model, Mode Choice Model and Speed Choice Model are used to determine the value of travel time. Due to lack of survey results, appropriate income levels are used in this study. | ||
| Accident costs | The monetary value of the accidents on the road [currency/year]. Obtained as accident cost = traffic volume*risk elasticity*unit cost per accident*external part, taking the risk elasticity from the literature and the external part from insurance policies. The accident costs consist of fatal accidents, non-fatal injury accidents and accident involving property damage only. The predictive models which relate the accident occurrence to traffic volume and a range of attributes such as road design features, traffic control features and site features are used in the estimation of road accident costs [7]. The top-down approach, using the national data on the accident are used in this study. | ||
| Pollution costs | The monetary value of air pollution costs, if possible, lifecycle emissions due to vehicles travelling on the road [currency/year]. This may be obtained considering each pollutant and associating the unit costs of each pollutant’s emission to the total emitted. | ||
| Population served per km | An evaluation of the population that may benefit from the construction of the road [numbers of people/km]. It may be evaluated by using the latest census data and considering the influence area of the road corridor. The latter may be taken as 5 km on both sides of the road, to represent the distance that may be walked within an hour. | ||
| Access to Educational Services |
An evaluation of the number of students in the influence area of the road, using the road services [numbers of students]. The influence area of the road is taken 5 km on both sides of it. | ||
| Access to Other services |
An evaluation of the health services, administrative services and markets served by the road [nos. of institutions]. This criterion may be evaluated by the judgment of the planner during social studies and considering the quantity of health services, administrative services and markets within the influence area of the road, which is taken 5 km on either side of it. |
||
| Road as a community priority | A ranking of the place of the road project as a Community Priority [ranking on a scale of 1-5]. The ranking may be obtained from the judgment of the planners involved in the social studies about the road project. Elements towards the evaluation are the presence of local people in the public meetings, their commitment to the participation in road construction, and the donation of land. |
||
| Impacts on natural systems | An evaluation of the effect of the construction of the road on the natural system [ranking on a scale of 1-9]. This sub-criterion considers elements such as the number trees to be fell down, the area of forest that should be encroached by the road alteration of surface water hydrology of waterways crossed by roads resulting in increased sediment in streams affected by increased soil erosion at construction site. |
||
| Encroachment in historical/ cultural areas and precious ecology (e.g. Sensitive or protected areas) |
An evaluation of the encroachment of an alternative alignment in historical/cultural/ecologically precious areas [ranking on a scale of 1-9]. The indicator measures number and area of encroachment on historical/ cultural areas and precious ecology (e.g. sensitive or protected areas). The ranking may be given by the judgment of the planner. |
||
| Possibility of landslide or flooding | An evaluation of the part of an alignment subject to danger of landslide, erosion or flooding [ranking on a scale of 1-9]. This indicator can be measured by the length of the road passing through landslide/erosion or flooding prone zone, which is then turned into a ranking 1-9 by the planner. | ||
2.3. Determination of Weight
The relative importance or weight of the criteria is a key step in a multiple criteria evaluation. The following methods can be used to establish the weights: a) equal weighting, b) direct weighting, c) regression based observer derived approach, d) the Delphi method [22], e) pairwise comparisons or AHP, and f) Likert scale. The last two methods, AHP and Likert scale, were applied by the first author for the determination of the weights [19, 20] due to the robustness and simplicity of these two methods. The same weights were applied in this study.
The AHP model is based on a basic set of the four axioms [23]. The first axiom states that given any two evaluation elements, stakeholders must be able to provide a pair-wise comparison. The second axiom requires that when comparing any two elements, stakeholders should never decide that one indicator is infinitely superior to another. The third axiom states that the evaluation must be formulated as a hierarchy [23]. In AHP, the criteria are synthesised to a different level of the hierarchy. The overall objective of the decision is at the top level. The criteria used in arriving at this decision are in the lower level. Three major criteria are taken, i.e. costs (economic), social, and environmental aspects in the second level [19]. In the third level economic costs are synthesised into financial and social costs. The financial cost, social costs, social aspects, and environmental aspects have three, three, four, and three sub-criteria respectively. The decision hierarchy for multi-criteria evaluation is given below in Fig. (2).
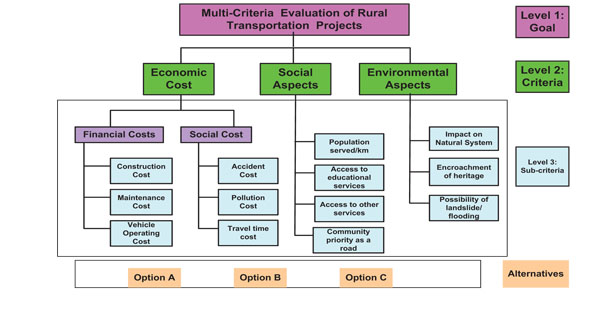
The criteria of each level were compared pairwise in order to determine the relative weights of all criteria & sub-criteria and a pairwise comparison matrix was developed as suggested by Thomas L. Saaty [24]. Saaty suggested an arbitrary rating scale of 1 to 9 based on psychological experiments. The definition of each scale is as follows:
- 1: Two criteria are equally important
- 3: Moderate importance of criterion X over criterion Y
- 5: Strong importance of criterion X over criterion Y
- 7: Very strong importance of criterion X over criterion Y
- 9: Extreme importance of criterion X over Y
2, 4, 6 & 8: Intermediate values between the values mentioned above
With this rating values as elements of matrix aij of the criteria i and j (where aij are the geometric mean values of responses), a pair-wise comparison matrix A has been developed as follows:
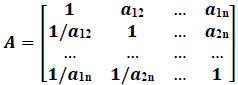 |
(1) |
A Likert Scale is a psychometric scale commonly used in questionnaire surveys. It is simple to construct and easy to be read and filled by the participants. The Likert scale is the sum of responses to several Likert items. A Likert item is simply a statement, which the respondent is asked to evaluate according to any kind of subjective or objective criteria; generally, the level of agreement or disagreement is measured. In this research, an 11-point Likert scale is used to evaluate the weightage of evaluation criteria for rural transportation projects.
The questionnaire for both methods was set up on an online survey tool (Google Forms). Table 3 shows two example questions from the questionnaire in Likert Scale.
| Criteria | Ranking | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0, Not important at all | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10, Extremely Important | |
| Is construction cost an important indicator in the selection of rural roads? | – | – | – | – | – | – | – | – | – | – | – |
| Is maintenance cost an important indicator in the selection of rural roads? | – | – | – | – | – | – | – | – | – | – | – |
2.3.1. Measurement of Criteria
A field survey was conducted for four roads of the Dang district of Nepal to assess the criteria identified in the study. The study collected both quantitative and qualitative data. The data were analysed and the performance measures for each sub-criterion were identified.
2.3.2. Scaling of Criteria
The performance parameters were measured in both quantitative and qualitative terms. The qualitative measurements were converted into quantitative ones in order to obtain the respective commensurate units. The impact of environmental criteria was assessed using the following 5 ratings: very low, low, average, high, and very high, and they were transposed into the following 9-point scale: 9,7,5,3, and 1, respectively.
2.3.3. Multi-Criteria Analysis
Three multi-criteria methods TOPSIS, MOORA, and PROMETHEE are used in this study. In TOPSIS and MOORA methods, excel spreadsheets were used for the calculations. In PROMETHEE method, an academic version of PROMETHEE software was used for the analysis. The software of academic version of the PROMETHEE is available at www.promethee-gaia.net. A brief introduction to these three methods is as follows.
2.4. TOPSIS Method
Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) is “an approach that originates from the geometric concept of the displaced ideal point, according to which a criterion under investigation is seen to be situated in relation to its ideal positive (most favourable) and negative (least favourable) locations” [14]. This method considers three types of attributes or criteria: qualitative benefit attributes/criteria, quantitative benefit criteria, and cost. In this method, two alternatives are hypothesised; i.e. ideal and negative ideal. The ideal alternative has the best level for all attributes considered and the negative alternative has the worst alternative value. TOPSIS selects the alternative, which is the closest to the ideal solution and farthest from negative ideal solution. For the decision making with TOPSIS method, there should be m alternatives and n criteria and a score of each option with respect to each criterion. The following steps are taken with TOPSIS method for decision making [25]:
(i) Step 1: Construct the Normalized Decision Matrix (rij):
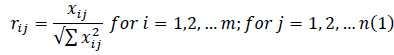 |
(2) |
Where xij = evaluation parameters.
(ii) Step 2: Construct the weighted normalised decision matrix (vij):
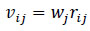 |
(3) |
Where (wj)=weightage of parameters
(iii) Step 3: Determine the ideal and negative ideal solutions:
Ideal solution (A*):
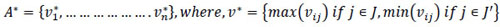 |
(4a) |
Negative ideal solution (A'):
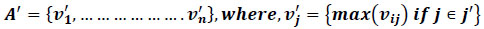 |
(4b) |
(iv) Step 4: Calculate the Separation Measures for each alternative:
The separation from the ideal alternative (S*i) is:
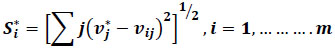 |
(5a) |
Similarly, the Separation Measure from the negative ideal alternative (S'i) is:
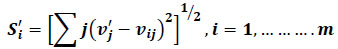 |
(5b) |
(v) Step 5: Calculate the Relative Closeness to the Ideal Solution C*i:
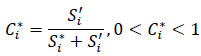 |
(6) |
Select the option with C*i closest to 1.
2.5. MOORA Method
Multi-Objective Optimisation on the basis of Ratio Analysis (MOORA) method was first introduced by Brauers and Zavadskas (2006) [15]. MOORA method is composed of five steps [15, 16, 26-28]:
(i) Step 1: The method starts with a matrix of responses of different alternatives on a different objective (X):
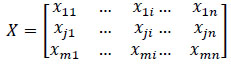 |
(7) |
where, xij x–the response of alternative j on objective or attributes i;
i = 1, 2…. n i=1,2…. n objectives or attributes;
j = 1, 2…. m:j = 1,2……m: the number of alternatives.
(ii) Step 2: The second step is the normalisation of a matrix of responses with the ratio system. Ratio System: In MOORA method each response of an objective is compared to a denominator of representative for all alternatives concerning that objective (x'ij).
 |
(8) |
Thus, normalised responses of the alternatives on the objectives belong to the interval [0,1][0,1].
(iii) Step 3: The third step is an evaluation of positive and negative effects (x'ij). For optimisation, these responses are added in case of maximisation and subtracted in the case of minimisation:
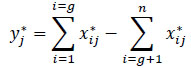 |
(9) |
where: i = 1,2,….gi as the objectives to be maximise di = g + 1, g+ 2,….n as the objectives to be minimised.
(iv) Step 4: In the fourth step, weighted assessment value is determined. In order to give an importance to the criteria, they could be multiplied by the importance factor of the criteria [15].
Finally, all alternatives are ranked, according to the obtained ratios (i.e. decreasing value of y*j).
2.5. PROMETHEE Method
Preference Ranking Organisation Method for Enrichment Evaluations (PROMETHEE) belongs to the family of outranking methods as it was initiated by B. Roy at the end of the ‘60 with the ELECTRE methods [29]. The original PROMETHEE methods were conceived by J. P. Brans in 1982 and were further extended by Vincke and Brans in 1985 [18]. The PROMETHEE methods include several unique tools for this purpose, such as the weight stability intervals and the Walking Weights interactive procedure. In 1989, the introduction of Geometrical Analysis for Interactive Aid (GAIA) added a descriptive complement to the PROMETHEE rankings. A graphical representation of the multi-criteria problem enables the decision maker to better understand the available choices and the necessary compromises he or she will have to make to achieve the best decision. GAIA can also be used to see the impact of the criteria weights on the PROMETHEE rankings. “The evaluation table is the starting point of the PROMETHEE method. In this table, the alternatives are evaluated on different criteria. These evaluations involve essentially numerical data” [30]. There are several types of PROMETHEE (viz. PROMETHEE-I, PROMETHEE-II, PROMETHEE-III, PROMETHEE-IV, PROMETHEE-TRI, PROMETHEE CLUSTER, etc.). The most common used methodology is PROMETHEE-II, which is used in complete ranking. “It is interactive and is able to classify and order alternatives which are complex and difficult to compare. In addition, it has other characteristics such as: simplicity, clarity and stability” [31]. The basic principle of PROMETHEE II is based on a pair-wise comparison of alternatives along each recognised criterion. Alternatives are evaluated according to different criteria, which have to be maximised or minimised.
The implementation of PROMETHEE-II requires two additional types of information, namely: information on the relative importance (i.e. the weights) of the criteria considered and information on the decision maker’s preference function, which he/she uses when comparing the contribution of the alternatives in terms of each separate criterion. The weights and the preference function determine the preference structure of the decision-maker. PROMETHEE does not provide specific guidelines for determining these weights but assumes that the decision-maker is able to weigh the criteria appropriately, at least when the number of criteria is not too large. The preference function (Pj) translates the differences between the evaluations (i.e. scores) obtained by two alternatives (a and b) in terms of a particular criterion, into a preference degree ranging from 0 to 1. The procedure for implementing PROMETHEE-II “is started to determine deviations based on the pairwise comparison. It is followed by using the relevant preference function for each criterion in Step 2, calculating [the] global preference index in Step 3, and calculating positive and negative outranking flows [strength & weakness] for each alternative and partial ranking in Step 4” [18]. Finally, the procedure ends in Step 5 with the calculation of net outranking flow for each alternative and complete ranking.
3. RESULTS AND ANALYSIS
As mentioned previously, the study was conducted for four rural roads in Dang district of Nepal. The detailed identification of criteria, weights, and performance parameters were described in previous articles [19, 20]. There were various MCA methods applied in the transportation projects [10, 32] earlier but in this paper three MCA methods (PROMETHEE, TOPSIS and MOORA) are applied and compared. The values and weights of the criteria are presented below in Table 42.
2 Another approach would be to calculate the Cost/Benefit (C/B) ratio or else the Economic Internal rate of Return (EIRR) for the economic pillar combining the first six parameters into a single indicator. Moreover, an even better approach could be using the indicator Net Present Value (NPV)/Construction Cost, which normalizes the net benefits in relation to cost. Since the parameters 11, 12 and 13 have the same ordinal scale (1-9) and they refer to the environmental pillar, these could be combined into a composite index. The measurement of parameters 7, 8 and 9 are explained in Table 1. Moreover, for the parameters 7, 8 and 9, the same discrete 5-point scale that was used for the parameter 10 could be used too. With such an approach, the array of factors could be streamlined and hence possible double-counting of benefits would be avoided, however, the above-mentioned 13 indicators are used in this way in this study to make the different aspects of rural roads more understandable to the decision makers.
| Sr. No. | Parameters | Road A | Road B | Road C | Road D | Weights (AHP) | Weights (Likert scale) |
|---|---|---|---|---|---|---|---|
| 1 | Construction cost (103,USD) | 1327.92 | 1234.52 | 758.73 | 748.39 | 6.70% | 6.8% |
| 2 | Maintenance cost (103,USD/year) | 110.45 | 117.96 | 67.86 | 72.31 | 9.41% | 7.5% |
| 3 | Vehicle operation cost saving (103, USD/year) | 33.23 | 76.17 | 25.44 | 69.09 | 5.04% | 6.3% |
| 4 | Travel time saving cost (103, USD) | 3.43 | 8.83 | 2.85 | 9.85 | 4.79% | 6.8% |
| 5 | Accidents cost (103, USD) | 0.00 | 0.00 | 0.00 | 0.00 | 8.29% | 7.9% |
| 6 | Pollution cost (103, USD) | 32.20 | 65.98 | 49.87 | 93.86 | 3.96% | 5.9% |
| 7 | Population served per km | 1,350 | 988 | 571 | 1,440 | 10.96% | 8.9% |
| 8 | Access to educational services (No. of students) | 2,517 | 4,400 | 1,975 | 475 | 6.53% | 8.0% |
| 9 | Access to other services (No.) | 3 | 3 | 1 | 1 | 8.87% | 8.8% |
| 10 | Road as a community priority (5-point scale) | 5 | 5 | 5 | 5 | 7.69% | 8.2% |
| 11 | Encroachment on historical areas (9-point scale i.e. 1 to 9) | 9 (very low) | 9 (very low) | 9 (very low) | 9 (very low) | 8.46% | 8.4% |
| 12 | Possibility of landslide or flooding (9-point scale i.e. 1 to 9) | 9 (very low) | 9 (very low) | 9 (very low) | 9 (very low) | 7.79% | 7.9% |
| 13 | Impacts on natural systems (9-point scale i.e. 1 to 9) | 1 (very high) | 7 (low) | 9 (very low) | 3 (high) | 11.54% | 8.5% |
3.1. Ranking with TOPSIS Method
The strength of TOPSIS is that it is easy to implement having an understandable principle, it is applicable when exact and total information is collected, it considers both the positive and negative ideal solutions, and it provides a well-structured analytical framework for alternatives ranking [7]. The ranking of the abovementioned roads with TOPSIS is described below.
- Step 1: The decision-making was formulated with the evaluation parameter xij as given above in Table 4.
- Step 2: The Normalised Matrix rij of the four roads is presented below in Table 5.
| Criteria | Road A | Road B | Road C | Road D |
|---|---|---|---|---|
| 1 | 0.631 | 0.587 | 0.361 | 0.356 |
| 2 | 0.583 | 0.622 | 0.358 | 0.381 |
| 3 | 0.299 | 0.686 | 0.229 | 0.622 |
| 4 | 0.245 | 0.633 | 0.204 | 0.706 |
| 5 | 0.249 | 0.511 | 0.386 | 0.727 |
| 6 | 0.224 | 0.717 | 0.189 | 0.632 |
| 7 | 0.592 | 0.433 | 0.250 | 0.632 |
| 8 | 0.461 | 0.806 | 0.362 | 0.087 |
| 9 | 0.671 | 0.671 | 0.224 | 0.224 |
| 10 | 0.500 | 0.500 | 0.500 | 0.500 |
| 11 | 0.000 | 0.000 | 0.000 | 0.000 |
| 12 | 0.000 | 0.000 | 0.000 | 0.000 |
| 13 | 0.085 | 0.592 | 0.761 | 0.254 |
(iii) Step 3: The Weighted Normalised Matrix is calculated by the multiplication of the Normalised Matrix [rij] with the weights of the respective criteria in AHP as specified in Table 4. The results with AHP are presented below in Table 6.
| Criteria | Road A | Road B | Road C | Road D |
|---|---|---|---|---|
| 1 | 4.230 | 3.933 | 2.417 | 2.384 |
| 2 | 5.482 | 5.855 | 3.368 | 3.589 |
| 3 | 1.509 | 3.458 | 1.155 | 3.136 |
| 4 | 1.175 | 3.030 | 0.979 | 3.380 |
| 5 | 2.067 | 4.234 | 3.201 | 6.023 |
| 6 | 0.888 | 2.839 | 0.748 | 2.505 |
| 7 | 6.490 | 4.749 | 2.745 | 6.922 |
| 8 | 3.010 | 5.261 | 2.362 | 0.568 |
| 9 | 5.950 | 5.950 | 1.983 | 1.983 |
| 10 | 3.845 | 3.845 | 3.845 | 3.845 |
| 11 | 0.000 | 0.000 | 0.000 | 0.000 |
| 12 | 0.000 | 0.000 | 0.000 | 0.000 |
| 13 | 0.975 | 6.827 | 8.778 | 2.926 |
(iv) Step 4: The Ideal Solution and the Negative Ideal Solution of the Weighted Normalised Matrix are presented below in Table 7.
| Criteria | Ideal Solution | Negative Ideal Solution |
|---|---|---|
| 1 | 2.384 | 4.230 |
| 2 | 3.368 | 5.855 |
| 3 | 3.458 | 1.155 |
| 4 | 3.380 | 0.979 |
| 5 | 2.067 | 6.023 |
| 6 | 0.748 | 2.839 |
| 7 | 6.922 | 2.745 |
| 8 | 5.261 | 0.568 |
| 9 | 5.950 | 1.983 |
| 10 | 3.845 | 3.845 |
| 11 | 0.000 | 0.000 |
| 12 | 0.000 | 0.000 |
| 13 | 8.778 | 0.975 |
(v) Step 5: The separation measures from the ideal solution and the negative ideal solution of each road are presented below in Table 8.
| Separation Measure | Road A | Road B | Road C | Road D |
|---|---|---|---|---|
| Ideal solution (S*i) | 10.046 | 9.908 | 9.819 | 15.172 |
| Negative ideal solution S'i | 7.535 | 9.665 | 9.318 | 6.692 |
(vi) Step 6: The Relative Closeness and their ranking order of the rural transportation projects are presented below in Table 9. The ranking of the rural road projects is as per the decreasing order of the Relative Closeness of the respective roads.
| Description | Road A | Road B | Road C | Road D |
|---|---|---|---|---|
| Relative Closeness | 0.429 | 0.494 | 0.487 | 0.306 |
| Ranking | 3 | 1 | 2 | 4 |
3.2. Ranking with Multi-Objective Optimisation on the Basis of Ratio Analysis (MOORA) Method
The same Decision Matrix with the TOPSIS is used as presented in Table 4. Then, the Ratio Matrix is derived as presented in Table 10. Similarly, the Normalised Matrix is presented in Table 11.
| Criteria | Road A | Road B | Road C | Road D | Max/Min |
|---|---|---|---|---|---|
| 1 | 0.6314 | 0.5870 | 0.3608 | 0.3558 | minimize |
| 2 | 0.5825 | 0.6222 | 0.3579 | 0.3814 | minimize |
| 3 | 0.2993 | 0.6861 | 0.2291 | 0.6223 | maximize |
| 4 | 0.2454 | 0.6326 | 0.2044 | 0.7056 | maximize |
| 5 | 0.2493 | 0.5108 | 0.3861 | 0.7266 | minimize |
| 6 | 0.2243 | 0.7169 | 0.1889 | 0.6325 | minimize |
| 7 | 0.5921 | 0.4333 | 0.2504 | 0.6316 | maximize |
| 8 | 0.4609 | 0.8057 | 0.3617 | 0.0870 | maximize |
| 9 | 0.6708 | 0.6708 | 0.2236 | 0.2236 | maximize |
| 10 | 0.5000 | 0.5000 | 0.5000 | 0.5000 | maximize |
| 11 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | maximize |
| 12 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | maximize |
| 13 | 0.0845 | 0.5916 | 0.7606 | 0.2535 | maximize |
| Criteria | Road A | Road B | Road C | Road D |
|---|---|---|---|---|
| 1 | -4.2304 | -3.9328 | -2.4171 | -2.3842 |
| 2 | -5.4816 | -5.8545 | -3.3682 | -3.5889 |
| 3 | 1.5086 | 3.4579 | 1.1547 | 3.1362 |
| 4 | 1.1754 | 3.0301 | 0.9790 | 3.3797 |
| 5 | -2.0666 | -4.2341 | -3.2005 | -6.0235 |
| 6 | -0.8884 | -2.8391 | -0.7479 | -2.5045 |
| 7 | 6.4895 | 4.7494 | 2.7448 | 6.9222 |
| 8 | 3.0098 | 5.2614 | 2.3616 | 0.5680 |
| 9 | 5.9502 | 5.9502 | 1.9834 | 1.9834 |
| 10 | 3.8450 | 3.8450 | 3.8450 | 3.8450 |
| 11 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 12 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 13 | 0.9753 | 6.8272 | 8.7778 | 2.9259 |
Finally, the ranks are determined based on the Reference Point and the Deviation from the Reference Point as presented in Table 12.
| Criteria | Reference Point | Deviation from Reference Point | |||
|---|---|---|---|---|---|
| Road A | Road B | Road C | Road D | ||
| 1 | -2.3842 | -1.8462 | -1.5487 | -0.0329 | 0.0000 |
| 2 | -3.3682 | -2.1134 | -2.4864 | 0.0000 | -0.2207 |
| 3 | 3.4579 | -1.9493 | 0.0000 | -2.3032 | -0.3217 |
| 4 | 3.3797 | -2.2043 | -0.3496 | -2.4008 | 0.0000 |
| 5 | -2.0666 | 0.0000 | -2.1675 | -1.1339 | -3.9569 |
| 6 | -0.7479 | -0.1405 | -2.0912 | 0.0000 | -1.7566 |
| 7 | 6.9222 | -0.4326 | -2.1728 | -4.1773 | 0.0000 |
| 8 | 5.2614 | -2.2516 | 0.0000 | -2.8997 | -4.6934 |
| 9 | 5.9502 | 0.0000 | 0.0000 | -3.9668 | -3.9668 |
| 10 | 3.8450 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 11 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 12 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 13 | 8.7778 | -7.8025 | -1.9506 | 0.0000 | -5.8518 |
| Total Deviation from Reference Point | -18.7405 | -12.7668 | -16.9147 | -20.7680 | |
| Ranking | 3 | 1 | 2 | 4 | |
3.3. Ranking with PROMETHEE Method
The ranking of the above-mentioned roads was also studied with the application of the VISUAL PROMETHEE MCDA decision aid software. The academic version of this software was used in this case study. The software was downloaded from the following link http://www.promethee-gaia.net. The same input of impact matrix and the weights derived with AHP presented in Table 4 were used in this study. All criteria were defined by a linear preference function. The statistics of the data of the rural road projects are presented in Table 13. The preference parameters and rankings with PROMETHEE are presented in Tables 14 and 15, respectively. The Range of Stability derived from Visual Stability Interval at Stability Level four is presented in Table 16. The results are presented in Figs. (3-7).
| Criteria | Minimum | Maximum | Average | Standard Deviation |
|---|---|---|---|---|
| 1 | 77,048 | 136,776 | 10,3282.3 | 26,273.65 |
| 2 | 6,990 | 12,150 | 9,491 | 2,294.14 |
| 3 | 2,620 | 7,846 | 5,251.25 | 2,262.52 |
| 4 | 294 | 1,015 | 643 | 322.33 |
| 5 | 3,317 | 9,668 | 6,229.5 | 2,335.62 |
| 6 | 22,704 | 86,188 | 52,973.25 | 28,404.56 |
| 7 | 571 | 1,440 | 1,087 | 343 |
| 8 | 475 | 4,400 | 2,342 | 1,404 |
| 9 | 1 | 3 | 2 | 1 |
| 10 | 5 | 5 | 5 | 0 |
| 11 | 9 | 9 | 9 | 0 |
| 12 | 9 | 9 | 9 | 0 |
| 13 | 1 | 9 | 5 | 3 |
| Criteria | Min/Max | Weight | Preference Fn. | Thresholds | Q: Indifference | P: Preference |
|---|---|---|---|---|---|---|
| 1 | min | 6.70 | Linear | Absolute | 1,000 | 137,000 |
| 2 | 9.41 | 20 | 12,200 | |||
| 3 | max | 5.04 | 10 | 7,850 | ||
| 4 | 4.79 | 100 | 1,020 | |||
| 5 | min | 8.29 | 100 | 9,700 | ||
| 6 | 3.96 | 100 | 86,200 | |||
| 7 | max | 10.96 | 25 | 1,440 | ||
| 8 | 6.53 | 25 | 4,400 | |||
| 9 | 8.87 | 1 | 3 | |||
| 10 | 7.69 | 1 | 5 | |||
| 11 | 8.46 | 1 | 9 | |||
| 12 | 7.79 | 1 | 9 | |||
| 13 | 11.54 | 1 | 9 |
| Road | Phi | Phi+ | Phi- | Ranking |
|---|---|---|---|---|
| Road A | -0.0287 | 0.1232 | 0.1519 | 3 |
| Road B | 0.0678 | 0.1681 | 0.1003 | 1 |
| Road C | 0.0049 | 0.1475 | 0.1426 | 2 |
| Road D | -0.0440 | 0.1178 | 0.1618 | 4 |
| Sr. No. | Criteria | Lower Bound | Upper Bound |
|---|---|---|---|
| 1 | Construction cost (103, US dollar) | 0.80 | 9.14 |
| 2 | Maintenance cost (103, US dollar/year) | 2.55 | 12.54 |
| 3 | Vehicle operation cost saving (103, US dollar/year) | 0.00 | 7.31 |
| 4 | Travel time saving cost (103, US dollar) | 0.00 | 6.58 |
| 5 | Accidents cost (103, US dollar) | 6.62 | 19.32 |
| 6 | Pollution cost (103, US dollars) | 1.98 | 9.74 |
| 7 | Population served per km (Nos.) | 0.00 | 14.98 |
| 8 | Access to educational services (Nos. of students) | 4.13 | 22.64 |
| 9 | Access to other services (Nos.) | 6.72 | 13.24 |
| 10 | Road as a community priority (5-point scale) | 0.00 | 100.00 |
| 11 | Encroachment on historical areas (9-point scale) | 0.00 | 100.00 |
| 12 | Possibility of landslide or flooding (9-point scale) | 0.00 | 100.00 |
| 13 | Impacts on natural systems (9-point scale) | 8.70 | 16.65 |
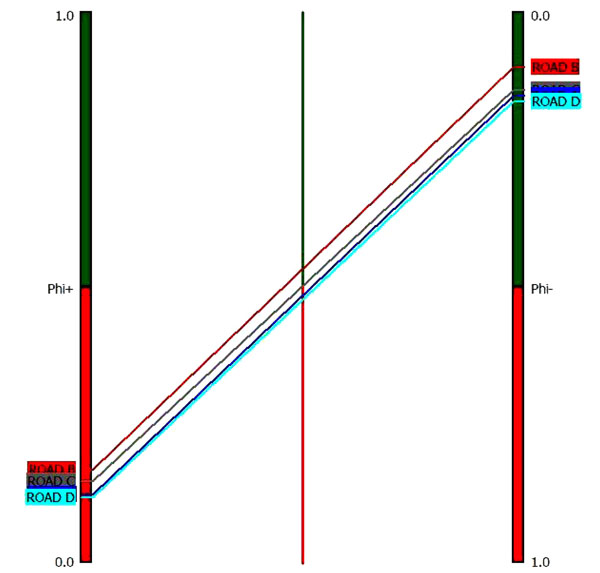
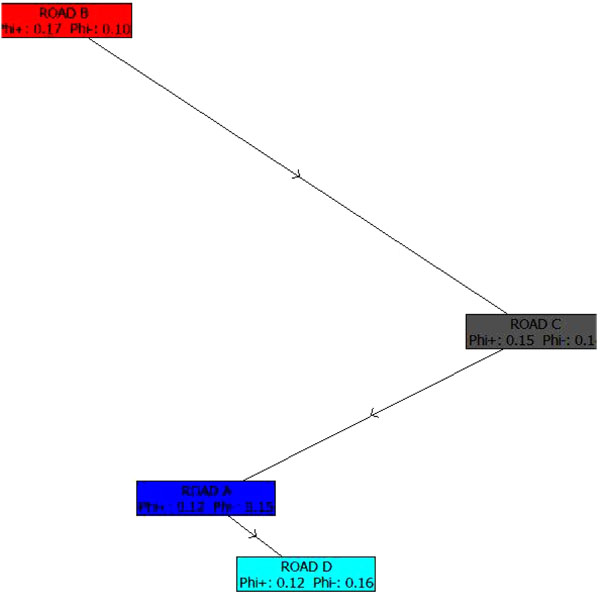
In Fig. (3) the partial ranking of the analysis with PROMETHEE-I is presented. It can be noticed that the Road B is the highest and the Road C is the second highest preferred to all the other roads and that Road D is the lowest preferred to all the others road projects in PROMETHEE-I partial ranking. No projects are identified as incomparable (i.e. worse phi- and best phi+ or reverse while comparing between two projects).
In Fig. (4) the PROMETHEE-II complete ranking shows that Road B has the highest phi. Road C has the second highest phi. Road A and Road D have almost similar net phi. Road D has the lowest net phi value. In Fig. (5) the PROMETHEE Diamond shows that Road B (in red colour) overlaps all the other roads. Obviously, this project is preferred to all the other projects according to the PROMETHEE-II partial ranking.
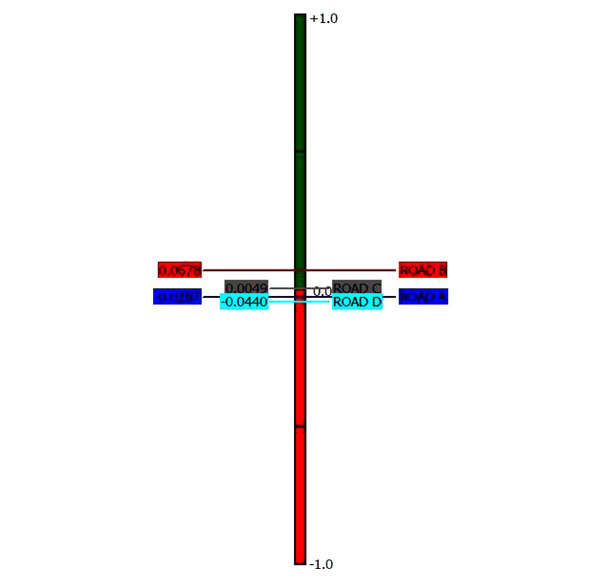
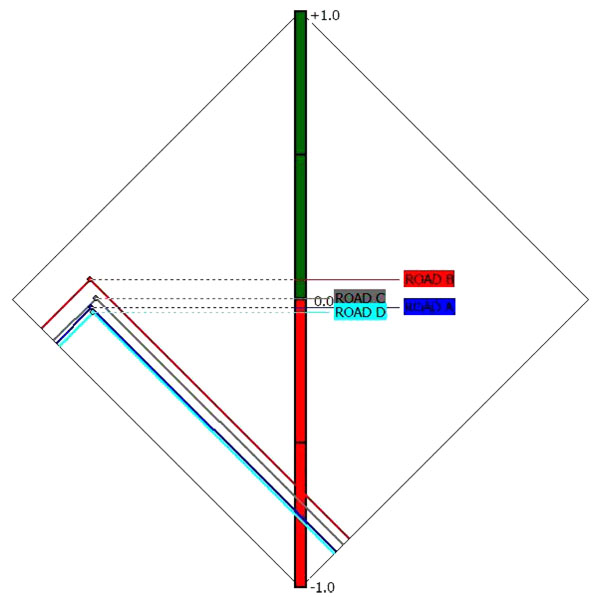
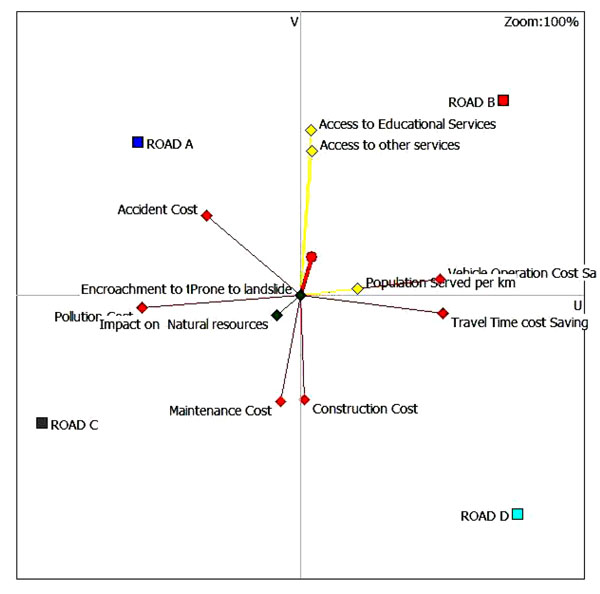
Fig. (6) represents the GAIA Plane obtained principle component analysis to the alternative of the problem. At first, it may be noticed that the alternative Road C performs well on the environmental, maintenance cost, and pollution cost criteria. It is neutral in travel time saving cost and accident cost criteria and it has a poor performance on the population served per km, vehicle operation cost saving, access to educational services, and access to other services criteria. On the other hand, Road B performs well on access to educational services, access to other services, population served per km, and vehicle operation cost saving criteria. It is neutral in the travel time savings cost, construction cost, and accident cost criteria and it has a poor performance on maintenance cost and impact on natural resources criteria. On the contrary, Road D performs well on the construction cost and travel time saving cost criteria. It is neutral in access to educational services, access to other services, population served per km, vehicle operation cost saving, impact on natural resources, and pollution cost criteria and has a poor performance on accident cost criterion. Similarly, Road A performs well on accident cost criterion. It is neutral in vehicle operation cost saving, population served per km, pollution cost, impact on natural resources, and maintenance cost criteria and it has a poor performance on travel time saving cost and construction cost criteria. Thus, the use of complementary tools such as the GAIA Plane, Diamond, etc. provides support to the decision maker in order to understand the result and make the best selection for the final solution.
In Fig. (7) the positive and negative outranking flows show that Road B is preferred compared to all the other roads. Road C and Road A follow. Road D is the least preferred alternative. No road projects are incomparable.
3.3.1. Ranking with the Weights of Likert Scale
The study was also conducted using the weights of Likert scale presented in Table 4. The summary of rankings with weights of the Likert scale and the multi-criteria methods TOPSIS, MOORA, and PROMETHEE are presented below in Tables 17-19 respectively.
| Description | Road A | Road B | Road C | Road D |
|---|---|---|---|---|
| Relative Closeness | 0.471 | 0.540 | 0.454 | 0.373 |
| Ranking | 2 | 1 | 3 | 4 |
| Criteria | Reference Point | Deviation from Reference Point | |||
|---|---|---|---|---|---|
| Road A | Road B | Road C | Road D | ||
| 1 | -2.4197 | -1.8738 | -1.5718 | -0.0334 | 0.0000 |
| 2 | -2.6845 | -1.6844 | -1.9817 | 0.0000 | -0.1759 |
| 3 | 4.3224 | -2.4366 | 0.0000 | -2.8790 | -0.4022 |
| 4 | 4.7980 | -3.1293 | -0.4963 | -3.4082 | 0.0000 |
| 5 | -1.9694 | 0.0000 | -2.0656 | -1.0806 | -3.7707 |
| 6 | -1.1143 | -0.2094 | -3.1157 | 0.0000 | -2.6172 |
| 7 | 5.6211 | -0.3513 | -1.7644 | -3.3922 | 0.0000 |
| 8 | 6.4458 | -2.7585 | 0.0000 | -3.5525 | -5.7500 |
| 9 | 5.9032 | 0.0000 | 0.0000 | -3.9355 | -3.9355 |
| 10 | 4.1000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 11 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 12 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 13 | 6.4654 | -5.7470 | -1.4368 | 0.0000 | -4.3103 |
| Total Deviation from Reference Point | -18.1904 | -12.4323 | -18.2814 | -20.9617 | |
| Ranking | 2 | 1 | 3 | 4 | |
| Road | Phi | Phi+ | Phi- | Ranking |
|---|---|---|---|---|
| Road A | -0.0112 | 0.1310 | 0.1422 | 3 |
| Road B | 0.0702 | 0.1743 | 0.1041 | 1 |
| Road C | -0.0057 | 0.1404 | 0.1461 | 2 |
| Road D | -0.0533 | 0.1162 | 0.1695 | 4 |
4. DISCUSSION
In this research, three MCA evaluation methods (viz. TOPSIS, MOORA, and PROMETHEE) were used to evaluate four rural transportation projects (viz. Road A, Road B, Road C, and Road D). The summary of the study is presented below in Table 20.
| Name of the road | TOPSIS | MOORA | PROMETHEE | |||
|---|---|---|---|---|---|---|
| AHP | Likert | AHP | Likert | AHP | Likert | |
| Road A | III | II | III | II | III | III |
| Road B | I | I | I | I | I | I |
| Road C | II | III | II | III | II | II |
| Road D | IV | IV | IV | IV | IV | IV |
The results of this study showed that in the MCA methods TOPSIS, MOORA, and PROMETHEE the same rankings of the rural road projects Road B, Road D were found for both AHP and Likert scale weights. The rankings of Road A and Road C were found different for AHP and Likert weights in TOPSIS and MOORA methods. In the case of Road B and Road D, the values of relative closeness are 0.540 and 0.373 and deviation from the reference point -12.4323 and -20.9617, respectively. On the other hand, the values of the relative closeness and deviation from the reference point of Road A and Road C are 0.4710 and 0.4540, and -18.1904 and -18.2814, respectively. The absolute values of difference of the relative closeness and deviation from the reference point of the rural roads Road B and Road D are 0.168 and 8.5295 respectively, and for the rural roads Road A and Road C are 0.069 and 0.910 respectively. This shows that if the difference between relative closeness and/or deviation from the reference point is more, the ranking does not change for some deviation of the weights. Thus, the measurements of the weights with robust unbiased methods (e.g. AHP) and the measurement of the criteria with accurate values is an important issue for the application of different multi-criteria analysis methods.
Obviously, all the three methods used are quite capable of dealing both with quantitative and qualitative data. In the multi-criteria evaluation, it is possible that different stakeholders may participate to determine the weights of different criteria. Input of experts to find the value of the economic dimension is also needed. All the three dimensions of sustainability are included. Moreover, the inclusion of the environmental dimension helps to sensitise the stakeholders about the importance of the protection of the environment.
The TOPSIS and MOORA methods are very simple and can be applied without any software. The outranking methods, like PROMETHEE, are useful to make a decision on the application of different criteria and also in an alternative scenario with the application of the software. A different analysis of PROMETHEE (e.g. partial ranking, complete ranking, PROMETHEE Diamond, GAIA Plane, and positive and negative outranking flow) give a clear picture on the ranking of the alternatives (rural roads in the case of this study). The range of stability of weights can be identified easily in PROMETHEE with the application of the software. The results of multi-criteria methods depend upon the value of performance measures, weights, normalisation, and aggregation procedures. The MCA methods used (e.g. TOPSIS, MOORA, and PROMETHEE), in which weights are derived using robust methods (e.g. AHP) and precise measurement of the criteria of rural roads, generally return the same rankings.
This study proved that the developed model with the 13 parameters was useful for the evaluation of rural roads in the context of Nepal, since all the three multi-criteria analysis methods applied returned similar ranking results.
CONCLUSION
In this paper, a comparison of the application of three multi-criteria methods (viz. TOPSIS, MOORA, and PROMETHEE) took place. The criteria and weights derived in previous studies on rural roads were applied in this study. Performance measurements of four rural roads of a district of Nepal were used for the analysis. Sensitivity analysis of weights was also done with PROMETHEE method. The results of the three multi-criteria methods returned the same rankings for Road B and Road D but deviations in ranking for Road A and Road C were observed. The multi-criteria analysis methods used (e.g. TOPSIS, MOORA, and PROMETHEE), in which weights are derived using robust methods (e.g. AHP) and precise measurement of the criteria of rural roads, generally return the same rankings. This study proved the successful application of these three MCA methods with the inclusion of the three pillars of sustainability (viz. economic, social, and environmental dimension). Therefore, the same model seems to be promising for other applications on rural road projects both in Nepal and in other developing countries.
LIST OF ABBREVIATIONS
| AHP | = Analytic Hierarchy Process |
| B/C | = Benefit Cost Ratio |
| CBA Cost | = Benefit Analysis |
| DM | = Decision-Making |
| EIRR | = Economic Internal Rate of Return |
| ELECTRE | = ELimination Et Choix Traduisant la REalité (Elimination and Choice Expressing Reality) |
| GAIA | = Geometrical Analysis for Interactive Aid |
| GIS | = Geographic Information System |
| MAUT/MAVT | = Multi-Attribute Utility Theory / Multi-Attribute Value Theory |
| MCA | = Multi-Criteria Analysis |
| MCDM | = Multiple-Criteria Decision-Making |
| MOORA | = Multi-Objective Optimisation on the basis of Ratio Analysis |
| NPV | = Net Present Value |
| NR | = Nepalese Rupees |
| PROMETHEE | = Preference Ranking Organization METHod for Enrichment of Evaluations |
| SMART | = Simple Multi-Attribute Rating Technique |
| TOPSIS | = Technique for Order of Preference by Similarity to Ideal Solution |
| USD | = United States of America Dollar |
| VIKOR | = VIšekriterijumsko KOmpromisno Rangiranje |
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
Erasmus+ International Programme funded a scholarship for the first author for the exchange program at the Aristotle University of Thessaloniki, Greece. There are no conflicts of interest.
ACKNOWLEDGEMENTS
This paper is based on the doctoral dissertation of the first author at the Institute of Engineering, Tribhuvan University, Nepal. This article was written during his period of study at the Aristotle University of Thessaloniki, Greece. The first author would like to thank the Erasmus+ International Programme for providing a scholarship for the exchange program at the Aristotle University of Thessaloniki, Greece.


