All published articles of this journal are available on ScienceDirect.
Degradation Prediction of Rail Tracks: A Review of the Existing Literature
Abstract
In the past few decades, the railway infrastructure has been widely expanded in urban and rural areas, making it the most complex matrix of rail transport networks. Safe and comfortable travel on railways has always been a common goal for transportation engineers and researchers, and requires railways in excellent condition and well-organized maintenance practices. Degradation of rail tracks is a main concern for railway organizations as it affects the railway’s behaviour and its parameters, such as track geometry, speed, traffic and loads. Therefore, the prediction of the degradation of rail tracks is very important in order to optimise maintenance needs, reduce maintenance and operational costs of railways, and improve rail track conditions.
This paper provides a comprehensive review of rail degradation prediction models, their parameters, and the strengths and weaknesses of each model. A comprehensive discussion of existing research and a comparison of different models of degradation of rail tracks is also provided. Finally, this review presents concluding remarks on the limitations of existing studies and provides recommendations for further research and appraisal practices.
1. INTRODUCTION
Public transport consists of extensive networks and a wide variety of transport services. As a strategy to tackle the growing demand for transport service providers in the past tried expanding the existing networks and kept expanding them till they meet those demands. However, this has become an option, which is not viable due to lack of land space and economical restrictions. Instead of that they have focused on intelligently managing and maintaining their current networks to the optimum levels. They have also focused on maintenance planning, which covers a wide range of transport engineering asset-management systems, optimisation planning and maintenance decision-making. One of the main recent concerns in rail public transport is the degradation of rail tracks. Although the degradation of rail tracks is generally slow, it may lead to high-risk failures with enormous financial maintenance costs. Therefore, the prediction of rail track degradation is a very important process in order to optimise maintenance needs, reduce costs, and improves track conditions (i.e. the quality of materials) in relation to different degradation components, such as track load, time, speed of vehicles and other parameters.
This study reviews the existing literature on the prediction of degradation of rail tracks. The emphasis is on studies published in relationship to recent degradation activities of rail tracks on light rail (i.e. tram) and heavy rail (i.e. train) routes. The main focus is of this review is to understand the behaviour of each predicted degradation model, taking into account the variables and factors. It is hoped that this study will improve the prediction of degradation modelling to optimise maintenance practices and minimise track imperfections.
This paper is structured as follows. Section 2 presents an overview of railway track structure and track degradation modelling, highlighting the contributing factors. It also includes a classification scheme for rail degradation models, and discusses in detail the development of each degradation model and its variables. Section 3 summarises the main findings of the literature review, including a discussion of the limitations of existing studies. Section 4 provides some concluding remarks and recommendations for future research.
2. REVIEW OF RAIL TRACK DEGRADATION MODELS
The core of this paper is the review of rail track degradation models in the literature. To understand the dynamic behaviour of degradation, it is first important to provide an overview of the railway track structure and factors affecting track degradation modelling. This section of the literature review briefly introduces the structure of railways, followed by an outline of rail degradation modelling and associated factors.
2.1. Overview of Railway Track Structure
A railway is a track where the vehicle moves along two parallel rails. These rails support the wheels of the vehicles including the locomotives and wagons. The structure of a railway is divided into two sections:
- Superstructure (top rail track),
- Substructure (below the rail track).
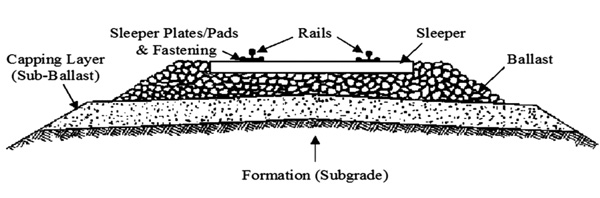
The superstructure consists of the rails, the fastening system, rail pads and sleepers, whereas the substructure consists of the ballast, sub-ballast and the subgrade [1].
Traditional ballasted tracks and concrete slab tracks (ballast-less track) are the most common types of rail tracks [2]. On traditional ballasted tracks, the rails are set on wooden or concrete sleepers. The sleepers lie on a sheet of ballast that distributes the loading to the subgrade. Top ballast is situated between the sleepers and on the shoulders to retain longitudinal and lateral stability [3]. Ballast cleaning and renewal is also part of the maintenance routine. Basically, cleaning the ballast is achieved by a specific cleaning machine. It is required when the ballast becomes so fouled that it cannot fulfil its functions. If cleaning does not succeed, renewal is required and the ballast is completely replaced. Fig. (1) shows the structural components of a typical railway track.
2.2. Track Degradation Modelling
Rail degradation is a failure process, which leads to a rail defect (fault). Various studies on rail degradation have been performed by a number of researchers over the years [4-8]. There is a need to reduce rail degradation and predict rail failure in order to develop an effective rail maintenance strategy. A number of factors contribute to the degradation of rail tracks, including the condition of assets (i.e. sleepers, fastenings and ballast) [9], age of rails and axle load [2, 10], speed [10], traffic density [11, 12], traffic type, rail-wheel interaction [10], Million Gross Tonnes (MGTs) [2], track curvature [3, 10], rail size, rail profile, and rail track construction [2], rail track elevation, rail track super-elevation and rail welding [10], and rail lubrication [13].
2.3. A Classification Scheme of Rail Degradation Models
In degradation modelling, the condition of rail tracks is predicted at some future point when maintenance may need to be implemented. Different degradation models have been developed by previous researchers [14 ,15-20] based on the influencing factors and different characteristics of railroad tracks, such as rail type, size, and profile.
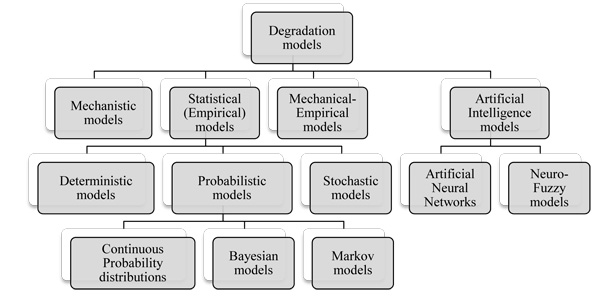
Accordingly, rail degradation models can be classified into four general approaches, as shown in Fig. (2) below.
2.3.1. Mechanistic Models
The mechanistic approach involves establishing, by theory or testing, the mechanical properties of rail track structure. It includes the calculation of forces and stresses in order to assess the degradation variation of the rail [4].
Different studies have been applied using the mechanistic approach to predict the degradation of rail tracks. These studies can be categorized into two main categories as follows:
- Models based on Japanese studies [21-24]
- Models based on Austrian studies analysing the development of track quality from a passenger’s point of view [3, 24, 25].
Japanese railway companies established the relationship of the settlement of railway ballast and cyclic loading (train speed) [23]. The following typical equation is frequently used to measure the track deformation (y) of heavy-haul narrow gauge and high standard gauge tracks:
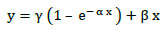 |
(1) |
Where, x represents the repeated number of loadings or tonnage carried by the track, α is the vertical acceleration required to initiate slip which can be measured using spring-loaded plates of the ballast material on a vibrating table, β is a coefficient proportional to the sleeper pressure and peak acceleration experienced by the ballast characteristics and the presence of water, and γ is a constant dependent on the initial packing of the ballast material.
Sato (1995) found that traffic, time, track condition and humidity are the variables which have most influence on rail track degradation. However, this model may be hard or impossible to use in some cases, as the sections of the rail change along the rail route (i.e. straights, curves, crossovers) and measurements of all the variables are required to develop a mechanistic model.
On the other hand, a study of settlement based on the mechanistic approach has been developed in Austria using a quality index, which denotes acceleration in the vehicle caused by track irregularities [3]. This index comprises both horizontal and vertical deviations in tracks with a shortage of super-elevation and speed. The following equation for track quality shows the exponential behaviour of the track quality index over time:
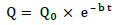 |
(2) |
Where, Q is the track quality index, Q0 is the initial track quality, and b is a constant.
The exponential structure of the Austrian degradation model shows that an increase in the roughness of the track results in more dynamic forces on the rail track. These forces cause deformation of the track geometry, which in turn, increases the variations of the train/track interaction forces and speeds up the track degradation process.
Overall, mechanistic models reflect the actual physical interactions within materials or variables affecting the rail track structure that cause degradation. Following these types of models can be challenging, intensive and time consuming, as materials are not homogenous and the variables of rail track components may be difficult to measure or are poorly understood throughout the model network. In the literature review, few recent studies were found on mechanistic models, and the lack of recent mechanistic studies shows a clear need for further research. Table 1 shows a summary of the variables of mechanistic models, and their strengths and weaknesses.
| Approach | Variables | Strengths | Weaknesses | |
|---|---|---|---|---|
| Mechanistic | • Track settlement, • Track deformation, • Track geometry (e.g. gauge), • Track Quality Index (TQI). |
• Based on laboratory experiment data sources, • Clearly address track settlement and degradation, • Suitable for maintenance of a particular section of rail track. |
• Challenging, intensive, time consuming. • Measurement of the affecting variables of rail structure may be difficult or poorly understood. • Materials of rail structure are not homogenous. • Difficulties in applying the model for different sections of rail track. |
|
| Statistical (Empirical) | Deterministic | • Traffic volume, • Dynamic axle, • Speed, • Accumulated tonnage (MGT), • Axle loads. |
• Work well for large data sets. | • Potential to miss important degradation factors during application, • It does not account for uncertainty (i.e. input parameters and model geometry are not well known). |
| Probabilistic | • Speed restrictions or line closure, • Track Quality Index (TQI), • Standard deviation of longitudinal level defects (SDLL) and horizontal alignment defects (SDHA), • Number of cracks missed by USI per year, • Rail breakage. |
• Reasonable procedure and realistic findings, • Ability to deal with large numbers of datasets to achieve more accurate results. |
• Not common due to lack of historical data, • Difficulties in predicting probability of track deterioration, • Bayesian models rely on Markov models especially when high numerical dimensions occur. |
|
| Stochastic | • Time, • Degradation rate of longitudinal level. |
• Ability to deal with large numbers of datasets to achieve more accurate results, | • No evidence to validate the claim of an exponential deterioration pattern. | |
| Mechanical-empirical | • Track Quality Index (TQI), • Traffic parameters, • Maintenance parameters (EMGT), • Degradation Coefficient [58], • Time. |
• Applicable to different track segments (e.g. curves, turnouts, straight lines), • Applicable to more accurate and less costly future maintenance procedures. |
• Showing a higher rate of deterioration of lines in bridges, curve-bridges and turnouts in comparison with other model types. | |
| Artificial Intelligence | Artificial Neural Networks (ANNs) |
• Number of layers, • Nodes, • Type of the network and functions. |
• Calibrating model with an optimization algorithm, • Optimising parameters of model. |
• Presence of many effective factors resulting in more errors, • Validation of membership functions. |
| Neuro-Fuzzy | • Fuzzy sets, • Fuzzy membership functions. |
• Finding fuzzy rules from numerical data, • Considering human imprecise perception, • Categorising variables into different categories |
• Complexity in abstracting fuzzy rules, • Connections of a proposition may be imprecise, • Difficulty in calibrating model parameters. |
|
2.3.2. Statistical (Empirical) Models
Statistical models have been widely applied in rail degradation prediction. They are based on observations of the rail track structure and the influencing factors, such as traffic, track components and maintenance variables. Hence, these models try to simulate real-life conditions with mathematical equations to predict the future behavior of rail track and its degradation. Statistical models can be classified into three sub-types: deterministic, probabilistic and stochastic (see Fig. 2).
2.3.2.1. Deterministic Models
Deterministic models are usually applied to phenomena where relationships between components of the rail structure are identified. Linear and exponential forms of deterministic models were the first attempt in rail degradation modelling, due to their simplicity in mathematical expressions and ability to show a direct relationship between the input and output variables [26]. Using a mathematical or statistical expression, deterministic models can identify the relationship between the factors affecting rail degradation and the condition of the track. Hence, these models predict the condition of the rail and its degradation deterministically by ignoring random errors in prediction.
Deterministic models require different data parameters, including train speed, geometry and the operations of the rail (i.e. axle weight, line speed and traffic volume) [27] and accumulated tonnage (MGT) [2, 15, 28]. By using data on rail conditions, the deterministic approach provides a general pattern of the statistical distribution of the rail and the affecting parameters.
Deterministic models following a linear relationship are commonly used [2, 15, 29], even though some studies have found a non-linear relationship based on other forms of the model such as polynomial [30], exponential [31] and multi-stage linear [14].
The Office for Research and Experiments (ORE) of the International Union of Railways (UIC2) studied the fundamentals of the degradation mechanism of rail tracks in the 1980s [32]. A deterministic ORE model was proposed to estimate rail degradation according to various studies [33-36]. Accordingly, traffic volume, dynamic axle and speed are the important variables/parameters influencing rail track degradation. The structure of the ORE deterministic model is as follows:
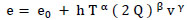 |
(3) |
Where, e0 is the degradation directly after tamping, h is a constant, T is the traffic volume, Q is the dynamic axle, v is the speed, and α, β, and γ are parameters estimated from experimental data.
Basically, the deterministic approach uses railway track geometry data to contribute to the understanding and management of the long-lasting deterministic model. However, although this model may work well for large datasets, the rate of degradation may vary, which may affect the asset management of the track. Moreover, this type of model does not account for uncertainty. In other words, the parameters governing the equations are assumed to be known and the solutions are hence unique. Therefore, even if the methodology of the deterministic models is understandable and simple, it is difficult to trust the results of these models because the input parameters and the model geometry are not well defined. In addition, these studies potentially miss an important degradation factor during application. Therefore, more research is needed for further analysis (a detailed summary is shown in Table 1).
2.3.2.2. Probabilistic Models
Various probabilistic models have been proposed, although it is difficult to analyse the probability of track degradation due to a number of factors, such as the environment, the structural materials and the construction quality. Probabilistic models can be grouped into three classifications (Fig. 3).
- Continuous Probability Distributions
Continuous probability distribution models are usually applied in certain states and within a known elapsed time since the last maintenance activity. A study by Jernbaneverket (JBV), the Norwegian National Rail Administration, was carried out using a probability distribution model [37]. This study calculates the risks and costs of rail defects and outlines the issues of rail failure by using the inspection and maintenance strategies followed by the railway company [37]. It was found that time, speed and rail route location are the variables, which most affect rail degradation using the continuous probability distribution model.
Following equation presents the model, which evaluates the probability of rail breakage of detecting a crack.
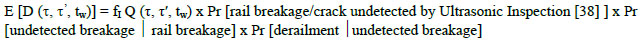 |
(4) |
Where, E[D(τ, τ’, tw)] is the expected number of derailments per year, fI is the yearly frequency of crack initiations, Q (τ, τ′, tw) is the number of cracks missed by USI per year and τ, τ’, tw are different variables directly related to rail derailment, including time, speed and route of the railway.
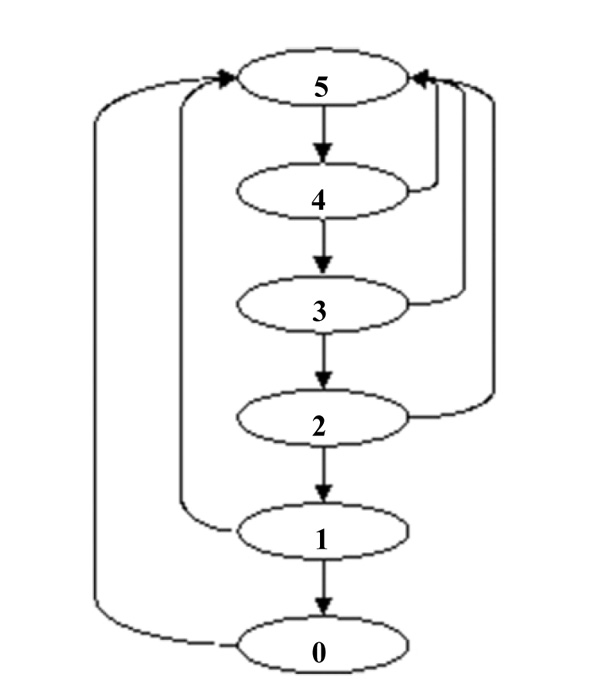
Another continuous probability distribution model was proposed by Zio et al. [39], defining the progression of defects according to the Norwegian National Rail Administration (Jernbaneverket, JBV). A probability distribution model was applied within a multi-state perspective. In other words, each rail track section is analysed in different discrete states, depending on the rail track degradation and its conditions. Fig. (3) shows a state diagram of the defects using this degradation model. There are 6 sections in this diagram; the rail track condition hj in each section j (j = 1, 2, …, n) is discretised in δ + 1 = 6 levels. Level 5 corresponds to a section with zero defects (i.e. perfect condition). However, the degradation levels hj (hj= 1, 2, 3, 4) correspond to gradual critical rail conditions. Level hj = 0 corresponds to rail breakage (i.e. complete failure). The downward and upward arrows in the diagram correspond to the stochastic transitions of defect growth and repair, respectively, as shown in Fig. (3) [39].
Overall, the purpose of the probability distribution model is to inform realistic and reasonable decision-making on inspection and maintenance optimisation practices in the railway industry. The study of this model found that the growth of defects depends on the expected times of failure, which sort the defect as ‘high risk’ or ‘low risk’. Failure also depends on the speed at which trains pass over the track. Although there have been a number of recent continuous probability distribution studies, this model is recommended for use in a certain state and within a known time frame.
- Hierarchical Bayesian Models
Hierarchical Bayesian Models (HBMs) are flexible statistical models that provide a general prediction of railway track geometry degradation. HBMs allow the assessment of the relationship between different components of consecutive rail track sections, including the deterioration rates and the initial qualities parameters. For example, a study of an HBM was developed for the main Portuguese railway line Lisbon-Oporto, assessing two main quality parameters in relation to the degradation of rail track geometry, which are the Standard Deviation of Longitudinal Level defects (SDLL) and the Standard Deviation of Horizontal Alignment defects (SDHA) [40]. This model adopts the parameters as random variables that can be uncertainly calculated by a prior distribution [40]. This prior distribution P(θ) is then combined with the traditional likelihood p(y|θ) to obtain the posterior distribution of the parameters of interest [40]. The posterior distribution P(θ|y) of the parameters θ given the observed data y can be calculated according to Bayes' rule as presented in the following equation:
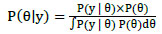 |
(5) |
Where, θ is the initial quality parameter, y is a random variable, the value or probability distribution of which is known, P(θ | y) is posterior distribution of θ given y which relates to θ via a model, P(y | θ) is the likelihood to observe y given unknown θ or the sampling distribution of D given known θ, and P(θ) is the prior probability of θ.
It was found that the calculation of the prior distribution is a vital step in every Bayesian model study. Nevertheless, every case using this model shows that the joint posterior distribution p(θ|y) has a rational high dimension and combination through numerical methods must rely on Markov Chain Monte Carlo (MCMC) methods, which are built such that their stationary distribution is the desired posterior distribution [40-42].
Using HBMs on a sample of operation and maintenance data indicated that they present a worse fit of the quality indicator SDHA compared to the quality indicator SDLL. Horizontal alignment defects also appear to be less predictable [40]. This literature review found that Bayesian model case studies are limited in the published research. They also rely on Markov models, especially when high numerical dimensions occur. Other studies have also developed Bayesian models, including those of [41-45].
- Markov Models
Markov models are statistical models that assess the infrastructure of rail tracks at various condition levels over time. They also analyse the hazard degradation rate while assessing the uncertainty of rail track degradation. The main task of developing a Markov model is to calculate the transition probability from the sampling data. Some calibration techniques are usually used to calibrate the data and calculate the transition probability matrix. Hence, these techniques can be divided into state-based Markov models and time-based Markov models. State-based models are the main focus in this literature as they are commonly used in previous rail degradation prediction studies. For instance, Shafahi and Hakhamaneshi [36] developed a state-based Markov model computing the Track Quality Index (TQI) in a range between 0 and 100 (mapped onto 5 states) based on different parameters including track unevenness, twist, alignment and gauge measurements. The structure of the model is based on a transition matrix showing the probabilities of various states of rail tracks at any time, n, as follows:
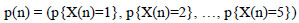 |
(6) |
Where, X(n) is the track state at time n, p{X(n) = j} is the probability that a track is in state j at time n.
Shafahi and Hakhamaneshi [36] found that the Markov model appears to be superior to conventional regression models, such as the ORE model (refer to Section 2.3.2.1). Although further studies and enhancement of the model are desired, the use of the Markov model on Iranian railways has been shown to be a reasonable method for the allocation of maintenance funds [36].
Lyngby et al. [3] also analysed a 50-state Markov model on Norwegian railway tracks. This study considered the twist on each section of the track up to 50mm, with the intention of assessing the failure rates over the railway line. Moreover, this model analysed the deterioration rates depending on the geometry of the track section, whether it was straight, curved or transition. It also analysed the frequency optimisation between track geometrical sections [3].
Another stated-based Markov model was proposed by Prescott and Andrews [46], who studied the degradation, inspection and maintenance of a single one-eighth of a mile section of UK railway track. The model analyses the changing deterioration rate and maintenance of the rail track section. It also studies the effects of changing the level of rail geometry degradation, starting from the good condition of the rail until it reaches the critical value at which maintenance is required.
Overall, probabilistic models are not common, due to the lack of historical data and research related to the geometrical quality of rail tracks. This might be due to the difficulty of predicting the probability of rail degradation. There are also limitations of Markov models, as they are effectively applied to small rail track sections and based on certain states. Moreover, the transitions between states using Markov modelling might face a problem as they must occur at constant rates [3]. This, in turn, restricts the details of the model analysis (as shown in Table 1).
2.3.2.3. Stochastic Models
Stochastic models are mainly statistical models based on historical records and data [47]. They aim to understand the distribution of time to degradation events and predict their performance. These models are based on what has actually happened and account for variability through the use of probability, although they do not deliver insight into the underlying physics [47].
Various research studies have developed stochastic models for rail degradation prediction. Rail characteristics (i.e. rail type, sleeper type), time and rail geometry (including tamping activities) are the main variables used in stochastic modelling. Yousefikia et al. [24] proposed a review of stochastic models based on their data analysis of rail tracks along tram routes in Melbourne, Australia. From this study’s viewpoint, the rail track is considered to be regular when it carries out its function under operating conditions for a certain period of time; if this is not the case, the rail track fails [24]. Hence, the failure progress can be identified in several ways. The gamma process is the most common model used for failure progression and continuous time stochastic processes. Refer to [48] for further details on systems with gamma deterioration activity.
Lyngby et al. [3] also analysed Markov and stochastic degradation models. They stated that rail track geometry could be displayed in a better way as a stochastic model due to the observed variability [3]. Other rail degradation prediction and maintenance planning studies have used stochastic modelling in their research, including [49-54].
A study carried out by Guler et al. [15] analysed a rail geometry deterioration model. This study focuses on the effects of track characteristics, environmental conditions, and maintenance and renewal policies on the deterioration of track parameters measured by recording vehicles. The study determined that natural disasters such as flooding and falling rocks increase the rate of geometry deterioration, whereas snow and landslides have no effect [15]. This study also concluded that the expansion of curvature or gradient or line speed increase the rate of geometry deterioration. This indicates that sleeper type and rail type (Continuously Welded Rail (CWR) or jointed rail) have an influence on geometry deterioration, with CWRs deteriorating at a slower rate [15]. However, the study found that an increase in the annual tonnage reduced the deterioration rates. Therefore, this invalidates the model, as it is known that the increase of the annual tonnage increases deterioration rates.
Quiroga and Schnieder [43] proposed a stochastic degradation model following a heuristic-based method for scheduling tamping intervention, and then developed it into a Monte Carlo simulation for track ageing and restoration. The model is based on 20 years of rail track measurement data collected from the French railway operator SNCF [43]. This model does not take into account data taken in the first three months after an intervention because it assumes that all rail tracks face bedding-in [43]. Hence, only data sets where the time period between tamps was at least one full year were used to raise the precision of the model [55]. However, this assumption reduces the application of this model for the UK network and a number of geometry deterioration practices. The model hypothesis of this study has two assumptions:
- The degradation value NLinitn is achieved after the nth tamping intervention. It is defined as a log-normally distributed stochastic variable:
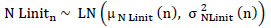 |
(7) |
Where, μ is the mean value, and σ2 is the variance.
- The evolution of the degradation value between two tamping activities. It is defined by an exponential function of the form:
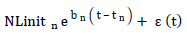 |
(8) |
Where, t is the time, tn is the time at which the last tamping activity took place, bn is a log normally distributed stochastic variable of equation bn ~ LN (μb (n), σb2 (n)), and εn(t) is a normally distributed variable with mean value 0 of equation: εn(t) ~ N(0,σε2.
Although it is assumed in this model that the track undergoes exponential deterioration, there is no evidence to validate the claim of an exponential deterioration pattern. Therefore, the plots of the SNCF rail network sections shown in the results do not indicate that the track geometry undergoes an exponential deterioration pattern [43].
In addition, Andrews [47] developed a Petri net stochastic model to analyse the degradation, inspection, maintenance and renewal of rail track sections. This model studies the efficiency of the asset management process employed and predicts the state of the track geometry. Statistical distributions of times to given levels of geometry deterioration are applied, taking into account the effects of maintenance on the rate of deterioration. However, a better understanding of the degradation process needs to be established. Subsequently, this could support the development of accurate models based on historical data such as the effects of maintenance data [27].
Vale and Lurdes [56] developed a stochastic model of geometrical track degradation using the Portuguese railway Northern Line as a case study. Statistical and probabilistic analyses were achieved for different vehicle speed groups, showing that the rate of degradation of the standard deviation of the longitudinal level is similar for both rails. The degradation rate of longitudinal level has an asymmetric distribution with heavy tailedness shown as:
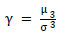 |
(9) |
Where, γ is the skewness of a random variable X, μ is the third moment about the mean, and σ is the standard deviation of the variable.
In this case, the Dagum distribution, usually adopted for representing income distribution, fitted very well the geometrical track degradation activity of the Portuguese railway Northern Line in terms of the longitudinal level [56]. The Dagum distribution represents the model in the analysis of three parameters of function F(x), defined as:
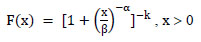 |
(10) |
Where, α, β and k are positive parameters, parameter β is a scale parameter while α and k are shape parameters.
In general, stochastic models are widely used in deterioration prediction studies. However, these models require more understanding of the application used and more explanation of it (see Table 1 for a summary of details). In turn, this can increase the accuracy of these models and their application.
2.3.3. Mechanical-Empirical Models
Mechanical and empirical models are a combination of mechanical and statistical models. These models are based on an understanding of the behaviour of a system’s components, coupled with direct observations, measurements and extensive data records. These models have been used around the globe in order to develop degradation models for railway tracks.
For example, Sadeghi and Askarinejad [57] conducted comprehensive research to improve current track degradation modelling techniques by utilizing thorough field investigation. For the research they followed a mechanical empirical approach and as a part of it they collected a comprehensive volume of rail track field data, which they analysed over a period of two years on a strip of approximately 100 km of railway line in central Iran [57]. In the research, the main parameters that affect the rate of track degradation are grouped into three categories: track quality indices (TQIs), traffic parameters, and maintenance parameters.
Under the traffic parameters the researchers used Equivalent Million Gross Tons (EMGTs) passing the track in a time period (T) at average running speed (v). During major maintenance they considered operations time (T) as a key maintenance parameter. In this study, for the Track Quality Index (TQI), the researchers used the track geometry index (TGI) and the Track Structure Index (TSI). These two indices are not independent variables. In fact, the TGI indicates the geometric conditions of the rail track, such as profile, twist, gauge and alignment, which may directly influence the riding comfort of the track, while TSI represents the mechanistic conditions of the track, such as the condition of the rails, sleepers, fastening systems, sub-grade and even the drainage system.
Some mathematical expressions were developed in this research for modelling the correlation between the main effective parameters and the rail track degradation coefficient [58]. They used data gained from observing the rail track over a period of one year. Therefore, the proposed equations demonstrate the change in DC over time. The equation was further developed into a rail degradation model by combining the constructed correlations between the degradation coefficient and rail track quality, loading and maintenance conditions [57].
The degradation model is displayed in two equations in the paper. These two equations are based on the data from observations of track geometry decay over time and on visual inspections of the mechanistic conditions of the elements of the rail track, as shown below:
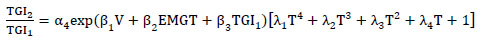 |
(11) |
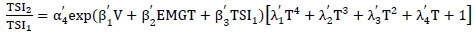 |
(12) |
Where, TGI1 is the Present Track Geometry Index, TGI2 is the Future Track Geometry Index, TSI1 is the Present Track Structure Index, TSI2 is the Future Track Structure Index and T is time. The researchers also developed an equation representing the correlation between the TGI2 and TSI2 due to the limitations of carrying out both inspections. The equation is as follows:
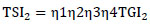 |
(13) |
Where, η1 to η4 are factors representing the influence of train speed (v), EMGT and time (T). Obtaining a linear correlation between the ratios of TGI2/TGI2 and influencing parameters, the following expressions are obtained for η1 to η4:
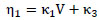 |
(14) |
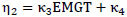 |
(15) |
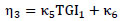 |
(16) |
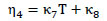 |
(17) |
Where, κ1 to κ8 are constant coefficients.
In their research they were careful to develop separate degradation models for curves, turnouts, straight-line sections, tunnel lines and bridge lines, because of the variation in the behaviour of the rail track at different sections.
Ahac and Lakušić [38] used a similar approach in their study of tram rail track maintenance planning using gauge degradation modelling. This study was carried out in Croatia at the University of Zagreb. The researchers used a mechanical-empirical model in order to determine the rate of degradation through statistical regression analysis. Regression defines the degradation speed of the dependent variable (track quality) and the independent variable (the period of track exploitation). Indirect elastic rail fastening and stiffer direct elastic rail fastening were the two types of rail track systems observed during the study [38].
The results produced by the proposed model indicated that the correlation between the rate of rail track gauge degradation during exploitation and the stiffness of its fastening system can be described by dividing the results into three groups as follows:
- Values of rail track exploitation intensity to approximately 35million gross tons (MGTs),
- After increase in exploitation intensity above 35 MGT,
- For values of the rail track exploitation intensity above 45 MGT.
For values near 35 MGT of rail track exploitation intensity, models for both observed systems estimate equal regression coefficients with very high determination coefficients (0.95 ≤ R2 ≤ 0.98). It was concluded that in the initial stages of rail track exploitation, the effect of fastening system stiffness on the rate of gauge degradation is negligible [38].
After an increase in exploitation intensity above 35 MGT, the gauge degradation speed significantly decreases on tracks with direct elastic fastening systems on tracks with direct elastic systems, while reduction in gauge degradation rate occurs at above 45 MGT of exploitation intensity. Finally, for values of rail track exploitation intensity above 45 MGT, the proposed models do not provide an accurate prediction of gauge degradation behaviour.
In brief, modelling results show that the period of notable gauge degradation during rail track exploitation is shorter in the case of the indirect elastic fastening system with lower stiffness. Therefore, to optimise rail track maintenance procedures and extend the life cycle of rail tracks, it would be desirable to adjust the rail track geometry quality control and maintenance cycles according to rail track stiffness. In addition, when selecting structural elements for new rail tracks, preference should be given to indirect elastic rail fastenings.
According to the authors, the research was limited by the availability and form of the input data on the rail tracks, which were needed for the creation of the database on which the modelling was based [38]. This may have caused a lack of accuracy of the prediction models. Therefore, increasing the accuracy of models requires further monitoring of rail tracks (Table 1).
2.3.4. Artificial Intelligence Models
Artificial Intelligence (AI) models are a modern type of approach used around the world in order to predict degradation in civil engineering. They are on the verge of becoming popular among researchers who work on railway track degradation modelling in the modern era. Although these models are relatively new to civil engineering research, they have been utilized in other disciplines of engineering, such as mechanical engineering. These types of models are well recognized for the high accuracy of predictions they provide.
AI models use the majority of their data to train the model. In most occasions, the model developers use 70% of the data for training their models while the rest of the 30% uses for testing. This makes a strong positive impact on the accuracy that they produce in the results provided by AI models.
According to the literature on rail track degradation prediction, we can categorise AI models into two subcategories: Artificial Neural Networks (ANNs) and neuro-fuzzy models. ANNs are based on the knowledge of biological neural networks. They can be utilized to estimate functions that depend on a large number of inputs and unknowns. These models are generally presented as a system of interconnected neurons. They are there for carrying messages between each other. These connections have a weighting that can be adjusted based on experience, making neural networks adaptive to inputs and capable of learning. The basic structure of a neural network consists of at least three layers, the input layer, the hidden layer and the output layer. Once the data are fed into the input layer the neurons carry the data into the hidden layer to process it and then finally they move to the output layer to produce results. Neuro-fuzzy models are a combination of ANNs and fuzzy logic. These hybrid intelligent systems combine the power of the human-like reasoning style of fuzzy systems with the learning and connectionist structure of neural networks. Both of these model types produce results with high accuracy compared to other models such as mechanical and statistical models.
Shafahi and Hakhamaneshi [36] presented studies including a comparison of four models. The four models included one mechanistic model suggested by the Office for Research and Experiment [32] of the International Union of Railways and three new models: the Markov chain model, ANN and Neuro-fuzzy models. This particular study was conducted at Sharif University of Technology in Tehran. The ORE model was used as a guide in order to compare the results of the new models and the ORE model which was customized with some changes to make it suitable for this study [36]. In the study, the rail track’s state was defined in terms of the Combined Track Record index (CTR) rating out of 100, where the best possible rail track condition was 100 and the states were defined as five intervals of CTR. The data used in the study were obtained from the Iranian railway network [36]. Refer to Table 1 for a summary of AI models.
2.3.4.1. Artificial Neural Networks (ANNs)
Shafahi et al. [55] assumed that the rail track started its life at a time where it was in perfect condition and was then subjected to a sequence of duty cycles that caused its condition to deteriorate. It was also assumed that the duty cycle of the rail track was one year. CTR was also used to define the rail track condition. The following factors were used as effective parameters of rail track degradation in the study:
- CTR index of a year, the previous year, and two and three years before, which was classified from 1 to 5 [55].
- Traffic volume was divided into two groups: light and heavy.
- Maximum allowable speed was classified into 5 classes as follows: maximum speed less than 60 km/h class 1; 60-80 km/h class 2; 80-100 km/h class 3; 100-120 km/h class 4; and more than 120km/h class 5.
- Geographical location was classified into three classes: plain, hilly, and mountainous.
- The maximum gradient of the block was classified into five classes as follows: maximum gradient from 0% - 0.5% gradient class 1; 0.5% - 1% gradient class 2; 1% - 1.5% gradient class 3; 1.5% - 2% gradient class 4; and 2% -3% gradient class 5.
- Minimum radius of curves in the blockwas classified into 7 classes as follows: maximum radius of curves less than 250 m radius class 1; 250 - 400m class 2; 400 – 750m class 3; 750-1000m class 4; 1000 – 2000m class 5; 2000 – 4000m class 6; and radii larger than 4000m class 7.
The following steps were undertaken to build the structure of the ANN model:
Step 1: The topology of the network was created with the inclusion of parameters such as number of layers and nodes of the network, type of network, initial and activation functions.
Step 2: On the basis of the training process in the network, the weighted parameters were corrected and the data on every situation as training data were shown to the network many times.
Step 3: The neural network was examined using known data so that probable errors could be corrected.
A network with 3 layers and 5 neurons in the internal layer was selected as the optimal network. Then the data were randomly directed into two sets: the training set which included 82% of the data, and the test set with 18% of the data. Shafahi et al. [55] showed a comparison of the model predictions and the observed data for one of the sample data sets used. The predictions of the ANN indicated that the following year CTR indices were at the level of the CTR of the previous year or one level lower. Therefore, it was concluded that there was 67% correctness of neural network results using correct sample sets, while there was 33% correctness within one level wrong [55].
Another study carried out in Turkey by Guler [59] indicated excellent results by using an ANN model to predict rail track degradation. This study was a case study for Turkish state railways. The researcher conducted a thorough field investigation over a period of 2 years. The observed track length for this study was approximately 180 km. The dataset was collected based on different variables, including track structure, traffic characteristics, track layout and environmental factors. The author developed separate ANN models for the main track geometry parameters, and performed sensitivity analysis to calculate the importance of each predictor in determining the neural networks.
The neural network was developed using SPSS software and used 70% of the total data from 2009 to 2011 was used as the training data and the remaining 30% for testing. ANN models produced strong relationships between the deterioration rate and the variables. The R2 given as twist=0.727, gauge=0.795, alignment=0.765, cross level= 0.831 and longitudinal levelling =0.742
These results again indicate that ANN could be used as a better alternative for rail track degradation prediction than other models.
2.3.4.2. Neuro-Fuzzy Models
Shafahi et al. [55], developed the ANN model in an effort to compare the accuracy of it by comparing the results produced through that model to few other different models. This study showed that there was 73% correctness of neural network results using correct data sets, while there was 27% correctness with one level wrong [55]. When comparing the results of these two AI models, it was clear that the neuro-fuzzy model showed results 6% better than the ANN model [55].
Neuro-fuzzy models are becoming as popular as ANN models among researchers and look promising for degradation modelling in the future for a number of reasons. The main reason is that they show high accuracy compared to other approaches. The major drawbacks of these models are the lack of literature since they are relatively new to degradation prediction. In addition, it is hard to understand the structure of the models and how they work. They lack the transparency of other models, such as statistical or mechanical models. This discourages researchers from using them in their studies (Table 1).
Based on the literature review, it is possible to conclude that all existing degradation models have a number of strengths and weaknesses. The selection of the most suitable degradation model depends on the research area and the data sets provided to researchers. Table 1 below shows a brief outline of the strengths and weaknesses of each degradation model discussed in the review. It also shows the variables used in each model to help with decision-making on the most appropriate degradation model for any particular research.
3. LIMITATIONS OF EXISTING STUDIES
This literature review shows that there is great variation in rail degradation models. A number of strengths and weaknesses were found for each type. In mechanistic models, various parameters are used, including track settlement, track deformation, heavy haul narrow gauge, high standard gauge and track quality index. These models have a number of strengths, being based on laboratory experimental data. They clearly address track settlement and degradation. In addition, mechanistic models are suitable for the maintenance of a particular section of the track, as we can divide the track into sections, which may give more accurate results. However, sections of the track may vary along the rail (i.e. turnouts, straight lines, curves). Hence, mechanistic models may be hard or impossible to apply. Furthermore, we conclude that these models’ networks are ineffective and inconvenient in many research case studies. The review shows that older studies were found using these models, whilst recent research studies using these models are very rare. Therefore, further research and focus of new trains systems and models is needed for the detection of track damages. For example, SkyTran is one of the latest transportation systems that need to be regularly supervised and checked for any damaged tracks along the rails to prevent fatal crashes. Wiseman [60] suggested a safety mechanistic tool for a continuous inspection of SkyTran tracks by using a digital camera producing JPEG pictures. An automatic analysis of this inspection can indicate whether the tracks are damaged and accordingly repairing the track segment if needed.
In relation to the statistical (empirical) approach, our review classifies this approach into three model types. The first type is the deterministic approach, which concentrates on the following parameters: traffic volume, accumulated tonnage (MGT), axle loads (in metric tons), dynamic axle and speed. Deterministic models work well for large data sets, and are attractive for track degradation modelling. However, certain weaknesses discourage their use. The rate of degradation of deterministic models varies between track sections; it does not apply in the same way on used and maintained tracks, even if they are operated under the same loads. Deterministic models also suffer from the potential to have missed an important factor in the causality of degradation, which in turn invalidates them.
The second type of statistical models is the probabilistic approach, which includes continuous probability distribution models, Bayesian models and Markov models. In our review, different variables were the keys to probabilistic model studies, as follows:
- Speed restrictions (spd) or line closure (cls),
- Track quality index (TQI),
- Standard deviation of longitudinal level defects (SDLL) and standard deviation of horizontal alignment defects (SDHA),
- Number of cracks missed by USI per year,
- Rail breakage.
Based on these variables, a number of strengths and weaknesses exist in relation to each type of probabilistic model. First, we conclude that continuous probability distributions follow a reasonable procedure and offer more realistic findings. However, as mentioned earlier, these models are recommended for a certain state and within a particular timeframe. Second, Markov models deal with large numbers of observational datasets in order to achieve more accurate results. Despite this, there are limitations of Markov models, such as the restriction of analysis details. In other words, this model type is limited to small track models, and the transitions between asset states must occur at a constant rate. In addition, although Bayesian model research studies are limited, they rely on Markov models when high numerical dimensions occur. Overall, our review shows that probabilistic models for rail track degradation are not common, due to the lack of historical data related to the geometrical quality of tracks for research purposes. We also do not ignore the difficulty that researchers may face in predicting the probability of track deterioration.
The third type of statistical models is stochastic modelling, which varies according to the time and the rate of degradation of the longitudinal level. Stochastic models are widely used in degradation prediction studies. They also deal with large numbers of observational datasets to achieve more accurate results. However, these models may need more explanation and understanding of the process. Therefore, we suggest further research and case studies should be applied using these models.
In mechanical-empirical models, track quality index, traffic parameters, maintenance parameters (i.e. Equivalent Million Gross Tons (EMGTs)), degradation coefficient and time are the main variables used. The mechanical-empirical approach provides model development for different track segments, such as curves, turnouts, straight lines, tunnel lines and bridge lines. However, the deterioration of lines in bridges, curve-bridges and turnouts shows a higher rate in comparison with other types; therefore, this model requires more attention, especially in maintenance and inspection scheduling [61]. Although few research papers were found on this model type, it is still applied in different case studies to result in reduced costs of future maintenance practices.
Finally, AI models including ANNs and neuro-fuzzy models depend on different variables, such as the number of layers and nodes, the type of network and fuzzy parameters. These models are the most modern models in deterioration studies. However, few research papers were found using them, as they are new in this field of research.
CONCLUSION
The aim of this paper has been to provide transport agencies, transport appraisal practitioners, and academics with relevant information about the state-of-the-art of different degradation models used in railways. Transport agencies may find it particularly relevant when revising their guidelines for transport appraisal.
Overall, this literature review is a status report on various types of degradation models for urban rail tracks and their influence in maintenance decision-making. It provides relevant sources of information on degradation models, highlighting their parameters in order to compare their strengths and weaknesses. This will help in making decisions about the most appropriate degradation models for use in future research studies.
Based on Table 1 summarising the different degradation models, we consider that stochastic models may be the most suitable type for the majority of case studies. The strengths of these models outweigh their weaknesses. In addition, the strengths of these models outweigh the strengths of other models. However, it should be noted that there are some gaps in existing studies. Therefore, we wish to highlight several promising areas for future research. First, it would be interesting to study factors influencing rail track degradation. The majority of studies briefly mention factors affecting rail degradation without focusing in depth on them. It would also be interesting to develop a degradation model based on these factors. Another important topic we need to consider is a further study on stochastic models. These models need further explanation of their application for a better understanding of them. Limited research has been conducted on the maintenance of rail tracks after the application of degradation modelling. Hence, we suggest further studies in this area to improve the maintenance stage after degradation occurs. This may also improve research into optimising the planned maintenance of rail systems. Since there are now several years of data on the degradation of rail tracks, comparisons with survey work can start to be done to fill the knowledge gaps revealed by this review.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


