All published articles of this journal are available on ScienceDirect.
The Extent of Capacity Loss Caused by Rainfall at Signalised Intersections
Abstract
Background:
Even though their physical characteristics exert a constant influence on capacity and saturation flows, signalized intersections are fixed facilities not affected by rainfall. Whilst traffic conditions with varying effects can be regulated, rainfall conditions cannot be regulated but compensated for by warning drivers to reduce speed. Speed reduction has an impact on signalised intersection capacity, whilst signalised intersection capacity is a function of saturation flow, effective green, and cycle time. In this paper, a capacity loss is the differential percentage between ‘with and without’ rainfall scenario.
Aim:
The paper investigated the extent of capacity loss caused by rainfall at signalised intersections.
Methods:
In Durban, South Africa, rainfall data were collected, collated, and correlated with traffic data in a 'with and without' rainfall intensity study. Rainfall intensity was classified according to the rate of precipitation as follows; rainfall intensity(i): light rain (i <2.5mm/h); Moderate rain (2.5mm/h ≤ i < 10mm/h), and heavy rain (10 ≤ i ≤ 50mm/h) as prescribed by the World Meteorological Society.
Results:
Empirical results show that rainfall intensity has an effect on road capacity at a signalised intersection. Generally, for the vehicles going straight, light rain caused a 4.25% capacity loss; moderate rain 9.18% while heavy rain caused an 11.53% capacity reduction. With right-turning vehicles, light rain caused 7.38% capacity loss; moderate rain caused 14.3%, while heavy rain accounted for 19.15% capacity reduction.
Conclusion:
The paper concluded that rainfall at signalised intersections would cause an anomalous capacity reduction. Since the database for the study is small, the paper advocates for further studies based on a broader database to include yellow interval time.
1. INTRODUCTION
Road capacity is the maximum hourly flow rate at which road users can reasonably expect to traverse a point or a uniform section of a roadway during a given time under the prevailing roadway, environmental, traffic, and control conditions [1]. The definition suggests that the capacity of a roadway section is a function of numerous variables. At signalised intersections, capacity is defined as the maximum flow rate that would be observed based on the amount of green time that is available. Thus, capacity at signalised intersections is a function of saturation flow, effective green, and cycle time. Signalised intersection capacity loss in this paper is the differential percentage between ‘with and without’ rainfall scenario. At signalised intersections, traffic lights are used to manage traffic flow conflicts and ensure orderly vehicle movements. When the traffic light is green, vehicles proceed beyond the stop line; when the traffic light turns red, vehicles stop before the stop line. The yellow lights alert the drivers of impending red light or green as the case may be. Signalised intersections, as fixed facilities, are not affected by rainfall. Whilst traffic conditions can be regulated, it is difficult to regulate or predict rainfall. As mentioned in many literatures, road capacity is affected by rainfall. In a study carried out in Tokyo, Japan, highway capacity decreased by 4-7% under light rainfall and 14% under heavy rain [2]. In a study conducted in Waterloo, Canada, rainfall affects both speed and headway; results show a decrease of 3% in saturation flow for the wet conditions, 19% for the wet and slushy [3]. In a South Korean study, results showed that the saturation flow rate was between 87% and 96% of the dry weather under 17-28mm/hr rainfall intensity [4]. In any case, when it rains, drivers reduce vehicle speed and increase the follow-up gap because of poor visibility, poor road surface traction, among others. These changes affect saturation flow, lost time, and signalised intersection capacity. However, the extent to which rainfall can account for capacity loss at signalised intersections is questionable. Consequently, the paper investigated the extent of capacity loss caused by rainfall.
2. LITERATURE REVIEW
The South African Road Traffic Signal Manual-SARTSM [5] defines road traffic signals as “one of the most common and widely accepted forms of traffic control that affect the daily lives of virtually all road users. It can be very effective in improving traffic flow and facilitating access to major roadways. However, traffic signals can also cause significant disbenefit and possible danger to road users when installed inappropriately.” In South Africa, the approach speed at signalised intersections must not exceed 80km/h (22.2m/s) and traffic signal faces must be visible as drivers approach the traffic light. Cycle time is a function of lost time and effective green. It is the total signal time allocated to all signal phases. It is composed of lost time and traffic flow turning proportion. The optimum cycle length is:
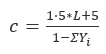 |
(1) |
Where: C = Optimum cycle length (s), L= Total lost time per cycle (s)
Yi = Volume/ saturation flow ratio per critical movement in stage i
Effective green is the amount of good time available to serve vehicular movements during a phase of a cycle. The effective green time for any movement is the sum of the displayed green and yellow time minus the lost time. Given the saturation flow rate, effective green, and the cycle length, the capacity at a signalised intersection is determined. Capacity at a signalised intersection is “the maximum rate at which vehicles can pass through the intersection under prevailing conditions” [6]. This definition suggests that prevailing traffic, road, and weather conditions affect road capacity. In a study on the impact of a heavy vehicle on the capacity of signalised intersections, heavy vehicles have an impact on capacity and delay [10]. The ideal saturation flow rate is defined in Highway Capacity Manual 2010 as the equivalent hourly rate at which previously queued vehicles can traverse an intersection approach under prevailing conditions, assuming that the green signal is available at all times and no lost times are experienced in vehicles per hour or vehicles per hour per lane [1]. HCM 2010 method is the most common method for the determination of signalised intersection capacity.
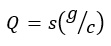 |
(2) |
Where, Q ~ signalised intersection capacity, s ~saturation flow rate, g ~ effective green, and C ~cycle time saturation flow is the key explanatory variable in equation 2. The ideal saturation flow value is considered to be affected by the traffic flow conditions of the intersection approach lane under examination, geometric features, and environmental factors. When the traffic light turns green, vehicles proceed into the intersection from a stopped queue position with headways between successive vehicles as they cross the stop line. The number of vehicles that can pass through a signalised intersection if the green lights were available for one hour without interruption is called the saturation flow.
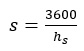 |
(3) |
Where; s ~ saturation flow and hs ~ saturation headway that can be estimated is as follows:
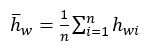 |
(4) |
Where, hw ~average headway; hwi ~headway of vehicle i in the queue, n ~ sample size The Highway Capacity Manual field measurement method involves estimating saturation headway; after about 10s to 14s of green time, which corresponds to the front axle of the fourth passenger car passing the stop line in the saturation headway. Vehicle recording starts when the first vehicle in the queue crosses the stop line, then the fourth and the 14th or last vehicle. The time difference between the 14th(or last) vehicle and the fourth divided by the number of vehicles yields the saturation headway (hs). The saturation flow rate in vehicles per hour (veh/h) or passenger car units per hour per lane (pcu/h/ln) is then obtained by diving 3600 by the average saturation headway. Equation 5 below gives the expressions for saturation headway, respectively.
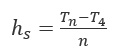 |
(5) |
Where: Tn,4= time nth and fourth vehicle clears the stop line, n = number of vehicles According to Prevedorous and Chang, saturation flow, effective green time, and progression may be affected by wet weather. Saturation headway may lengthen, effective green time may shrink, and progression may worsen [7]. In a study conducted in China using video data to investigate the effect of slight snow (less than 3cm of snow in 24 hours) on signalised intersection capacity, the capacity reduced by 7% and the level of service reduced by one [8]. In a study conducted in Salt Lake City, Utah, USA, saturation flow was reduced by 6% for rainfall conditions and the reduction went up to 20% for snowy conditions [9]. According to Ben-Edigbe et al. [10, 11], headway values greater than 5s are not significantly affected by rain; hence vehicles with headways greater than 5s in this paper were filtered out. In previous studies [11, 12] discharge headway fitted by a lognormal distribution density function is shown below:
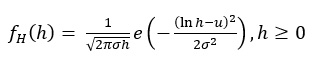 |
(6) |
The degree of saturation is the ratio of volume to the capacity per lane. If the degree of saturation is less than one, then there is sufficient capacity to serve the traffic demand. Generally, when the v/c ratio is less than 0.85, it indicates that there is adequate capacity available and vehicles are not expected to experience significant delays and queues. However, as the degree of saturation approaches 1.0, traffic flow becomes less stable. Under such conditions, vehicles may require more than one signal cycle length to clear the intersection. If the degree of saturation is greater than one, then it means traffic demand exceeds capacity. Generally, the degree of saturation is given by equations 7 and 8 below:
| X = v / Q | (7) |
Since, Q = s*(g/C) and v is expressed as; 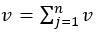
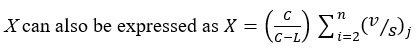 |
(8) |
Where; X= degree of saturation, C = cycle length, L = lost time per cycle; v = demand traffic volume
The lost time in equations 8 and 9 is that part of the cycle time, not utilised because of the change in phase movements. Specifically, the Start-up Lost Time (SULT) is the time lag that occurs when the lights turn from red to green, and the queued drivers do not instantly start to move at the saturation flow rate. Determination of the start-up lost time involves the determination of discharge headways of vehicles in the queue and then summing the differences between the observed headway of a predetermined vehicles (up to 4s for HCM 2010) from the saturation headway.
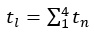 |
(9) |
Where: tL ~start-up lost time, tn ~difference between the discharge of the nth vehicle and saturation headway past studies have investigated both start-up's lost time and effective green. The values obtained for start-up lost time vary from 1s to 2s [13]. Turning movements, queue length, geometry and location, time of day, weather condition, traffic light visibility, phase timing, and sequencing are factors that affect the value for start-up lost time [13]. In a study carried out in Beijing [14, 15], grade 1 rainfall (0-5mm) caused a saturation flow reduction of up to 13% and decreased start-up lost time by 30%. Grade 2 rainfall (5.1mm- 32mm) had a reduction in the saturation flow rate between 13- 30% and a start-up lost time reduction of 50%. The highest grade of rainfall, grade 4(>43mm), led to a 60% reduction in saturation flow and a 100% reduction in start-up lost time. In another study, start-up lost time increased from 2s to 3s [16]. Start-up lost time increased by 23% from 2s to 2.5s and the speed reduced by 30% from rainfall at signalised intersections [16, 17]. What is lacking in these studies is the mention of passenger car equivalency modification caused by rainfall as it has an insignificant effect on the study outcome. What is clear is that capacity loss will result from rainfall at signalised intersections irrespective of intensity. Can the same premise be held in Durban, South Africa? Is capacity loss anomalous or does it follow a pattern of loss relative to intensity?
| Site |
Weather |
Straight | Right Turning | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Effective green (s) | Cycle time | Capacity Veh/h |
v/Q | Effective green (s) | Cycle time (s) | Capacity Veh/h |
v/Q | ||
| 1 |
Dry | 74.17 | 120 | 1373 | 0.47 | 30.26 | 120 | 519 | 0.74 |
| Light | 74.16 | 120 | 1348 | 0.42 | 30.15 | 120 | 484 | 0.75 | |
| Medium | 73.74 | 120 | 1264 | 0.38 | 29.87 | 120 | 413 | 0.85 | |
| Heavy | 73.56 | 120 | 1226 | 0.38 | 29.82 | 120 | 381 | 0.87 | |
| 2 |
Dry | 67.07 | 120 | 1242 | 0.45 | 25.06 | 120 | 418 | 0.78 |
| Light | 66.70 | 120 | 1198 | 0.47 | 24.90 | 120 | 395 | 0.80 | |
| Medium | 66.63 | 120 | 1155 | 0.46 | 24.78 | 120 | 385 | 0.79 | |
| Heavy | 66.60 | 120 | 1110 | 0.34 | 24.63 | 120 | 355 | 0.82 | |
| 3 |
Dry | 53.14 | 100 | 1174 | 0.54 | 30.63 | 100 | 599 | 0.83 |
| Light | 53.10 | 100 | 1138 | 0.52 | 30.59 | 100 | 515 | 0.84 | |
| Medium | 53.04 | 100 | 1097 | 0.42 | 30.27 | 100 | 495 | 0.87 | |
| Heavy | 52.94 | 100 | 1070 | 0.35 | 30.18 | 100 | 477 | 0.88 | |
| 4 |
Dry | 48.10 | 100 | 1056 | 0.58 | 16.00 | 100 | 303 | 1.01 |
| Light | 47.77 | 100 | 966 | 0.55 | 15.97 | 100 | 293 | 1.02 | |
| Medium | 47.74 | 100 | 895 | 0.51 | 15.76 | 100 | 265 | 1.09 | |
| Heavy | 47.58 | 100 | 887 | 0.48 | 15.74 | 100 | 259 | 1.10 | |
3. MATERIALS AND METHODS
Rainfall and traffic data were collected simultaneously and continuously for six weeks between October and December 2019, during the rainy season in Durban, South Africa. Rainfall data were obtained from Durban Meteorological Department and complemented with automatic rain gauge data from stations located within the survey catchment area. The rain-gauge was at 0.20mm/tip. Logged rainfall data were downloaded and exported to an excel sheet using a 5 minutes (0.083hr) time interval, then converted to intensity by dividing with 0.083 to have the intensity in mm/hr. Rainfall intensities were classified as light rain (< 2.5mm/h), moderate rain (2.5mm/h and 10mm/h), heavy rain (10mm/h and 50mm/h) using World Meteorological Organisation classification system. Weighty rain with intensity greater than 50mm/h was not considered due to excessive aquaplaning and drag force effect on tyres.
At selected 4-legged signalised intersections, traffic data were extracted from traffic videotapes obtained from eThekwini Transport Authority, Durban, and verified manually on-site as illustrated in Fig. (1). Note from Fig. (1) that left-turning vehicles use flare lanes without allocated traffic light or time; hence left-turning vehicles were excluded in the analysis, vehicles going straight or turning right were analysed.
All selected four sites have posted speed limit of 60km/h, two sites observed a cycle time of 100s and the other two sites 120s. A summary of extracted traffic data for all sites is shown in Table 1. Traffic volume is converted to traffic flow with modified passenger car equivalent values. The modification is needed because of the effect of rainfall on traffic stream. The determination of passenger car equivalent values remains a subject of debate due to differences in estimation methods. Nevertheless, a simple headway method based on equation ten was used to estimate passenger car equivalent values. It is the ratio of the average headway of the target vehicle to the average headway of the car expressed as;
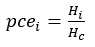 |
(10) |
Where; pcei - passenger car equivalent of vehicle class i; Hi - average headway of vehicle class i (s)
Hc - average headway of passenger car (s); Headway = spacing / speed, and Spacing = 1000m / density
4. RESULTS AND DISCUSSION
Headway between successive vehicles is an essential microscopic flow characteristic that affects road capacity, level of service, and driver behavior. Average vehicle and discharge headways were extracted manually from the video footage. Recordings were taken for vehicles in the initial queue up to a maximum of 14 vehicles. Time is taken by the first three vehicles to cross the stop line (T3), minus time taken by the thirteen vehicles (T13) divided by the number of vehicles less the first three vehicles at the start of the queue. Discharge headways are then tested for statistical fitness. Estimated discharge headways and their statistical fitness are shown in Table 2. The average value of discharge headways is higher than the median value; the range is from 0.00s to 0.06s, which is consistent with the previous findings [18-20]; the skewness of headways is positive. These characteristics indicate that the distribution of discharge headway is likely unsymmetrical, and the normal distribution function is not appropriate to fit the headway data. The lognormal distribution has been found to be the best simple model of the distribution of headways. The fact that the average value of discharge headway is higher than the median value shows that more than 50% of drivers will keep smaller headway, thus suggesting that the saturation flowrate estimation method used probably underestimated the flow rates. Notwithstanding, it will not affect the study outcomes.

| - | Sample size | Average | Median | Standard error | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| Site 1 | ||||||
| Dry | 1500 | 1.42 | 1.41 | 0.053 | 0.01 | -0.56 |
| Light | 400 | 1.56 | 1.54 | 0.043 | 0.36 | -0.16 |
| Moderate | 450 | 1.56 | 1.53 | 0.085 | 0.34 | -0.63 |
| Heavy | 400 | 1.68 | 1.63 | 0.091 | 0.35 | -0.33 |
| Site 2 | ||||||
| Dry | 1300 | 1.53 | 1.49 | 0.053 | 0.50 | 0.16 |
| Light | 150 | 1.60 | 1.58 | 0.043 | 0.44 | -0.16 |
| Moderate | 200 | 1.62 | 1.58 | 0.085 | 0.66 | 0.34 |
| Heavy | 490 | 1.73 | 1.69 | 0.091 | 0.64 | 0.29 |
| Site 3 | ||||||
| Dry | 1000 | 1.52 | 1.51 | 0.053 | 0.31 | 0.09 |
| Light | 280 | 1.68 | 1.60 | 0.043 | 0.61 | 0.25 |
| Moderate | 200 | 1.75 | 1.70 | 0.085 | 0.56 | 0.23 |
| Heavy | 470 | 1.92 | 1.92 | 0.091 | 0.66 | 1.28 |
| Site 4 | ||||||
| Dry | 1400 | 1.56 | 1.54 | 0.053 | 0.39 | 0.23 |
| Light | 430 | 1.61 | 1.55 | 0.043 | 0.83 | 0.76 |
| Moderate | 400 | 1.76 | 1.72 | 0.085 | 0.74 | 0.38 |
| Heavy | 500 | 1.81 | 1.76 | 0.091 | 0.81 | 0.83 |
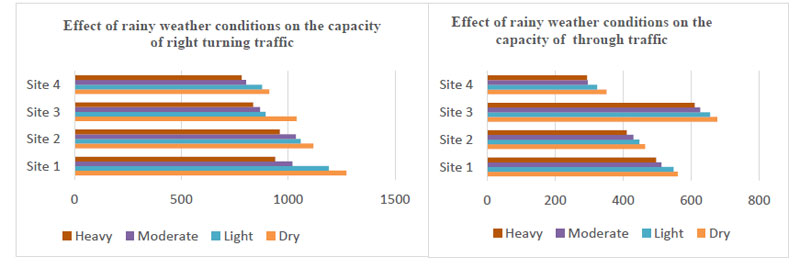
Generally, headways are lower for dry weather than those of rainy conditions in all cases. Analysis shows that headways stabilize after the fourth vehicle. Therefore, the start-up lost time is the difference between the saturation headway and the first four discharge headways. As shown in Table 3, Start-up Lost Times (SULT) for dry weather conditions are lower than start-up lost times for rainfall. Light rainfall has an average increase in start-up lost time of 7.47% (ranging from 0.55% to 19.17%), moderate rainfall has an average increase of 19.72% (ranging from 5% to 26%). Whereas, heavy rainfall has an average increase of 25% (ranging from 10% to 33%). On average, the sites with higher cycle times also have higher values of start-up lost time. These results are within the findings of previous studies [17, 20]. As shown below in Fig. (2) and Table 4, the average saturation flow for vehicles going straight under dry weather conditions is 2200 veh/hr, for light rain (2120 veh/hr), moderate rain (2020veh/hr), and heavy rain (1970veh/hr). Estimated saturation flow percentage reductions for vehicles going straight are 3.6% for light rain, 8.2% for moderate rain, and 10.4% for heavy rain. The average saturation flow reductions for vehicles turning right are 1970veh/hr under dry weather conditions, 1830veh/hr in light rain, 1710veh/hr in moderate rain, and 1620veh/hr in heavy rain. Saturation flow percentage reductions for vehicles going straight are 7.1% for light rain, 13.2% for moderate, and 17.8% for heavy rain. These results are within the limits of previous studies [9]. Generally, saturation flows are higher for dry weather than those of rainy conditions in all cases. The average headway for vehicles going straight at all sites is 1.63s for dry weather and 1.69s for light, 1.78s for moderate, and 1.83s for heavy rainy conditions, respectively. The average headway for right turn movements at all sites is 1.82s for dry weather conditions and 1.96s for light, 2.11s for moderate, and 2.23s for heavy rainy conditions, respectively.
| Site | Approach | Dry Weather | Rainfall |
Cycle time (s) |
||
|---|---|---|---|---|---|---|
| Light | Moderate | Heavy | ||||
| SULT (s) |
SULT (s) |
SULT (s) |
SULT (s) |
|||
| 1 | Straight | 1.83 | 1.84 | 2.26 | 2.44 | 120 |
| Right Turn | 1.74 | 1.85 | 2.13 | 2.18 | ||
| 2 | Straight | 1.93 | 2.30 | 2.37 | 2.40 | 120 |
| Right Turn | 1.94 | 2.10 | 2.22 | 2.37 | ||
| 3 | Straight | 1.86 | 1.90 | 1.96 | 2.06 | 100 |
| Right Turn | 1.37 | 1.41 | 1.73 | 1.82 | ||
| 4 | Straight | 1.90 | 2.23 | 2.26 | 2.42 | 100 |
| Right Turn | 1.00 | 1.03 | 1.24 | 1.25 | ||

From the results shown below in Table 5 and Fig. (3), through traffic capacity is significantly higher than right-turning traffic capacity, generally, for through traffic, light rain caused a 4.25% capacity loss, and moderate rain caused 9.18% loss. In comparison, heavy rain caused an 11.53% capacity loss. For the right turning traffic, capacity loss is 7.38% for light rain, 14.53% for moderate rain, and 19.15% for heavy rain. Although previous studies classified rainfall without intensities nonetheless, the results in this study are within the findings of previous studies [2]. In general, the reduction is higher for right-turning traffic compared to traffic flow. The difference between the through and right turning starts from the lost time and saturation flow rate, which are also affected significantly by rainfall. In practical applications, results can be a part of the Variable Message Signs (VMS) strategic management policy. VMS are electronic and intelligent display panels that allow text and graphic variable messages to be combined, resulting in a more effective means of traffic control mechanism. In order to reduce traffic accidents on roadways, variable message signs give rainfall warning and speed reduction information to the drivers before, during, and after rainfall.
| Site | Weather | Straight | Right Turning | ||
|---|---|---|---|---|---|
| Headway hs |
Saturation flow(pcu/h) | Headway hs |
Saturation flow (pcu/h) | ||
| 1 |
Dry | 1.62 | 2222 | 1.75 | 2057 |
| Light | 1.65 | 2182 | 1.87 | 1925 | |
| Moderate | 1.75 | 2057 | 2.17 | 1659 | |
| Heavy | 1.80 | 2000 | 2.35 | 1532 | |
| 2 |
Dry | 1.62 | 2222 | 1.80 | 2000 |
| Light | 1.67 | 2156 | 1.89 | 1905 | |
| Moderate | 1.73 | 2081 | 1.93 | 1865 | |
| Heavy | 1.80 | 2000 | 2.08 | 1731 | |
| 3 |
Dry | 1.63 | 2209 | 1.84 | 1957 |
| Light | 1.68 | 2143 | 2.14 | 1682 | |
| Moderate | 1.74 | 2069 | 2.20 | 1636 | |
| Heavy | 1.78 | 2022 | 2.28 | 1579 | |
| 4 |
Dry | 1.64 | 2195 | 1.90 | 1895 |
| Light | 1.78 | 2022 | 1.96 | 1837 | |
| Moderate | 1.92 | 1875 | 2.14 | 1682 | |
| Heavy | 1.93 | 1865 | 2.19 | 1644 | |
| Site | Weather | Straight | Right Turn | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Effective green | Cycle time | Saturation flow | Capacity (%) | Effective green | Cycle time | Saturation flow | Capacity (%) |
||
| 1 |
Dry | 74.17 | 120 | 2222 | 1373 | 30.26 | 120 | 2057 | 519 |
| Light | 74.16 | 120 | 2182 | 1348 (1.8) | 30.15 | 120 | 1925 | 484 (6.8) | |
| Moderate | 73.74 | 120 | 2057 | 1264 (7.9) | 29.87 | 120 | 1659 | 413 (20.4) | |
| Heavy | 73.56 | 120 | 2000 | 1226 (10.7) | 29.82 | 120 | 1532 | 381 (26.6) | |
| 2 |
Dry | 67.07 | 120 | 2222 | 1242 | 25.06 | 120 | 2000 | 418 |
| Light | 66.70 | 120 | 2156 | 1198 (3.5) | 24.90 | 120 | 1905 | 395 (5.4) | |
| Moderate | 66.63 | 120 | 2081 | 1155 (7.0) | 24.78 | 120 | 1865 | 385 (7.9) | |
| Heavy | 66.60 | 120 | 2000 | 1110 (10.6) | 24.63 | 120 | 1731 | 355 (15.0) | |
| 3 |
Dry | 53.14 | 100 | 2209 | 1174 | 30.63 | 100 | 1957 | 599 |
| Light | 53.10 | 100 | 2143 | 1138 (3.1) | 30.59 | 100 | 1682 | 515 (14.1) | |
| Moderate | 53.04 | 100 | 2069 | 1097 (6.5) | 30.27 | 100 | 1636 | 495 (17.3) | |
| Heavy | 52.94 | 100 | 2022 | 1070 (8.8) | 30.18 | 100 | 1579 | 477 (20.4) | |
| 4 |
Dry | 48.10 | 100 | 2195 | 1056 | 16.00 | 100 | 1895 | 303 |
| Light | 47.77 | 100 | 2022 | 966 (8.6) | 15.97 | 100 | 1837 | 293 (3.2) | |
| Moderate | 47.74 | 100 | 1875 | 895 (15.3) | 15.76 | 100 | 1682 | 265 (12.5) | |
| Heavy | 47.58 | 100 | 1865 | 887 (16.0) | 15.74 | 100 | 1644 | 259 (14.6) | |
CONCLUSION
The paper investigated the extent of capacity loss caused by rainfall at signalised intersections in Durban, South Africa. The study objectives were met. Effective green, discharge headway, saturation flow, and capacity at signalised intersections under dry and rainy weather conditions were estimated. Modified passenger car equivalent values were used to convert observed traffic volumes to flows. Start-up lost time is an important parameter in the performance of signalized intersections. It depicts the impact of rainfall on drivers’ behavior in South Africa. Start-up lost time is related to the start response time of the lead vehicle in the queue. The parameters affecting the Start-up Lost Time (SULT) in South Africa were defined and a model was established to present the relationship between start-up lost time and saturation flow. In light of detailed analysis, the following conclusions are drawn:
- The average discharge headway values are more significant than the median values and the skew of headways is positive.
- The estimated saturation flow rates are useful in determining capacity loss.
- Rain has a significant effect on the capacity of signalised intersections. The capacity loss for vehicles going straight is lower than right turning vehicles. For vehicles going straight, light rain caused 4.25% capacity loss, moderate rain 9.18%, and heavy rain accounted for 11.53% capacity reduction. For vehicles turning right, light rain caused 7.38% capacity loss; moderate rain caused 14.3% while heavy rain accounted for 19.15% capacity reduction.
The results of this study may be used in the capacity analyses of signalized intersections. However, since the database for the study is small, the paper advocates for further studies on a broader database to include yellow interval time.
List of Notations
| Q | = Capacity, |
| s | = Saturation Flow |
| g | = Effective Green |
| C | Cycle Time |
| hs | = Saturation Headway |
| hw | = Average Headway; |
| hwi | = Headway of Vehicle i in the Queue |
| n | = Sample Size |
| f H (h) | = Lognormal Distribution Density Function |
| E(H) | = Mean of a Lognormal Distribution |
| M(H) | = Median of a Lognormal Distribution |
| V(H) | = Variance of a Lognormal Distribution |
| tl | = Lost Time |
| tn | = Difference Between the Discharge of the nth Vehicle |
| pcei | = Passenger Car Equivalent of Vehicle Class i |
| Hi | = Average Headway of Vehicle Class i (s) |
| Hc | = Average Headway of Passenger car (s) |
CONSENT FOR PUBLICATION
Not applicable
AVAILABILITY OF DATA AND MATERIALS
The authors confirm that the data supporting the findings of this research are available within the article.
FUNDING
The University of KwaZulu-Natal partially supported this work through a 3-year PhD Research Scholarship Number 217079425 Granted to Oyaro Janet; (2017-2020).
CONFLICT OF INTEREST
The authors declare no conflicts of interest, financial or otherwise
ACKNOWLEDGEMENTS
The University of KwaZulu-Natal, Durban, South Africa, funded the research. The research team is grateful to all for their invaluable assistance at the data collection stage.


