Influence of Night Rainfall on Stopping Sight Distance on Dark Roadways
Abstract
Aim:
To investigate the influence of night rainfall on stopping sight distance on dark roadways.
Background:
This study fills the research gap in stopping sight distance by looking at night rainfall impact on stopping sight distance on dark roadways.
Objectives:
To determine stopping sight distance under night rainfall (light, moderate and heavy) on dark roadways and compare the results with stopping sight distance under dry night on dark roadways.
Methods:
In a ‘with and without’ night rainfall impact studies, traffic volume, speed, vehicle type and rainfall data were collected at selected sites. All surveyed sites had rain gauge within the catchment area of about 1km. Rainfall intensity was divided into three groups (light, moderate, and heavy). Dry weather data were used as a control parameter.
Results:
Results show that the average SSD decrease attributed to light rainfall is 15.2m (14%), moderate rainfall 18.3m (16.8%), and heavy rainfall 21.2m (19.2%).
Conclusion:
Based on the results and findings, it is correct to conclude that the effect of night rainfall on dark roadways stopping sight distance is somewhat aberrant. It is also correct to suggest that night rainfall on dark roadways will cause a decrease in perception distance travel delay, an increase in braking distance and stopping sight distance.
1. INTRODUCTION
It has been shown in previous studies that rainfall adversely affects traffic stream performances. According to AL Hassan and Ben-Edigbe, rain poses a major hazard with various impacts on road and traffic performances due to its spatiotemporal nature [1]. Probably the most obvious hazards are decreased visibility and poor tyre traction. Drivers have no control over these hazards. What they can control is how well they handle and react to the ensuing challenges; especially abrupt stopping caused by lead vehicle or any sudden strange object on the roadway. It has been shown in many works of literature that wet road surface and braking distance have a clear correlation with vehicle collisions often rear-end. Previous studies [2-7] focused on static wet road surface under dry weather conditions. Driving during rainfall suggests that the downpour of water on the road surface is continuous and not static. In any case, wet pavement irrespective of how it happened would make tyres have less grip on the road surface, thus ensuing slippery road surface that could trigger an accident. To what extent would stopping sight distance be affected by night rainfall, it may be queried. Previous studies have shown that rainfall affects traffic stream operations by reducing speed, and increasing travel time, inducing capacity loss, and service delivery [3, 6-16]. However, most of the previous studies focussed on daylight condition; where night-time was considered, the roads have lights for illumination. Thus, creating a research gap that the paper is exploring. It is postulated that night rainfall has a significant impact on stopping sight distance of dark roadways irrespective of the reaction time used to determine the perception distance. Bearing in mind that stopping distance is made up of perception distance (the distance the car travels from the point when the driver realises he needs to apply the brakes and braking distance is the distance the car travels from the point when the driver starts to press the brake pedal till vehicle comes to a complete stop.
2. BACKGROUND
Driving at night in the rain on dark roadways has challenges that include stopping sight distance, among others. The primary factors affecting stopping sight distance include driver eye height, vehicle operating speed, pavement coefficient of friction, roadway gradient, deceleration rate, and perception/reaction time, among others. A distinction must be made between driving on wet pavement during rainfall and wet pavement after rainfall. Wet pavement during rainfall has the added challenge of a continuous downpour of rain and poor visibility. Even though years of research and practice have led to vehicle tyre tread which offers good traction, the associated drivers’ challenges have not lessened. In passing, the coefficient of friction varies for different road surfaces under varying prevailing conditions and it correlates with deceleration. It is not necessary to specify both the deceleration rate and coefficient of friction. According to Tromp [13] on dry surfaces, the friction on porous asphalt is less than on dense asphalt. For newly applied porous asphalt maximum deceleration (locked wheels) for new porous asphalt is 6 m/s2, for old porous asphalt 7 m/s2, and 8 m/s2 for dense asphalt. For a dry surface and wet surface, 0.7 and 0.4 respectively according to Jones and Childers [9]. The value could be as high as 0.9 for dry surface and as low as 0.1 for the non-dry road surface. Some studies even reported between 0.28 and 0.4 for wet pavement based on varying design speeds [2, 10]. American Association of State Highway and Transportation Officials -AASHTO’s suggested deceleration rate of 3.4 m/s2 resulting in a friction coefficient of 0.35 for the wet pavement [2]. According to Hall and Turner [17], frictional values used in the stopping distance equation were 0.5 on wet pavement and 0.8 on dry pavement; the latter condition is comparatively rare in Oregon, USA. In the studies conducted by Kordani et al. [14] on the issue of road surface friction factor for different weather conditions, results showed that the friction coefficient in values of 0.9, 0.8, 0.7, 0.6 do not affect braking distance significantly and it is possible to attribute them all to dry weather conditions. However, the values of 0.5, 0.4, 0.28 and 0.18 attributed to wet, rainy, snowy and icy conditions respectively have a significant effect on braking distance. As for reaction time, that it is a component of perception/reaction distance, some accident reconstruction specialists use 1.5s while the average reaction time in most literature is between 2s and 2.5s. Well, since human characteristics are dynamic, the estimation of reaction time need not be fixed, however, an assumption of a fixed reaction is permissible under certain circumstances. What is clear from the postulations so far is that the friction and indeed deceleration are related; speed, reaction and braking distances are key components of stopping sight distance. Braking distance is a significant basic parameter because it is the overall distance travelled by the vehicle from the onset of brake application to the complete halt of the vehicle. It is primarily affected by the original speed of the vehicle and the coefficient of friction between the tyres and the type of road surface. The equation for Stopping Sight Distance (SSD) is Eq. (1);
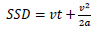 |
(1) |
Where: deceleration is (a), reaction time is (t), and the vehicle speed is (v). As contained in many works of literature, deceleration is speed reduction, and it can be estimated with Eq. (2).
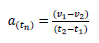 |
(2) |
Where; a = deceleration at time tn, v - speed, and t - time. If Eq. (2) is inserted into Eq. (1) then SSD can be rewritten as Eq. (3):
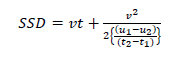 |
(3) |
It is assumed in the paper that density was a resultant of speed and flow hence not directly affected by night rainfall. This implies that stopping sight distance reduction was fully the result of speed changes. Speed is a key component of stopping sight distance estimation, it has a negative linear relationship with density. The introduction of a dummy variable into the speed/density linear equation indicates the presence or absence of night rainfall.
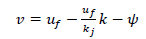 |
(4) |
Where; v ~ speed,
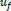 ~ free-flow speed, k ~ density, kj ~ jam density,
~ free-flow speed, k ~ density, kj ~ jam density,
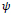 ~ (1 rainfall, or 0 ~ dry weather)
~ (1 rainfall, or 0 ~ dry weather)
If Eq. (4) is now plugged into Eq. (3), stopping sight distance equation can be rewritten as Eq. (5);
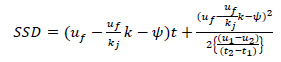 |
(5) |
Chu and Fwa [15] presented a new procedure for the determination of rain-related wet-weather VSLs as a function of water film thickness based on stopping sight distance criterion and minimum skid resistance. Bearing in mind that tyre-pavement friction coefficient u on a wet pavement varies with vehicle speed they argued that for rain-related wet-weather VSL determination, the actual deceleration that can be provided by the wet pavement can be determined with the expression Eqs. (6, 7):
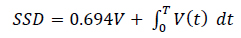 |
(6) |
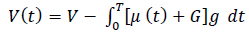 |
(7) |
Where SSD denotes stopping sight distance; V is initial speed at time zero expunge when the brakes are applied; T is total duration of braking time taken by the vehicle to come to a complete stop; V(t) speed at any time t, 0 ≤ t ≤ T; and is tyre pavement friction coefficient at time t when the vehicle speed is at V(t). Therefore, the calculation of stopping distance requires the establishment of the relationship between friction coefficient and vehicle speed.
3. MATERIALS AND METHODS
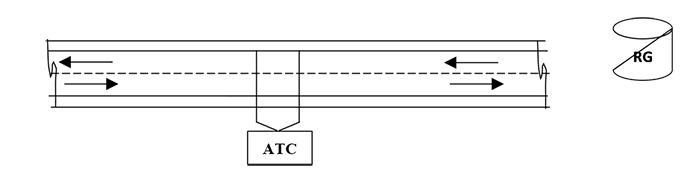
In the ‘with and without’ night rainfall empirical study at four selected sites, the main criteria for selection were; proximity of Rain Gauge (RG) station to the study site; absence of road light, and the road section must be flat and straight, devoid of pavement distress; devoid of attractions like a petrol station, rest area, billboards, and roadside parking sections, and must have functional drainage. Rainfall and traffic data were collected simultaneously and continuously for eight weeks. Over 500,000 sample vehicles were recorded. As shown below in Fig. (1), traffic data were collected using Automatic Traffic Counters (ATC) set at 100m apart. Rainfall intensities were classified as light rain (< 2.5mm/h); moderate rain (2.5mm/h and 10mm/h); heavy rain (10mm/h and 50mm/h).
Passenger Car Equivalent values (PCE) can be defined as the ratio of the mean lagging headway of a subject vehicle divided by the mean lagging headway of the basic passenger car. Lagging headway is defined as the time or space from the rear of the leading vehicle to the rear of the vehicle of interest; it is composed of the length of the subject vehicle and the inter-vehicular gap. The Passenger Car Equivalent values (PCE) initially used in the analysis were those specified by the Federal Ministry of Works (FMW) which were estimated under normal dry daylight conditions. There is a need to ascertain if they are suitable for rainfall conditions even though it was not the central focus of this study. A simplistic PCEs method of calculating based on headway was explored. However, the determination of passenger car equivalent values remains a subject of debate due to differences in estimation methods. The headway method is simple. It is the ratio of average headway of target vehicle to the average headway of the car. It is expressed as Eq. (8);
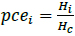 |
(8) |
Where; PCEi - passenger car equivalent of vehicle class i
Hi - average headway of vehicle class i (s) and
Hc - average headway of passenger car (s)
According to Ben-Edigbe et al. [4], headway values greater than 5 seconds are not significantly affected by rain hence vehicles with headways greater than 5s in this paper were filtered out while the remaining headways were used in PCE modification procedures. For example, where density is 20veh/km the pce modification procedure is presented as Eqs. (9, 10);
 |
(9) |
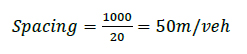 |
(10) |
Average speeds of identified vehicles class were considered
Average speed of passenger cars, PC = 82.37km/hr = 22.88m/s
Average speed of medium vehicles, MV = 78.44km/hr = 21.79m/s
Average speed of heavy vehicles, HV = 71.37km/hr = 19.83m/s
Thereafter, the average headway of each vehicle class was calculated using eq.(11)
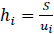 |
(11) |
Where hi= average headway of vehicle class i and S = spacing and = speed of vehicle class i
Headway for passenger cars, PC = 50/22.88=2.19s
Headway for medium vehicles, MV = 50/21.79=2.29s
Headway for heavy vehicles, HV = 50/19.83=2.52s
Modified PCEs were estimated using Eq. (11), for e.g.
PCE for passenger cars, PC = 2.19/2.19=1.00
PCE for medium vehicles, MV = 2.29/2.19=1.02
PCE for heavy vehicles, HV = 2.52/2.19=1.15
The procedures were repeated for other conditions and summarized below in Table 1.
From Table 1, it is evident that modified PCE values for medium and heavy vehicles are not the same as those specified in FMW manual. The change in PCE values is a result of traffic conditions under different weather conditions in which impaired visibility is a major factor. The PCE values for medium vehicles under night rain conditions increased though without a pattern as against its corresponding value for dry night-time conditions. However, for a heavy vehicle, the PCE values only changed under heavy night rainfall conditions. A statistical test using chi-square was performed where;
- Null hypothesis (HO): No difference between modified and FMW PCE values
- Alternate hypothesis (H1): There is a difference between modified PCE and FMWH values
Chi-square test was carried out at a 95 percent level of confidence for one degree of freedom where X2 = 3.84 as taken from the chi-square distribution table. If calculated chi-square X2 < 3.84, it means is no significant difference between the PCE variables, hence the null hypothesis (HO) is accepted, X2 > 3.84, alternate hypothesis (H1) is accepted, that is, there is a significant difference between the PCE variables. For example, Eq. (12)
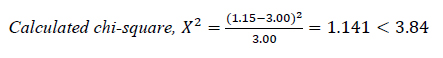 |
(12) |
In all cases, the null hypothesis (HO) was accepted because calculated chi-square, Xcal. < 3.84 and alternate hypothesis (H1) rejected. Since there is no significant difference, either FMW PCE or modified PCE could be used. For this study, preference is given to the modified PCE values since it reflects the prevailing condition of the study.
4. RESULTS AND DISCUSSION
Traffic volume was converted to traffic flow with modified passenger car equivalent values. Traffic flow was related to speed to derive density, suggesting that density was not directly affected by rainfall. A dummy variable (
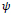 ) was introduced into the linear regression model such that
) was introduced into the linear regression model such that
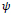 = 0 for dry night conditions and (
= 0 for dry night conditions and (
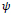 ) = 1 for rainy night conditions. The ensuing model equations shown in Table 2 were tested statistically and found fit. From the model equation, free-flow speed is 92.31km/hr for the dry night, while the free-flow speed for light rainfall is 92.31km/h - 8.58km/h = 83.73km/h. The standard deviation is estimated at ±10%.
) = 1 for rainy night conditions. The ensuing model equations shown in Table 2 were tested statistically and found fit. From the model equation, free-flow speed is 92.31km/hr for the dry night, while the free-flow speed for light rainfall is 92.31km/h - 8.58km/h = 83.73km/h. The standard deviation is estimated at ±10%.
For example, at site 01 Eq. (13):
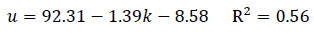 |
(13) |
As shown above, in Table 3, deceleration was estimated from equation 2 for example at site 01 eq.(14)
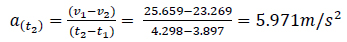 |
(14) |
From Table 3, the average deceleration induced by light rainfall is 6.29m/s2, moderate rainfall 5.95m/s2, and heavy rainfall 5.94m/s2. Chi-square results show that there is no significant deceleration difference. , it can be mentioned that the generalised average deceleration is 6.1m/s2 suggesting that acceleration is, in fact, 0.622g where g is 9.8m/s2. Road friction even though is a piece of important information for vehicle active braking control systems, estimating tyre/road friction accurately is not easy and not needed in this paper. Friction factor limits are 0 and 1 and the median is 0.5, therefore it can be postulated that deceleration values between 0.4g and 0.6g are acceptable for wet pavements given the empirical free-flow speeds in Table 3. In any case, the accuracy of friction in this paper is limited to its relationship with deceleration and gravitational force. It can be mentioned that wet road surfaces irrespective of intensity can be called to account partly for deceleration. Given that drivers will reduce approach speed instinctively if visibility is blurred irrespective of how it happened and that predicted free-flow speed is usually higher than empirical speed. The estimated decelerations were used to compute SSD for dry weather and night rainy conditions, as summarized in Table 3. As shown in previous studies, reaction times vary greatly between about 1.5s to 3s or more; some accident reconstruction specialists use 1.5s. Since human characteristics are dynamic, the estimation of reaction time need not be fixed, however, an assumption of a fixed reaction is permissible. A reaction time of 2s is used in this paper. From Table 3, SSD values for dry weather are higher than the ones from night rainy conditions partly because of speed differentials; dry weather speeds are higher than rainy weather speeds. Since the reaction time of 2s is applied to dry and rainy conditions, no scenario has an advantage that would alter the SSD outcome. Even if the lower reaction time is used, the resultant would be lower perception distance. Average SSD decrease attributed to light rainfall is 15.2m (14%), moderate rainfall 18.3m (16.8%), and heavy rainfall 21.2m (19.2%). The chi-squared test is used to determine whether there is a significant difference between the dry weather SSD and variable wet weather SSD at a 5% level of significance. For light rainfall, calculated X2 value of 2.42 < 3.14 tabulated X2 value, therefore, the observed frequency is not significantly different from the expected frequency. In other words, light rainfall has not changed the SSD significantly. For moderate rainfall, calculated X2 value of 3.6 > 3.14 tabulated X2 value, therefore, the observed frequency is significantly different from the expected frequency. In other words, moderate rainfall has changed the SSD significantly. For heavy rainfall, calculated X2 value of 4.96 > 3.14 tabulated X2 value, therefore, the observed frequency is significantly different from the expected frequency. In other words, heavy rainfall has changed the SSD significantly (Table 4).
| Vehicle Type | FMW | Modified PCE Values | |||
| Dry | Light Rain | Moderate Rain | Heavy Rain | ||
| Passenger car | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Medium vehicles | 1.75 | 1.02 | 1.05 | 1.03 | 1.04 |
| Heavy vehicle | 3.00 | 1.15 | 1.15 | 1.15 | 1.17 |
| Site | Rainfall | Model Equations | Free-flow speed (uf) | |||
| Dry Weather | Rainfall | |||||
| km/h | m/s | km/h | m/s | |||
| Light | 92.31 - 1.39k - 8.6 | 92.3 | 25.659 | 83.7 | 23.269 | |
| 01 | Moderate | 91.79 - 1.36k - 9.0 | 91.8 | 25.520 | 82.8 | 23.018 |
| Heavy | 92.67 - 1.28k - 7.6 | 92.7 | 25.771 | 83.1 | 23.102 | |
| Light | 93.81 - 1.59k - 8.2 | 93.8 | 26.076 | 84.6 | 23.797 | |
| 02 | Moderate | 90.66 - 1.35k - 12.7 | 90.7 | 25.215 | 78.0 | 21.684 |
| Heavy | 97.12 - 1.09k - 16.8 | 97.1 | 26.994 | 80.3 | 22.323 | |
| Light | 92.92 - 2.10k - 4.5 | 92.9 | 25.826 | 88.4 | 23.463 | |
| 03 | Moderate | 91.51 - 1.97k - 8.5 | 91.5 | 25.437 | 83.0 | 23.074 |
| Heavy | 90.66 - 1.89k - 10.3 | 90.7 | 25.215 | 80.4 | 22.351 | |
| Light | 100.5 - 2.17k - 11.2 | 100.5 | 27.939 | 89.3 | 24.825 | |
| 04 | Moderate | 98.91 - 1.68k - 12.8 | 98.9 | 27.494 | 86.1 | 23.936 |
| Heavy | 96.09 - 1.44k - 13.3 | 96.1 | 26.716 | 82.8 | 23.018 | |
| Site | Dry Weather | Rainfall | ∆ m/s |
∆ time |
a m/s2 |
|||||
| Speed km/h |
Speed m/s | Time (s) | Intensity | Speed km/h |
Speed m/s | Time (s) |
||||
| 01 | 92.3 | 25.659 | 3.897 | Light | 83.7 | 23.269 | 4.298 | 2.391 | 0.400 | 5.971 |
| 02 | 93.8 | 26.076 | 3.835 | 85.6 | 23.797 | 4.202 | 2.280 | 0.367 | 6.205 | |
| 03 | 92.9 | 25.826 | 3.872 | 84.4 | 23.463 | 4.262 | 2.363 | 0.390 | 6.060 | |
| 04 | 100.5 | 27.939 | 3.579 | 89.3 | 24.825 | 4.028 | 3.114 | 0.449 | 6.936 | |
| 01 | 91.8 | 25.520 | 3.918 | Moderate | 82.8 | 23.018 | 4.344 | 2.502 | 0.426 | 5.874 |
| 02 | 90.7 | 25.215 | 3.966 | 78.0 | 21.684 | 4.612 | 3.531 | 0.646 | 5.468 | |
| 03 | 91.5 | 25.437 | 3.931 | 83.0 | 23.074 | 4.334 | 2.363 | 0.403 | 5.869 | |
| 04 | 98.9 | 27.494 | 3.637 | 86.1 | 23.936 | 4.178 | 3.558 | 0.541 | 6.581 | |
| 01 | 92.7 | 25.771 | 3.880 | Heavy | 83.1 | 23.102 | 4.329 | 2.669 | 0.448 | 5.953 |
| 02 | 97.1 | 26.994 | 3.705 | 80.3 | 22.323 | 4.480 | 4.670 | 0.775 | 6.026 | |
| 03 | 90.7 | 25.215 | 3.966 | 80.4 | 22.351 | 4.474 | 2.863 | 0.508 | 5.636 | |
| 04 | 96.1 | 26.716 | 3.743 | 82.8 | 23.018 | 4.344 | 3.697 | 0.601 | 6.150 | |
| Site | Dry Weather | Rainfall | ∆ SSD (m) |
SSD ∆ % |
|||||
| Perception (m) |
Braking (m) | SSD (m) | Intensity | Perception (m) |
Braking (m) | SSD (m) | |||
| 01 | 51.32 | 55.14 | 106.46 | Light | 46.54 | 45.34 | 91.88 | 14.58 | 13.7 |
| 02 | 52.15 | 54.79 | 106.94 | 47.59 | 45.63 | 93.22 | 13.72 | 12.8 | |
| 03 | 51.65 | 55.04 | 106.69 | 46.93 | 45.42 | 92.35 | 14.34 | 13.4 | |
| 04 | 55.88 | 56.27 | 112.15 | 49.65 | 44.43 | 94.08 | 18.07 | 16.1 | |
| 01 | 51.04 | 55.44 | 106.48 | Moderate | 46.04 | 45.09 | 91.13 | 15.34 | 14.4 |
| 02 | 50.43 | 58.14 | 108.57 | 43.37 | 42.00 | 86.37 | 22.20 | 20.5 | |
| 03 | 50.87 | 55.12 | 105.99 | 46.15 | 45.35 | 91.50 | 14.49 | 13.7 | |
| 04 | 54.99 | 57.43 | 112.42 | 47.87 | 43.53 | 91.40 | 21.02 | 18.7 | |
| 01 | 51.54 | 55.78 | 107.32 | Heavy | 46.20 | 44.82 | 91.03 | 16.29 | 15.2 |
| 02 | 53.99 | 60.46 | 114.45 | 44.65 | 41.35 | 86.00 | 28.45 | 24.9 | |
| 03 | 50.43 | 56.40 | 106.83 | 44.70 | 44.32 | 89.02 | 17.81 | 16.7 | |
| 04 | 53.43 | 58.03 | 111.46 | 46.04 | 43.08 | 89.12 | 22.35 | 20.0 | |
CONCLUSION
This study is based on the hypothesis that the extent of stopping sight distance induced by night rainfall on dark roadways is significant. The aim behind this exercise is to establish the extent to which stopping distance can be sustained in the presence of night rainfall and the relationship between the two variables. To estimate stopping distance reaction time, free-flow speed, reaction distance and deceleration variables were used. Modified passenger car equivalent values were used to convert observed traffic volumes to flows. Regression techniques were used for the development of functions that relate free-flow speed to density. Based on the synthesis of evidences obtained from the relationship between night rainfall and stopping distance on dark roadways it is correct to conclude that on dark roadways; travel speed reduction will result from night rainfall, the value of reaction time can be fixed for ‘with and without’ rainfall scenarios, reaction/perception distance and braking distance decrease results from speed reduction, stopping sight distance decrease also results from speed reduction occasioned by night rainfall.
NOTATION LIST
| α | = Deceleration |
| ∆ | = Differential |
| ∆% | = Differential percentage |
| v | = Speed |
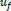 |
= Free-flow speed |
| k | = Density |
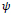 |
= Dummy (1 rainfall, or 0 ~ dry weather) |
| vt | = Perception / reaction distance |
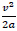 |
= Braking distance |
| t | = Reaction time |
| tn | = Reaction time fixed value for a certain driver n |
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
The authors confirm that the data supporting the findings of this research are available within the article.
FUNDING
This work was partially supported by the University of KwaZulu-Natal through a 3-year PhD Research Scholarship Granted to Makinde O.O.; Number 216073398 (2016-2019).
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The research team is grateful to all for their invaluable assistance at the data collection stage.


