All published articles of this journal are available on ScienceDirect.
Measuring the Reliability of Methods and Algorithms for Route Choice Set Generation: Empirical Evidence from a Survey in the Naples Metropolitan Area
Abstract
Background:
Route choice set definition is a very sensitive phase of the route choice simulation. Several heuristics, generally based on shortest path algorithm repetition, give as output choice sets that are very large, lading to questions about their behavioural consistency.
Objective:
This paper proposes a comparison of the main route choice set generation methods, contrasting the results of the commonly implemented heuristics with the revealed choice sets of a sample of employees and students moving within the Metropolitan Area of Naples.
Methods:
We described the data collection process and provided a statistical analysis of the sample data. In addition, since coverage measures and performance indicators, usually applied in the literature, do not take into account any possible biases related to the generated choice set cardinality. The current work proposes an analysis of the coverage of routes that are generated by the heuristics towards the revealed routes.
Results:
We observed that when the heuristics did not provide overlapped routes, although giving higher network coverage, they introduced a higher number of links not belonging to any observed route. In general, this may cause significant network loading errors. Therefore, the quality of a method for choice set generation should be measured as a function of the trade-off amongst network coverage and network loading bias due to excessive cardinality of the generated choice-sets.
Conclusion:
We found the randomization method, which is also less computational demanding, provided the best trade-off amongst network coverage and network loading bias
1. INTRODUCTION
Route choice models represent the core of the standard traffic assignment procedures. Notably, route choice simulation requires (i) the definition of the choice set and (ii) the application of a discrete choice model. Although (ii) has received a lot of attention within the literature, maybe (i) represents the most sensitive phase to deal with. Many researchers argued about the reliability of the choice set generation algorithms, in terms of behavioural consistency, for contexts wherein, in general, the total cardinality of the choice is very big [1-17].
Concerning the route choice, in particular, the literature identifies two main approaches for (i). The first one, namely the stochastic approach, aims at simulating the probability that an alternative belongs to the choice set. Theoretically, this could be done through one of the models proposed in the discrete choice theory for the choice set generation, either following the explicit approach [18-21], or the implicit approach, e.g the Implicit Availability Perception Logit IAP Logit [22]. In practice, only the latter approach has been applied in the route choice context and, to the author’s knowledge, only one study [23] tried to estimate the IAP Logit parameters on real data.
The second one, namely the deterministic approach, considers a pre-defined route choice set. According to such approach, several implicit or explicit enumeration routes procedures were proposed. The implicit enumeration procedures, although not explicitly considering the routes, allow loading the network in such a way that is consistent with some behavioural models. This way, they consider de facto, choice sets that are exhaustive with reference to (w.r.t.) some particular sets of links of the network. This means they consider all the routes that are composed of the links of some particular sub-sets of the network [24, 25] on the so-called efficient/reasonable routes) or of the whole network [26-33] on all feasible acyclic routes and even cyclic routes). However, a study [34] argued that implicit choice sets that are considered in the commonly implemented stochastic network loading procedures could be behaviourally unrealistic. Other authors proposed implicit enumeration procedures for dynamic traffic assignment (DTA; for applications in dynamic field [35-40] for instance). The exhaustive approach is unfeasible when dealing with simulation methods for DTA, which therefore, requires a deterministic selective approach. This approach is also useful in the context of Advanced Traveller Information Systems (ATIS) wherein, in order to provide drivers for en-route and pre-trip descriptive information, the selection of the routes, to which the information relates, does not represent a trivial issue. Providing reliable information to users en-route can be very useful in general for traffic management purposes, as discussed in a few studies [41-45]. Hence, an effective route choice set generation method may help in the design process of such information.
Explicit route enumeration techniques usually work with a selection of relevant alternatives (selective approach). Such approach has been recognized to be more realistic from a behavioural standpoint, because generally, respondents do not actually consider more than a few alternatives [46]. Moreover, explicit route enumeration procedures, different from the standard implicit enumeration procedures, can also account for non-additive impedances [47]. The selection of relevant alternatives, which are exogenously fixed in (i), is based on some heuristics. Such heuristics generally work with shortest path algorithms repetition (for a comprehensive review see [48]). Once (i) is completed, one of the existent route choice models can be applied for (ii). Examples of this are the simple Multinomial Logit [24, 25, 49], the C-Logit [50, 51], the Path-Size Logit [1, 5, 10, 52], the Multinomial Weibit [6, 53], the Path-Size Weibit [54, 55], the Cross Nested Logit [56-63], the Paired Combinatorial Logit [64] the Network GEV [65], the Multinomial Probit [66], the Mixed Logit [67, 68], the Combination of Nested Logit [69-72]. Such models can be endogenously or exogenously embedded into microscopic analytical traffic models [44, 73].
The remainder of the paper is organized as follows: Section 2 recalls the characteristics of the main route choice set generation approaches, with particular emphasis to methods that are tested in the paper; Section 3 reports a statistical analysis on the collected data; Section 4 presents the comparison methodology and the detailed results; Section 5 draws the main findings of the experimental campaign.
2. ROUTE CHOICE SETS HEURISTICS - THE MAIN APPROACHES
As underlined in the introduction, a number of deterministic methods for route choice set generation have been proposed in the literature. We identified three main approaches: (a) labelling approach [74], (b) k-generalization of the labelling approach (c) other heuristics complying other constraints (e.g., simple or double efficiency, maximum detour relative to the shortest path and so forth). In the following, we briefly underlined some theoretical and operational aspects of the above-mentioned approaches.
The labelling approach is based on the search for routes that are the best (minimum/maximum) according to some specified labelling criteria. As described in a study [74], each labelling criterion is usually applied in practice by changing the link impedances that the algorithm considers. Obviously, such practice represents only a proxy for simulating the selected labelling criteria.
The extension of the labelling approach to k-shortest paths can be addressed both in an exact and in an approximate way. In the exact case, the Lawler’s algorithm [75] provided the best solution. Surprisingly, such algorithm has not been applied frequently within the transportation literature, because researchers generally prefer some generalizations of the shortest path algorithms (see for instance [76]). This leads to two main issues: 1) the loop-less condition must be explicitly checked, 2) the memory requirement is very large, because label nodes should be stored in k-length lists. In short, the Lawler’s algorithm is based on a recursive partition of the exhaustive set of the network acyclic routes (for each o-d pair) in mutually exclusive subsets. At each step, the algorithm expands the shortest paths list by adding the shortest of them within each of the “active” partitions at that step. Notably, this approach ensures that a) only loop-less routes are taken into account and b) there is no need for storing k-length lists. The partitioning technique represents the key issue of such procedures, because it is based on adding/elimination rules applied to the shortest path links within the set to be partitioned. A study [77] reported a detailed analysis, some examples, and a study of the computational efforts of such procedure.
In the approximate case, the k-shortest path heuristic can be applied under three main approaches. The first two share the idea of modifying the network after the shortest path algorithm application. In more detail, the link elimination approach [78] deletes from the network, one at a time, all the links belonging to the shortest path on a given o-d pair, then searching for the shortest path within the new network, while the link penalty approaches [79], analogously, works on increasing the impedance of the links belonging to the shortest path. The third approach, namely the randomization or simulation approach, is based on drawing link impedances from prior assumed distributions (Normal, truncated-Normal, lognormal, gamma), with a shortest path algorithm repetition at each link impedance draws. A study [77] describes an efficient version that is based on a proper choice of the variance of the randomly drawn impedances. In practice, the rationale of this approach is the same underlying the Monte Carlo technique applied to the Multinomial Probit based assignment procedure (in which link impedances are drawn from mono-variate Normal distributions, considering variances proportional to the means).
When dealing with other heuristics, the algorithm to be adopted depends on the chosen method. Notably, it is quite easy to take into account Dial’s efficiency, as summarized, for instance, in a study [80]. Interestingly, a generalization of the Lawler’s algorithm can be applied for finding the k-constrained shortest paths following a given criterion. The generalization consists of introducing some links feasibility conditions in the partitioning phase and successively excluding all the partitions not meeting those requirements. In more detail, while all the routes of an unfeasible partition are, in turn, not feasible, the routes belonging to a feasible partition may be either feasible or not. For large k, imposing particularly restrictive constraints may lead to strong computational efforts. Notably, this algorithm allows handling the class of so-called “recursive route constraints”, i.e. the evaluation of link feasibility is conditional on the earlier links in the route. A branch & bound algorithm was proposed in a study [3] for finding a set of routes contemporarily satisfying a set of criteria. Such algorithm requires the whole exploration of all the feasible routes of the network. Moreover, the list of the routes that are generated by the algorithm is not sorted, in the sense that stopping the algorithm does not assure that the k routes determined up to that point are exactly the first k satisfying a criterion.
While the reliability of the route choice models has received attention within the literature [81], it is interesting to note there are only a few studies in the literature proposing a validation of the route choice set generation methods. Some authors [82] tried to validate choice set generation methods on aggregate data. They carried out a comparison among the observed link flows and assignment link flows deriving from the generated route choice sets. However, this procedure is too approximated for a detailed exploration of the choice set generation methods reliability. A comparison based on observed disaggregated data, both in terms of chosen routes and in terms of considered choice sets, should be more proper.
The main aspects influencing the quality and characteristics of the data, therefore influencing the validation, are the network characteristics (size, structure, density), the choice context (urban or inter-urban), and the data collection method (i.e. direct survey vs. GPS-based data). For this aim, the following section describes the collected dataset and proposes some statistical considerations on the observed data.
3. SURVEY AND DATA ANALYSIS
3.1. Network Topology
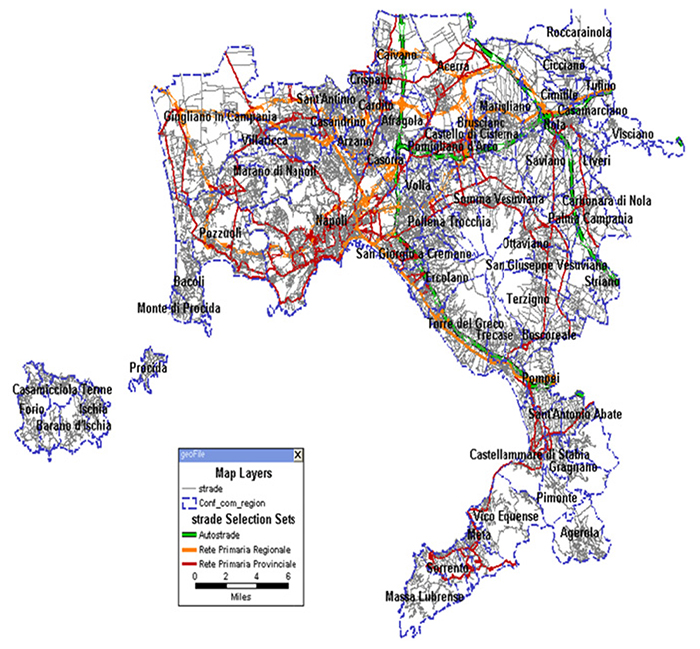
We contrasted the above-mentioned choice set generation methods based on data from a Revealed Preference (RP) survey. We proposed the survey to users of the metropolitan area of Naples (Italy). A complex and dense transportation network characterizes such areas. In more detail, the context can be classified as urban, but with a significant number of motorway connections between the downtown and the suburbs. The network is represented by a large-scale graph, made up of 53’938 nodes and 115’495 links, and is depicted in Fig. (1). 10.91% of the links represent motorway connections. We also compared the network characteristics with already available data (free-flow and critical speeds).
3.2. Data Collection
We collected the data through internet-based interviews, with the aid of interactive maps (Fig. 2). Each respondent was asked to track its route on the interactive map. This allowed also to avoid measure biases due to indirect detection (e.g. map-matching of GPS trajectories).
Furthermore, respondents were asked several questions, whose results will be mainly showed into Section 3.3, 3.4, and 3.5.
3.3. Sample Socio-demographic Data
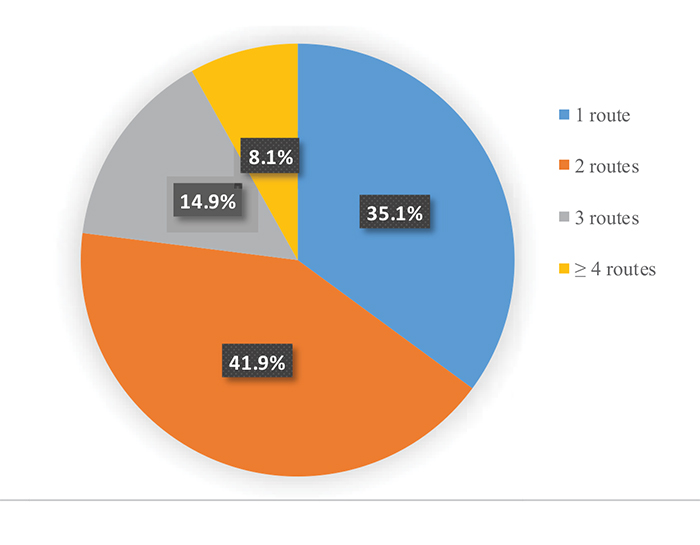
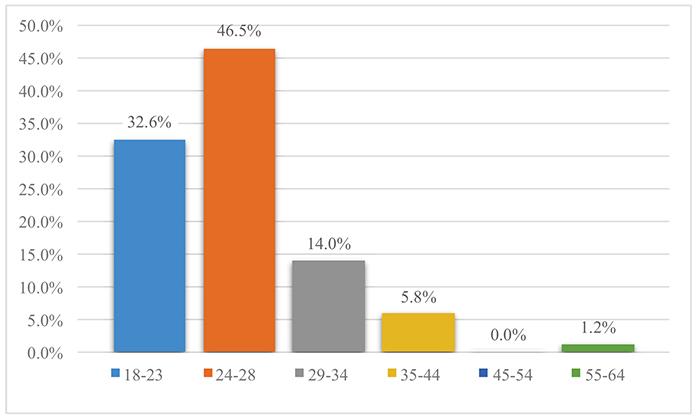
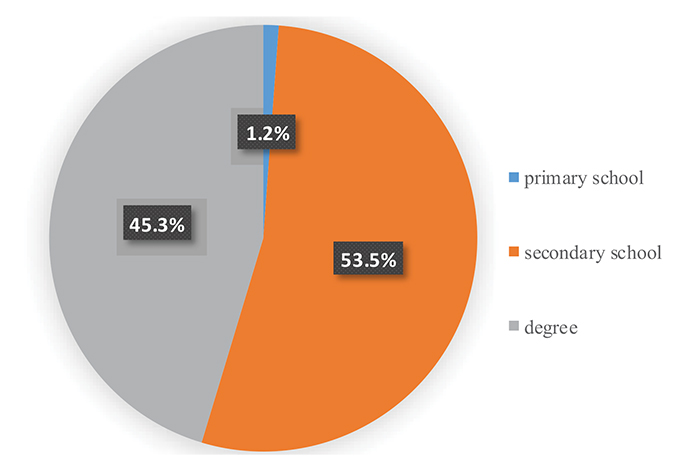
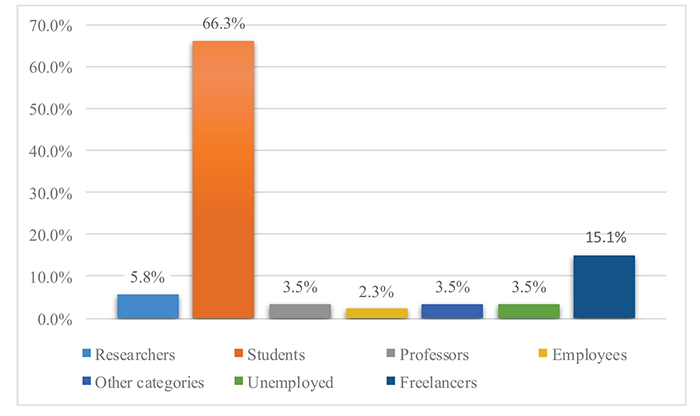
We recorded observations related to 186 o-d pairs for a total of 308 observed routes. In terms of interesting o-d pairs, we observed balanced shares of trips within the city of Naples and trips from/to Naples and its suburbs. In the first phase, we proposed the survey to employees and students of the Faculty of Engineering of the University of Naples Federico II. We asked each respondent to provide information about his/her commuting routes as well as other routes corresponding to trips classified as habitual. In more detail, we asked each one of them to provide the set of routes currently chosen, together with their corresponding choice frequency, for all o-d pairs corresponding to each habitual trip. Concerning choice set composition, we found the shares reported into Fig. (3), which shows that the most of the respondents (about 77%) actually consider only 1-2 routes. Figs. (4-6) depict age, education level, and employment shares characterizing the sample analyzed, respectively.
As can be seen from Figs. (4 and 6), the largest part of the analyzed sample refers to young individuals, particularly students. Almost the whole sample refers to the interval 18-44 years. Furthermore, students represent 2/3 of the sample. In particular, 80.2% of the analyzed sample were male respondents and 19.8% was female respondents.
3.4. Sample Routes Composition
It is also useful to explore the relative overlapping among the observed routes. For this aim, observed routes can be grouped according to their Path-Size (PS) attribute, defined as:
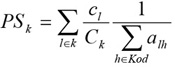 |
(1) |
Where, cl is the impedance of link l, Ck the impedance of route k and alh the generic 1/0 link-routes incidence matrix element, equals to 1 if lϵk, 0 otherwise. The Path-Size measure belongs to the [0,1] interval, and a value equal to 0 means that route is not overlapped with the others. The observed average PS value is 0.69, but it is worth remarking that the presence of o-d pairs characterized by the observation of a considerable amount of not overlapped routes influence such value. Typical examples of this occur when comparing a route, including the city bypass, with one passing inside the urban area.
In terms of network hierarchy, the routes are composed of motorway links for 37.4% of their total length. Moreover, the average length is 15,386 kilometers. The percentage of observed motorway links differ from the actual percentage of them in the network. This occurs because of the kind of observed o-d pairs, which refer to almost 50% of the trips to/from Naples, in which users normally travel on motorways. Interestingly, almost one-third of the observed routes are composed of percentages of motorway and urban links very close to each other, representing a significant test field for the choice set generation methods. Finally, about 40% of the observed routes do not exhibit a clear hierarchy of links (e.g. secondary links for access/egress to/from a motorway), thus we did not take into account hierarchical heuristics when choosing the route choice set generation methods.
3.5. Analysis of Perceived Route Characteristics
We asked the respondents to provide information about the importance they give to some relevant attributes, in particular: travel time, total length, toll, and geometry. They were asked to classify the importance according to 5 increasing levels. The results are shown in Fig. (7). As can be seen, travel time is perceived as a key aspect by 70% of the sample, and it represents the sole attribute that the respondents are very sensitive to in high percentage.

Different response has been provided for distance, toll and route geometry. However, they are classified at least as “considerable” (i.e. the intermediate level) by 75%, 61%, and 54%, respectively.
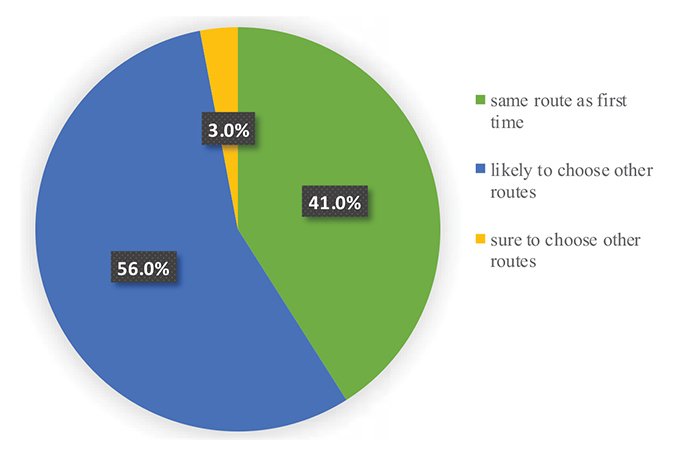
Fig. (8) shows another interesting aspect that relates the willingness to change routes. Most of the sample (56%) declares it would be likely to choose a different route if travelling a second time on the same o-d pair.
We also asked the respondents to provide information about the perceived characteristics of the observed routes, such as length, mean, minimum and maximum travel time. It is worth analyzing the distribution of the perception errors in those attributes, particularly for length, which represents a directly observable route attribute. Interestingly, the mean error in length perception is 1.68 kilometers (significantly different from zero at 95% confidence threshold), corresponding to a 12.78% percentage error. The same occurs for minimum time perception, which is overestimated as 4.61 minutes on average. Anyway, the perception errors variance is significantly greater for travel times than for lengths.
We carried out a statistical analysis in order to find possible relationships among perception errors and specific routes characteristics. In more detail, we found a significant negative correlation (equal to -0.126) between the length perception error (defined as declared length minus the actual one) and the percentage of urban links in the route. This means that drivers tend to systematically underestimate the length of urban links. Similarly, we observed a negative correlation (equal to -0.167) between time perception error and motorway links percentage in the routes, i.e. drivers tend to underestimate travel time for motorway links. Moreover, we observed a significant positive correlation (equal to 0.340) between length percentage overestimation and travel time. Finally, the mean percentage difference between the actual shortest path and the observed shortest path from the sample on each o-d pair is -23% and -18% for length and travel time, respectively. This means that the users systematically tend not to choose the shortest path, especially in terms of length.
4. MATERIALS AND METHODS
4.1. Choice Set Generation Methods and Algorithms
We considered the following route choice set generation methods for the comparison:
- k-shortest paths through Lawler’s algorithm;
- k-shortest paths through randomization. We assumed a variance corresponding to a coefficient of variation cv=0.30 as reference value;
- k-shortest efficient routes w.r.t. the sole origin, to the sole destination, and to both (doubly efficient). Those routes are obtainable applying Lawler’s algorithm to the subnetwork made up by the links satisfying the efficiency conditions;
- k-shortest detour constrained routes through the algorithm described in a study [77]. We fixed the detour thresholds, respectively, to 1.20 and 1.50;
- k-shortest paths with maximum overlap of 75%, through the algorithm described in a previous study [77].
We considered free-flow travel time and length as link impedances. Moreover, we set a maximum value of k=60 for each method that results in an upper bound to the cardinality of the considered routes for each o-d pair. It is worth underlining that we did not further explore the labelling approach (apart from travel time and length) because, as reported in previous studies [1] and [35], each labelling criterion (e.g. scenic links, number of left turns, traffic lights and so forth) is usually applied, in practice, by applying an opportune increase to link travel time, according to an estimated percentage. In practice, the effect of this heuristic is that of generating a choice set made up by routes with a small overlapping degree. Therefore, explicitly imposing an overlapping threshold can circumvent this issue, leading to similar results. As previously said, we did not consider generation methods based on hierarchical classifications of the links, which, however, may be easily introduced as particular constraints within the modified Lawler’s algorithm.
4.2. Indicators
Several indicators can be used for the target. Following the literature, the percentage coverage (%COVog) is one of the most relevant. It is defined as the percentage of observed routes that can be classified as “reproduced”. A route can be labelled as reproduced when there is at least one generated route that is overlapped with it beyond a certain threshold. The percentage coverage is defined as follows:
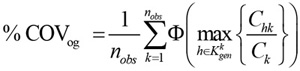 |
(2) |
where:
- nobs is the number of observed routes;
- Kkgen the set of generated routes for the o-d pair related to route k;
- Chk the overlap between h and k (measured w.r.t. a chosen link impedance);
- Ck is the impedance of the observed route k;
- Φ(∙) a 1/0 binary function that is equal to 1 if the term in brackets exceeds the fixed overlap threshold (chosen between 0 and 1), 0 otherwise.
Similarly [74], proposes the following consistency index as coverage indicator:
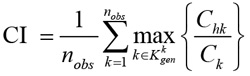 |
(3) |
which substantially provides the same information of the indicator (2).
The previous indicators measure to what extent the generated routes are able to reproduce the observed routes w.r.t. the specified threshold, but they do not provide information on the generated routes within Kkgen. The number and the characteristics of the generated routes should also be checked, in order to avoid significant biases in traffic assignment. For instance, a set Kkgen generated searching for routes maximizing the number of used links may provide a high coverage, accordingly to the above indicators, through unrealistic (i.e. unlikely to be chosen) routes. Therefore, the quality of a route choice set generation method cannot be entirely evaluated as a mere function of such coverage measures. With this premise, this paper aims at analysing the reliability of the methods and algorithms for route choice set generation, by evaluating the trade-off amongst coverage and network loading bias due to big cardinality of generated route choice sets.
However, different percentage coverage measures, which take into account also the impedance of each generated route h, can be considered in order to address this issue. For instance, the maximization of the coverage term 2Chk/(Ch+Ck), introduced by a study [82], without analysing the differences with the usual percentage coverage indicator, can be adopted. Different measures can also be introduced, e.g. by mimicking the structure of the commonality factor proposed by a previous study [50], by introducing into (2) the following term:
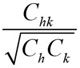 |
(4) |
Interestingly, when applied to the collected dataset, described in the previous section, those indicators were not able to clearly identify the magnitude of the bias underlying the set of routes generated with a given method. Therefore, we introduced a different approach. In more detail, we considered the same coverage indicators defined above w.r.t. the set of generated routes towards the set of observed routes (%COVgo), i.e. inverting the references to observed and generated routes in the formulae. The latter indicator, to the best of the authors’ knowledge, has not previously been used in route choice literature. This calculation allows directly checking whether a generated route is significantly different from the observed route that it should reproduce. Both %COVgo and %COVog can provide a more effective measure on how close the generated and observed route sets are to each other.
5. RESULTS AND DISCUSSION
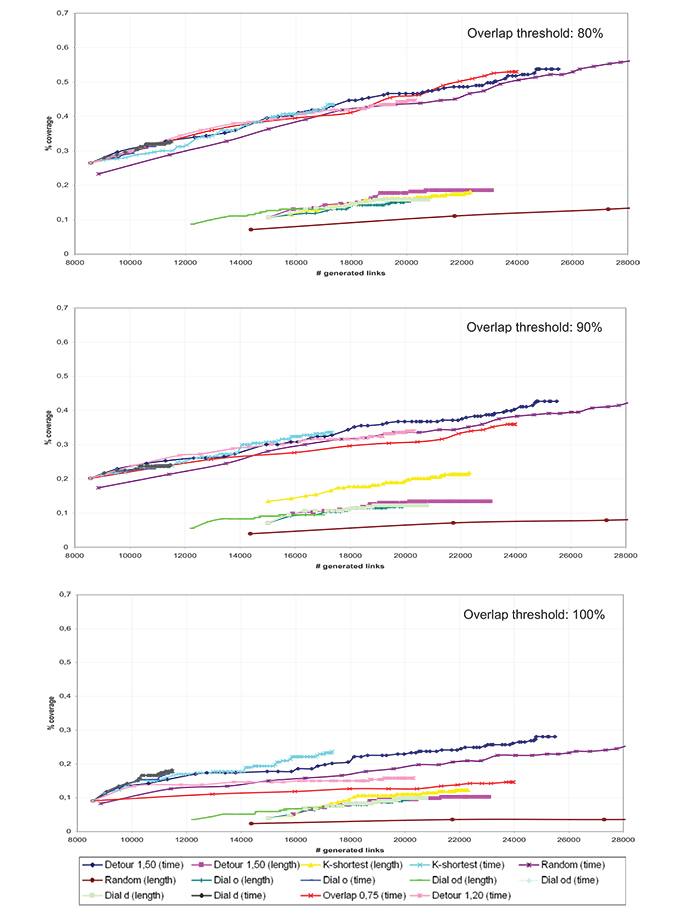
Fig. (9) reports the percentage coverage %COVog as a function of the number of generated routes, for three different overlap thresholds: 80%, 90%, and 100%. We indicated the methods in the legend following the labels reported in Table 1.
| Label | Description of k-shortest Path Method. |
|---|---|
| Detour 1,50 (length) | maximum detour of 50% w.r.t. the length of the minimum length path |
| Detour 1,50 (time) | maximum detour of 50% w.r.t. the total travel time of the minimum time path |
| Detour 1,20 (time) | maximum detour of 20% w.r.t. the length of the minimum length path |
| Overlap 0,75 (time) | by deleting routes that are overlapped more than 75% |
| k-shortest (length) | with Lawler's algorithm applied with links length as impedances |
| k-shortest (time) | with Lawler's algorithm applied with links time as impedances |
| Random (length) | with randomization method by drawing links length errors |
| Random (time) | with randomization method by drawing links travel time errors |
| Dial o (length) | with Lawler's algorithm applied with links length as input, considering only Dial efficient links w.r.t. o |
| Dial o (time) | with Lawler's algorithm applied with links time as input, considering only Dial efficient links w.r.t. o |
| Dial d (length) | with Lawler's algorithm applied with links length as input, considering only Dial efficient links w.r.t. d |
| Dial d (time) | with Lawler's algorithm applied with links time as input, considering only Dial efficient links w.r.t. d |
| Dial od (length) | with Lawler's algorithm applied with links length as input, considering only Dial efficient links w.r.t. od |
| Dial od (time) | with Lawler's algorithm applied with links time as input, considering only Dial efficient links w.r.t. od |
All the methods perform poorly when choosing the length as link impedance, leading to a coverage lower than 0.2, except for the randomization procedure. A similar result was found by two previous studies [1] and [50], while another study [3] found out a better coverage when applying the length rather than the free-flow time as link impedance. Since data revealed that drivers perceive length with a small error and the shortest path they declare is significantly longer than the shortest length, we concluded that other attributes affect their route choice behavior in heterogeneous networks. As evidenced in the literature, when the network is homogeneous (e.g. a completely extra-urban context) the length attribute is able to explain a significant percentage of drivers’ route choices. Therefore, attention will be focused in the following on free-flow time as link impedance.
Interestingly, the overlap constraint criterion outperforms the other methods, leading to a satisfactory coverage degree also for a small number of generated routes. Results also suggest that this happens when the overlap threshold and the overlap constraint are close to each other, e.g. a 75% overlap constraint provides good and poor coverage, respectively, for 80% and 100% overlap. The randomization criterion and detour constraint methods also provide good coverage. The latter improves its performances as the detour threshold decreases. Note that the effect of randomization and detour constraint methods is that of providing routes that are substantially not overlapped. This likely explains why their results are close to those of the overlapping constraint method. In addition, it suggests that looking for a significant network exploration, through the generation of not very overlapped routes, is the key issue to achieve good coverage.
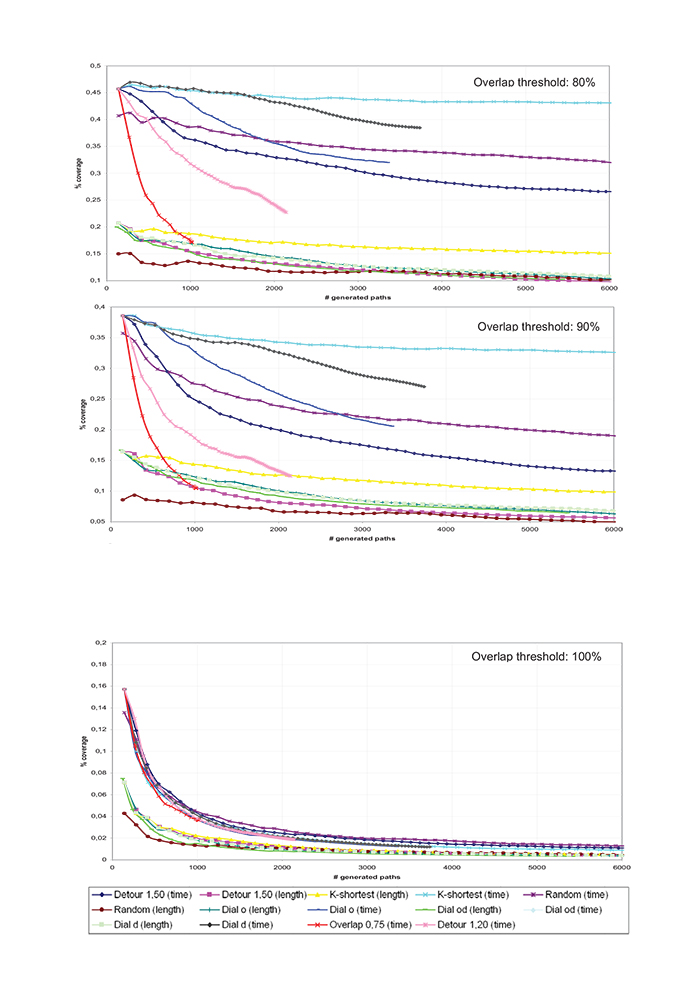
The diagrams in Fig. (2) support such results, reporting the percentage coverage %COVog as a function of the number of generated links (i.e. links included in the generated routes). All the methods exhibit a similar trend, at least for overlap thresholds lower than 100%.
We observed symmetric results when considering the percentage coverage %COVgo in Fig. (3). Specifically, the methods providing higher %COVog values through a larger network exploration exhibited a higher number of “biased” links, i.e. generated links not belonging to the set of observed routes, leading to poor %COVgo values. Remarkably, the randomization method shows a more robust behaviour w.r.t the detour constraint and overlap constraint methods.

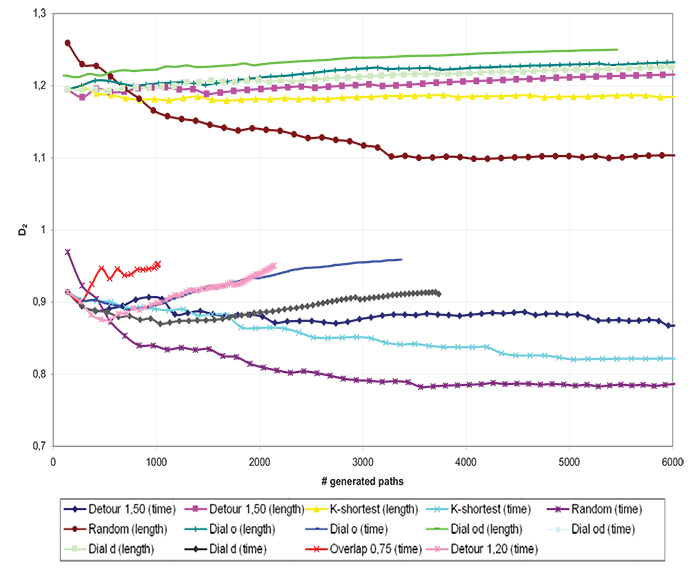
We found that %COVgo and %COVog measures can be combined in order to provide a synthetic indicator, e.g. the distance from the “ideal” route choice set generation algorithm. Such indicators represent an original contribution of this paper and is given by:
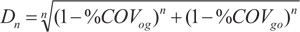 |
(5) |
The calculation of this indicator confirmed the greater stability of the randomization methods, for which the indicator (5) clearly decreases as the number of routes increases, as shown in Fig. (4). This confirms that, despite being considered as obsolete, the randomization method empirically best fits the actual choice-sets. Therefore, it is the more behaviourally consistent method on this dataset.
Some other analyses have also been carried out w.r.t. a single o-d pair. Generally, the route choice generation methods providing a higher coverage also exhibit better performances in covering each o-d pair. In more detail, the randomization approach gave a good coverage also for some critical o-d pairs, while the other methods provided poor performances. Substantially, the randomization method dominates most of other methods, and this is the reason why combining different methods does not offer a significant improvement in terms of coverage of the revealed routes.
CONCLUSION
This paper deals with a comparison of deterministic route choice set generation methods, based on a real dataset of observed route choices and revealed choice sets. We collected the data with the aid of computer-based surveys that we proposed to travellers (mainly students and University employees) of the metropolitan area of Naples. Such kind of computer-based interviews, performed with the aid of interactive maps, helped us to avoid biases due to map-matching of passively detected trajectories. A statistical analysis concerning several characteristics and preferences of the individuals of the sample has been carried out.
The proposed comparison starts with exploring the coverage of generated routes towards the observed routes. The main result is that exploring a significant part of the network, which directly derives from generating routes that are slightly overlapped, normally leads to a high coverage, but introducing, at the same time, a higher number of links not belonging to any revealed route. This may cause significant errors in terms of stochastic network loading. Therefore, the quality of a method for route choice set generation should be evaluated as a function of the trade-off among network coverage and network loading bias. Therefore, we evaluated the trade-off amongst coverage, which would require increasing the cardinality of the generated choice-set, and network loading bias, which would require reducing it. With this purpose, we proposed a new indicator, namely (5), as a trade-off measure. From this standpoint, the randomization method (which is also the less computational cumbersome), despite being considered as obsolete, provided the best results. This also suggests that the Probit model is the most reliable for route choice simulation because is inherently consistent with the best route choice set generation method.
We considered some results as quite general. For instance, the maximum number of considered routes in Fig. (3) confirms that individuals are hardly likely to consider more than 2-3 routes. The same applies to the importance of the attributes depicted in Fig. (7), which shows that travellers are primarily concerned with travel time.
According to these considerations, the results in (Figs. 9-10) appear quite general, because coverage is easily accommodated when the actual choice set cardinality is small. Conversely, the trade-off is ensured by opportunely limiting the number of generated routes, thus we expect no different trends on other samples than those of (Figs. 11-12). When analysing bigger samples, the analyst may increase the parameter k of the k-shortest paths algorithms. Furthermore, we compared choice set generation method by mainly considering travel time as link impedance, consistently with Fig. (7) results.
Other considerations made in the paper, instead, may be circumscribed to the analysed sample. For instance, it is expected that willingness to change routes and actual choice-set cardinality may be influenced by age and education levels that are different from those of the analysed sample. Higher age and lower levels of education may influence some factors. For instance, choice-set cardinality and willingness to change routes may be smaller. However, they would translate into a choice-set cardinality reduction and, according to the above considerations, this would represent a benefit for the main target of the paper.
CONSENT FOR PUBLICATION
All patients participated on a voluntary basis and gave their informed consent.
FUNDING
This study was funded by the Departments of Excellence for Civil, Construction and Engineering Environmental under grant no CUP E65D18000820006.
CONFLICT OF INTEREST
The author declares no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The authors wish to thank Donato Cavallaro for his precious cooperation in the data collection phase.


