All published articles of this journal are available on ScienceDirect.
Dynamic Flow Algorithm with Intermediate Storage for Emergency Evacuation Allowing Lane Reversal based on Incomplete Intuitionistic Fuzzy Preference Relation
Abstract
Background
Evacuation in case of disasters is of the greatest importance because of significant occurrences of natural and artificial disasters worldwide, which is why a reliable evacuation plan is always needed. However, evacuation models are difficult to develop due to various uncertain aspects that need to be considered, multiple and often conflicting criteria for evaluation and as lack of expertise regarding a specific preference of alternatives.
Objective
This study aims to transport the maximum number of evacuees in a dynamic network with lane reversal by a safe pattern of transportation, i.e., allowing storage at intermediate nodes. The optimal order of shelters and intermediate nodes for a reliable evacuation plan will be defined by incomplete intuitionistic fuzzy preference relation.
Methods
The illustrated method incorporates multiple and often conflicting criteria into a process of emergency decision-making. When evaluating evacuation alternatives, a decision-maker may hesitate and be unsure which alternative is better or not have sufficient expertise to evaluate a pair of alternatives. To model uncertainty and hesitation, intuitionistic fuzzy values are used to describe alternatives in more detail. This study relies on flow models and graph theory to simulate the movement of evacuees to safe destinations. Furthermore, fuzzy methods and their recent modifications are applied to determine the effective priority order of shelters. A case study which simulates the evacuation of aggrieved to safe destinations is presented.
Results
A method of evaluating the shelters and intermediate nodes for evacuation based on incomplete intuitionistic fuzzy preference relation is proposed. The method allows the missed values of experts’ assessments to be filled in regarding the evacuation alternatives and deals with intuitionistic fuzzy values, which describe experts’ hesitation. The dynamic character of flow distribution enables transit arc capacities and time factors to be processed. The contraflow technique, which is a powerful tool to decrease traffic jams and congestion on roads by reversing the movement along the unused segments, is applied to maximize the number of survivors.
Conclusion
The results of the method were compared to those of existing methods, and their consistency was proved. In the future, we intend to apply interval-valued intuitionistic preference relations and iterative algorithms to improve the consistency of intuitionistic preference relations to the tasks of transporting the maximum possible number of aggrieved to safe locations.
1. INTRODUCTION
1.1. Evacuation
Evacuation as a part of response to a hazardous situation caused by a natural or man-made emergency can save lives and property and alleviate the impact of disasters. The evacuation of endangered people, especially in urban areas, may be difficult. Therefore, planning and preparedness for threats is important to ensure an effective and successful evacuation. In case of an evacuation decision, the evacuation plan must be imple- mented and well-managed. Thus, preparedness and management of evacuation is subdivided into planning, decision-making, and implementation of the plan [1].
Among the most popular approaches to support evacuation preparedness and decision-making are:
- Forecasting and warning about the level of danger to analyze potential risks;
- Models and approaches to analyzing hazards in a specific location;
- Evacuation models to estimate evacuation time;
- Approaches to optimizing evacuation alternatives and evacuation paths;
- Decision-making criteria for assessing evacuation strategies;
- Geographic Information Systems (GIS) for determining location mapping and visualization of evacuation paths, shelters, evacuation maps, etc [1].
It is important to conduct an accurate analysis of evacuation decisions because mistakes may be costly. However, decision-makers, despite a thorough evaluation of the circumstances, are faced with multiple factors and uncertainties.
Evacuation support models are based on the premise that evacuation planning is partly disaster-specific, but the way evacuation is managed is relatively common across different types of hazards. Research into evacuation support models has been carried out in three areas: evacuation behavior models, traffic models, and critical path time models.
Evacuation traffic models are related to road traffic and consider the movement of aggrieved vehicles from a dangerous area to a safe location. During an evacuation, many vehicles must move along the network in a relatively short period of time. In urban areas, this is associated with a high risk of creating large congestion, which can affect the safety of evacuation.
Evacuation traffic models can be classified as follows:
- Macroscopic flow models based on optimization approaches in which the movement of vehicles is simulated as a homogeneous group forming a traffic flow [2]. Models allow optimal traffic to be built without considering the personal traits of the aggrieved;
- Agent-based models, in which individual vehicles are considered agents with autonomous behavior interacting with other vehicles [3];
- Simulation models based on scenarios for determining bottlenecks and estimation evacuation time [4].
The work [5] illustrates a literature survey regarding evacuation traffic.
In the present paper, a macroscopic evacuation model will be proposed, which presents aggrieved as a common system to remove people far from danger. In the model, the dangerous area is presented as a dynamic network whose nodes are shelters or rooms or road interseсtions while hazard areas represent sources and safe locations are sinks. Dynamic time-varying arcs show the connec- tions between roads, for example, road sections or railways. Arcs and nodes of the network have capacities that are bound to the upper limit of flow, which can enter this arc/node. Various approaches to evacuation planning based on flow models are presented in [6].
Previously, our research team has introduced fuzzy dynamic models whose parameters vary in time depending on the departure [7-9]. The study network in this paper is presented by a fuzzy dynamic graph. Rarely do existing methods of macroscopic evacuation consider the potential of intermediate nodes to store the flow. However, this factor should be incorporated into evacuation models as it allows for transporting more flow units to the safe destination. Owing to limited arc capacities, the desired amount of flow moved from the hazard destination may not reach the safe sink. In this regard, evacuation models allowing intermediate flow storage at nodes are of the greatest interest among researchers [10-13].
During the evacuation planning, decisions should be made regarding the order of evacuation alternatives. Decision-makers compare the shelters on the basis of various parameters and choose the preferable destinations first in order to make the process of evacuation smooth. The correct priority order of shelters and intermediate nodes influences the total number of those who escaped at each shelter. Literature review shows that existing methods of macroscopic evacuation based on the flow transmission consider distances from the endangered area to the safe one as the main factor that influences the order of shelters and intermediate nodes for evacuation [10-12].
However, distance, as the only factor for assessment, does not consider all the factors that influence the final decision. The safety of transportation, the resilience of the intermediate node, the level of reachability, and the hazards of the evacuation path should be taken into account. In our previous works, we proposed some mathematical models that considered various factors besides the distance from the hazard to find the order of nodes for evacuation [14-17].
1.2. Emergency Evacuation and Decision-making
Real emergency situations require instant reaction of decision-makers who should give their assessments affected by devastating environmental factors and uncertainty. While in emergency decision-making, a decision-maker provides his/her preferences by comparing the relation of each pair of alternatives under study. Preference relation as a tool of decision-making is widely used in various areas, for example, investment decision-making, supply chain management, and project prioritization [18]. However, this approach is not ubiquitous in emergency decision-making despite its effectiveness. Some research into emergency decision-making was conducted in a previous study [19-21] in order to prioritize evacuation alternatives.
Emergency decision-making tackles the impreciseness of decision data, inaccuracies, and lack of necessary knowledge. Some parameters of evacuation networks can be missed or assessed in qualitative form only, which is why fuzzy logic, as a powerful tool to handle uncertainty and vagueness, can be effectively used in emergency decision-making. Methods based on statistics and numerical approaches require numerous experiments to be well-calibrated. Deterministic methods and optimi- zation approaches may provide admissible results for finite-dimensional problems but do not consider uncertai- nties. Therefore, fuzzy logic dealing with subjective uncertainty is more effective than applying deterministic, probabilistic, or heuristic approaches. Furthermore, fuzzy set theory allows the inclusion of non-quantifiable data, incomplete and inaccessible information, and overlooked facts into the decision-making model. Consequently, fuzzy approaches appear to be especially suitable for making evacuation decisions when data are scarce, knowledge of cause-and-effect relationships is imprecise, and obser- vations and criteria can be expressed in linguistic qualitative terms [22]. In a previous study [23], it was suggested that the best places to build nuclear power plants in Indonesia be ranked based on 21 different criteria. For this purpose, two fuzzy algorithms (Chang’s Extent Analysis and Buckley’s Fuzzy Analytical Hierarchy Process (AHP) were applied to find the priorities of criteria as well as the Nuclear Power Plant (NPP) site feasibility of two locations in Indonesia. Ashraf et al. [24] considered the case of the Tianjin Port fire and explosion tragedy to put the on-site rescue plan on hold. They asked for an emergency decision-making to be developed in response to the emergency based on a Complex Probabi- listic Hesitant Fuzzy Soft Set, which was represented by a membership in 2-D with hesitant probability. Chen and Luo in a previous study [25], proposed a hybrid emergency decision-making method by combining best andthe worst method, multi-attributive border approximation area comparison, and prospect theory in trapezoidal interval type-2 fuzzy rough environment for site selection of makeshift hospitals in Wuhan. A previous study [26] presented a multi-granularity proportional hesitant linguistic TODIM (an acronym for interactive and multi-criteria decision-making in Portuguese) method in a mine emergency decision-making to select the best emergency alternative in case of the gas explosion that occurred in Linfen, Shanxi Province. In another study [27], an extended TODIM method based on bidirectional projection was proposed to solve the emergency group decision-making problem in the context of hesitant triangular fuzzy sets to define the effective strategy during COVID-19.
1.3. Multi-attribute Decision-making
A decision-maker may face problems in providing the assessments of alternatives due to both an insufficient level of knowledge and difficulties in establishing prefer- ences regarding attributes. These factors provide some level of experts’ hesitation. The evaluations of alter- natives may be imprecise or expressed with a specific degree of certainty. Therefore, experts’ preferences can be presented as fuzzy numbers rather than crisp numbers, such as intuitionistic fuzzy numbers. In this regard, we perform fuzzy preference decision-making to evaluate the evacuation alternatives as nodes for evacuation that may store the flow, which allows us to make evacuation decisions more comprehensively and effectively.
Due to the decreasingly difficult evacuation environ- ment, when considering many aspects of decision-making needed, involving the expertise and knowledge of several decision-makers is recommended, each of whom is an expert in his/her field. In this regard, group decision-making is a powerful tool for making reasonable decisions, which can be applied to the tasks of emergency eva- cuation, such as ranking the shelters and intermediate nodes with storage for further evacuation.
A comparative analysis of fuzzy optimization methods for solving problems of multicriteria and group decision-making in fuzzy conditions was carried out. The most common fuzzy methods for multicriteria optimization are the fuzzy methods ÉLimination Et Choix Traduisant la REalité (ELECTRE), The Preference Ranking Organization Method for Enrichment of Evaluations (PROMETHEE), Višekriterijumsko kompromisno rangiranje (VIKOR), Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), AHP, Analytic network process (ANP) and Decision-Making Trial and Evaluation Laboratory (DEMATEL). The citations of the ELECTRE fuzzy method in the Scopus database contain over 1100 publications on several subject areas. The most cited article devoted to a fuzzy ELECTRE method is the work of Bender and Simonovic [28]. The most cited research into the fuzzy PROMETHEE method is the study of Goumas and Lygerou [29]. The number of articles indexed in Scopus and devoted to fuzzy VIKOR includes over 900 publications in various subject areas, and the most cited paper is the study by Sanayei et al. [30]. The number of articles indexed in Scopus and devoted to fuzzy TOPSIS includes over 4000 publications in various subject areas. Among the most cited studies on fuzzy TOPSIS is the study of Boran et al. [31]. The most cited article on the AHP method is [32] and according to the ANP method [33]. DEMATEL is one of the most effective tools for determining cause-and-effect relationships between decision assessment criteria. The literature on the fuzzy DEMATEL method based on the SCOPUS database includes about 600 publications, and the most cited is the article by Wu and Lee [34].
1.4. Preference Relations
The literature survey provides several types of preference relations: multiplicative preference relations, fuzzy preference relations, linguistic preference relations, hesitant preference relations, and intuitionistic preference relations. The first four types were extensively discussed in the literature [35-37], whereas the latter received less attention because it was introduced later than previously. However, intuitionistic preference relation may be an effective tool to cope with imprecision, fuzziness, lack of data, experts’ hesitation, and linguistic type of data [38-40]. Intuitionistic preference relation was considered by Szmidt and Kacprzyk [40] as a preference matrix and a matrix of intuitionistic fuzzy indices. Later. Xu [39] introduced a definition of intuitionistic preference relation motivated by the concept of an intuitionistic fuzzy set of Atanassov [41] because of its practical applications. This relation consists of elements such as intuitionistic fuzzy values. The first is the certainty degree, which reflects the degree to which the alternative ai is preferred to the alternative aj; the second is the certainty degree, which shows the degree to which the alternative ai is non-preferred to the alternative aj, and the third is the indeter- minacy degree which illustrates the level of the decision-maker’s hesitation regarding the preferences. Xu [42] proposed consistent intuitionistic fuzzy preferences based on additive transitivity and multiplicative transitivity. to solve the domestic appliance selection problems. Xu and Yager [43] proposed a consensus-reaching procedure for group opinions. Further directions of research were devoted to improving the consistency of all individual intuitionistic preference relations [44] and developing intuitionistic aggregating operators Zhao and Xu [45]. The tasks of emergency decision-making based on preference relation were considered in the literature as well. For example, Zhang et al. [46] considered multiplicative linguistic preference relations where individual assess- ments of decision-makers were adaptively adjusted based on fuzzy granulation optimization of multiplicative linguistic preferences to assess five emergency alter- natives for liquid ammonia leak in China. In a previous study [47], incomplete, hesitant, fuzzy linguistic preference relations were illustrated for mine disaster rescue plans in China by evaluating four emergency alternatives. Gao et al. [48] introduced incomplete probabilistic linguistic preference relations based on a hesitant fuzzy linguistic element to choose an ideal response action to manage college infectious disease to rate four emergency responses. A knowledge-unit-based case-based reasoning method to generate the optimal emergency alternative in case of typhoon emergency based on linguistic intuitionistic fuzzy preference relations (LIFPRs) was proposed by Zhang et al. in [49]. Wu et al. [50] used a hesitant multiplicative linguistic preference relation for the selection of suitable sites for earthquake shelters, which not only incorporates the uncertainty and fuzziness of decisions but also reflects the behavior of people who hesitate to provide positive feedback during an emergency.
However, these studies are focused on ranking the evacuation alternatives without considering network flow simulation to evacuate as many aggrieved as possible.
To evaluate each pair of alternatives, a decision-maker should perform all n(n − 1)/2 judgments of alternatives. However, due to a lack of knowledge regarding specific alternatives, time limits, and the decision maker’s confined expertise regarding the problem, not all the evaluations can be given by a specific decision-maker, which causes missing assessments in a decision matrix. These missing elements lead to incomplete intuitionistic fuzzy preference relations [18, 39] and, when there is a group of experts, to incomplete intuitionistic fuzzy group preference relations. When a decision-maker is not forced to provide all the existing preferences in a decision matrix, the process of decision-making becomes smooth and more effective.
1.5. Contraflow
Contraflow techniques, or lane reversal, is a powerful tool to temporarily maximize the total capacity of the congested road section by reversing the movement along it. This evacuation response technique was presented by Kim and Shekhar [51] to increase the total flow that could reach the desired destination. The main benefit of this method was tofacilitate traffic toward the safe destination by using unoccupied arcs toward risk zones, as reported in a previus study byArulselvan [52] and Rebennack et al. [53]. During evacuation, traffic congestion is ubiquitous due to this uneven traffic distribution. Moreover, conventional evacuation models do not allow traffic to be transported toward risk areas, thus causing empty roads to be used for sources. Contraflow techniques [54-56] suggest using empty arc capacities to increase the total number of aggrieved from the source.
1.6. Motivation
Combining evacuation models based on flow movement with incomplete intuitionistic preference relations tools of decision-making, we propose a hybrid method of fuzzy emergency decision-making, which allows the maximum fuzzy number of survivors to be transported to the safe locations via storage at intermediate nodes based on ranking the evacuation nodes based on incomplete intuitionistic preference relation.
The present study aims to transport as many evacuees as possible in case of emergency from a dangerous area to a safe location in a fuzzy dynamic network. The considered network allows intermediate storage at nodes, thus providing the safest pattern of evacuation by transporting more evacuees than those without intermediate storage. Furthermore, the network of a study allows lane reversal to maximize the total number of survivors by changing the traffic direction. An incomplete intuitionistic fuzzy preference relation is incorporated into the process of decision-making in order to find the best priority order of intermediate nodes for the transportation of the aggrieved.
2. METHODOLOGY
2.1. Preliminaries and a Fuzzy Dynamic Evacuation Model with Intermediate Storage Using Lane Reversal
Consider basic definitions underlying the proposed algorithms.
2.1.1. Definition 1
Fuzzy evacuation dynamic network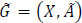 
is a network that includes two sets: a set of nodes X = {x1, x2, ... xn} and the set of arcs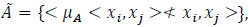 
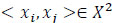with the defined membership function µA (xi, xj).
Consider a fuzzy dynamic network in the form of a directed graph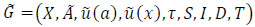 
, where X is the set of nodes, 
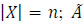is the set of fuzzy arcs, 
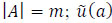designates the fuzzy capacity of the arc 
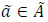. The arc capacity 
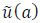for all 
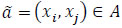indicates the maximum amount of flow that may enter the arc a from its tail xi per time. Therefore, if a flow starts from xi at time θ to move xj, it reaches xj at time 
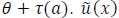designates the storage capacity of the node x, which limits the amount of flow allowed to store at xτ(a) is the transit time of the arc 
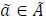which needs for flow to traverse from the tail to the head of the node; S is the set of sources; I is the set of intermediate nodes; D is the set of sinks, T is the given parameter, which reflects the feasible time during which the evacuation must be completed. T is divided into time steps T = {0, 1, ..., T}. For 
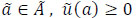and 
, 
.
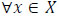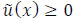For an arc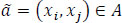 
, the node xi ε A is known as a tail node tail(a) = xi. xj ε X is considered as a head node head(a) = xj. The set of arcs going from the node xi is 
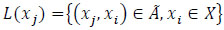and the set of incoming arcs to the node xi is 
.
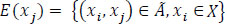2.1.2. Definition 2
Let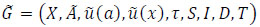 
be a given dynamic network. The time-expanded copy of the initial dynamic network is the static network 
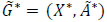in which X* = {xi(θ), xi(θ+1), xi ϵ X, θ = 0, 1, ... T} . If the flow can be stored at nodes, we suppose holdover arcs to exist 
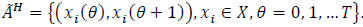. Thus, the set of arcs 
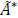of the static time-expanded network is 
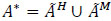, where AM be the set of movement arcs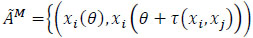 
.
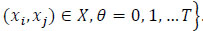Let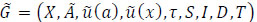 
be a dynamic evacuation network with intermediate storage, 
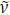be the dynamic S-D flow such as 
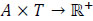and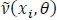 
, 
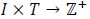be the amount of flow that is stored at intermediate nodes within time θ ϵ T. Therefore, the dynamic flow model with intermediate storage is given in Eqs. (1-4).
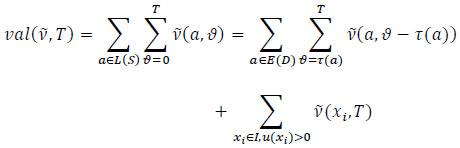
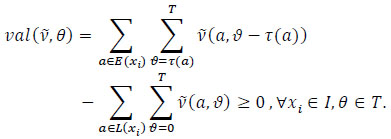
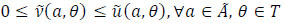
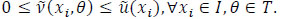
where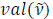 
maximizes the Objective (1) regarding the constraints (2-4). Eq. (2) illustrates that the total amount of flow from the sources does not necessarily reach the sinks but can be located at intermediate nodes without violating node capacity constraints. Eqs. (3-4) reflect the upper limits of the flow along the arc and at the intermediate node.
2.2. Incomplete Intuitionistic Fuzzy Preference Relations
Intuitionistic fuzzy preference relation [39] is represented by a matrix P = (pij)nxn on a set of n alternatives A = {a1, a2,...,an} , each element of which pij = (µij, vij, πij) is an intuitionistic fuzzy value (IFV), called an intuitionistic fuzzy number (IFN). In IFN, µij is the certainty degree (satisfaction degree), which shows the degree to which the alternative ai is preferred to the alternative aj; vij is the certainty degree (dissatisfaction degree), which shows the degree to which the alternative ai is non-preferred to the alternative aj under following conditions: µij, vij ϵ [0,1], 0 ≤ µij + vij ≤ 1, µji = vji, µii = vii = 0.5 for all i, j = 1, ... n. Indeterminacy degree πij = 1-(µij + vij) shows the level of the decision-maker’s hesitation regarding the preferences.
Consider operations with preference values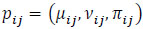 
and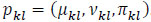 
:
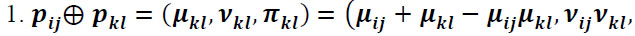
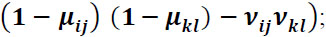
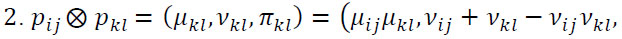
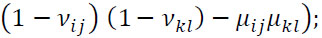
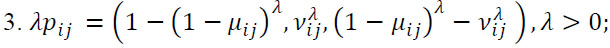
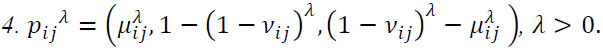
P is called a consistent intuitionistic preference relation if it satisfies the multiplicative transitivity:
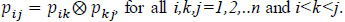
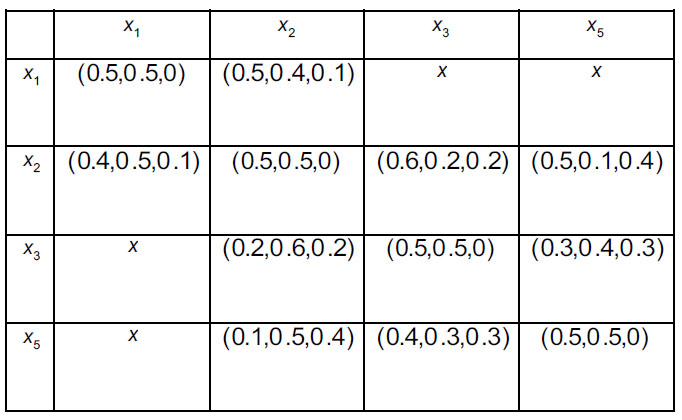
Consider incomplete intuitionistic fuzzy preference relation to compare each pair of evacuation alternatives. This type of relation allows missing elements in a decision matrix to exist due to insufficient decision-maker’s knowledge regarding specific pairs of alternatives.
2.2.1. Definition 3
Let P = (pij)nxn be an intuitionistic fuzzy preference relation, where pij = (µij, vij) for all i, j = 1, ... n. P is called an incomplete intuitionistic fuzzy preference relation if some elements are unknown, i.e., cannot be provided by a decision-maker. These missing elements will be denoted by the variable “x” while others exist and satisfy the conditions:
µij, vij ϵ [0,1], 0 ≤ µij+vij ≤ 1, µji = vij, µij = vji, µii = vii = 0.5 for all pij ϵ ∆, where ∆ is the set of existing elements in P.
If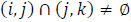 
, then the elements pij and pkl in P = (pij)nxn are called adjoining. If the element pij is missing, it can be calculated by two existing adjoining elements pik and pkj. In this case, preference relation P is called acceptable. An acceptable incomplete intuitionistic preference relation requires at least one known element in each row or column of R.
2.3. Hybrid Emergency Decision-making Algorithm
Let us consider a hybrid emergency decision-making algorithm (HEDM) combining incomplete intuitionistic fuzzy preference relations (IIFPR) and maximum dynamic flow (MDF) finding with intermediate storage based on lane reversal in order to transfer the maximum number of people from far away from the hazard.
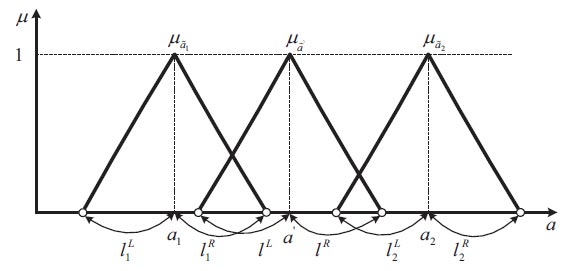
Defining the membership function µa'(a).
2.4. Finding the Borders of a Fuzzy Number
The proposed algorithm tackles fuzzy information in the form of fuzzy values in a fuzzy transportation network rather than other types of networks [58-61]. Arithmetic operations with fuzzy numbers are time-consuming. Moreover, they lead to the strong expansion of the final fuzzy number [14] and obtain unreliable solutions. To address this issue, a method based on linear combinations of spreads was proposed. To calculate the deviations of the desired number, the required value can be defined by adjacent values. Let the fuzzy parameter “near a'” be between two adjacent values “near a1” and “near a2” (a1 ≤ a' ≤ a2), whose membership functions µa1(a1) and µa2(a2) have a triangular form. Therefore, the spread of the membership function µa'(a) that corresponds to the fuzzy parameter “near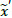 
" are set by a linear combination of the left and right spreads of adjacent values (Eq 7):
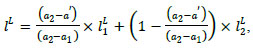
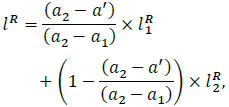
where lL is the left spread of the fuzzy triangular number with the center a1 – the right spread of the fuzzy triangular number with the center a2.
Fig. (1) illustrates a connection between a membership function of a fuzzy number membership functions of adjacent triangular numbers. When the center of a desirable triangular number is equal to the value existing on the number axis, the spreads of the fuzzy parameter coincide with the spreads of the existing number. If the center of a fuzzy parameter is located to the left of the center of the first value on the number axis, its spreads coincide with those that are located on the axis. In addition, when the center of the desirable number is to the right from the center of the last number marked on the axis, the spreads coincide as well.
Consequently, the centers of triangular numbers will be handled, while the spreads will be found at the final steps of the algorithm.
3. RESULTS AND DISCUSSION
Let us simulate the case of emergency decision-making when evacuation of the maximum possible number of survivors is needed from the hazard areas to the safe locations d1 and d2. The evacuation is performed according to the safe pattern as the storage at nodes is allowed, which enables saving the maximum amount of aggrieved. The priority order of shelters and intermediate nodes can be found by decision-making based on incomplete intuitionistic preference relation.
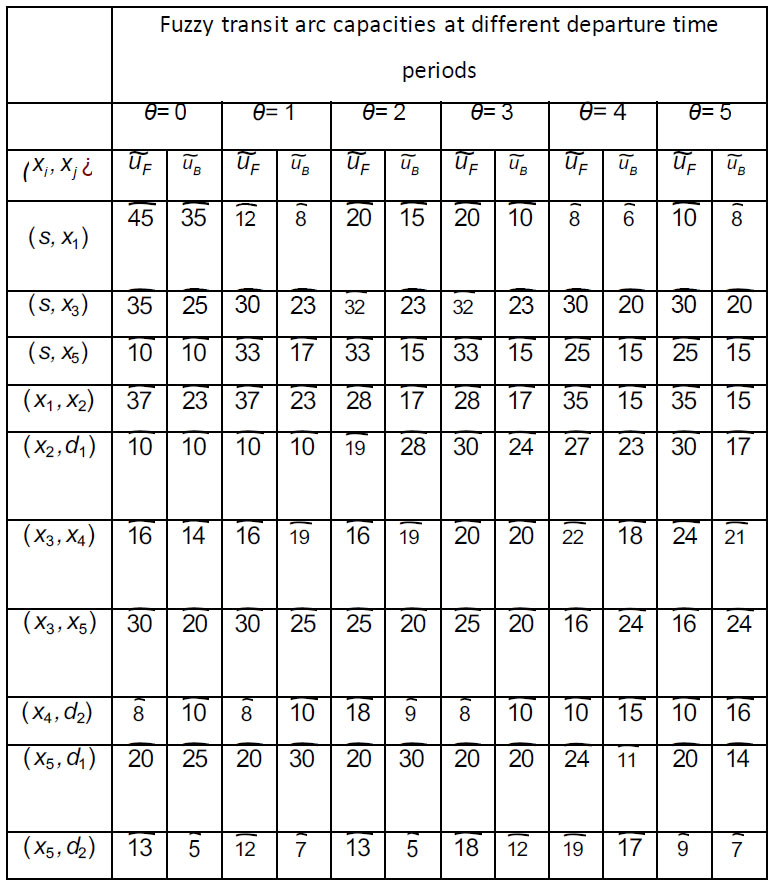
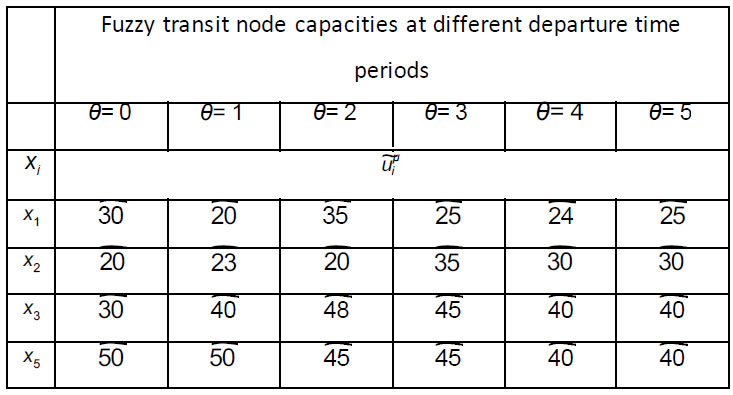
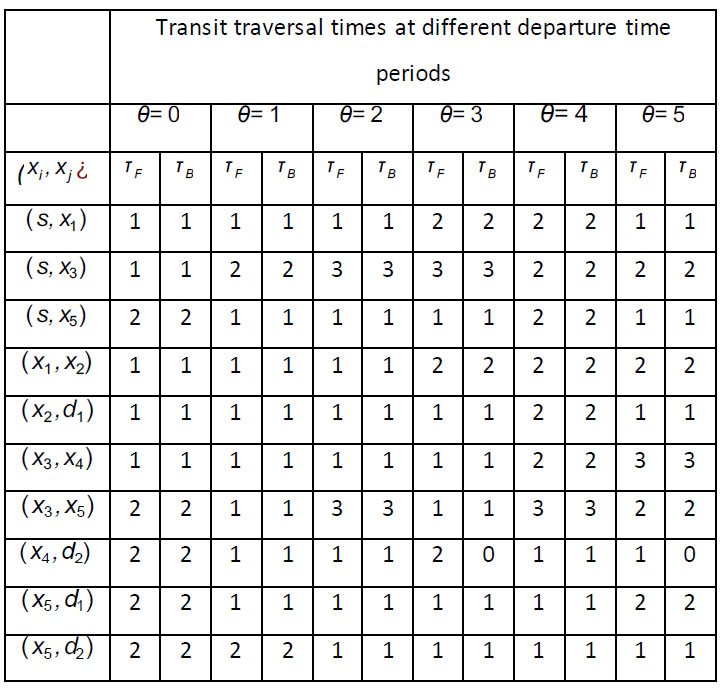
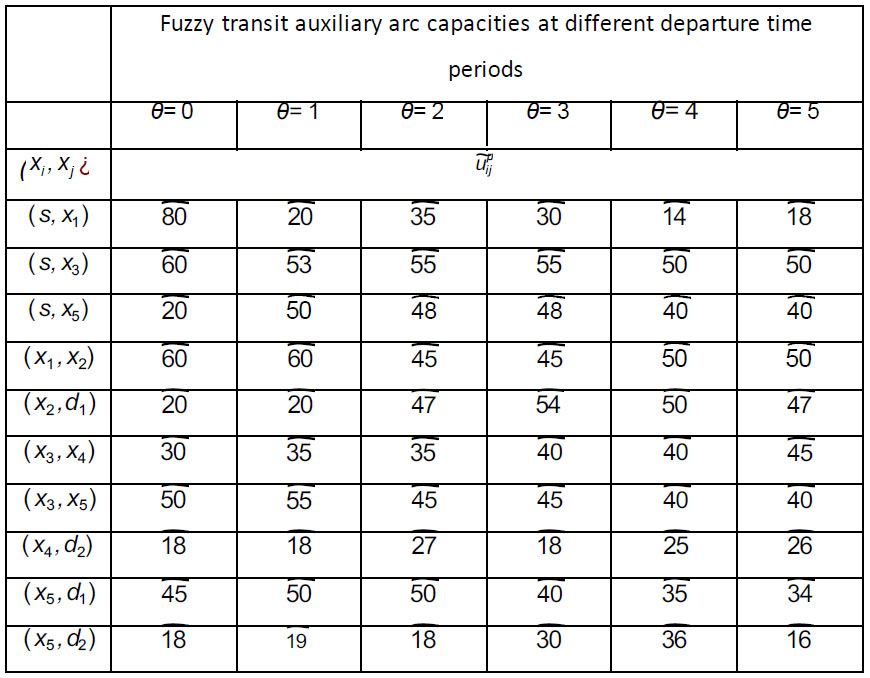
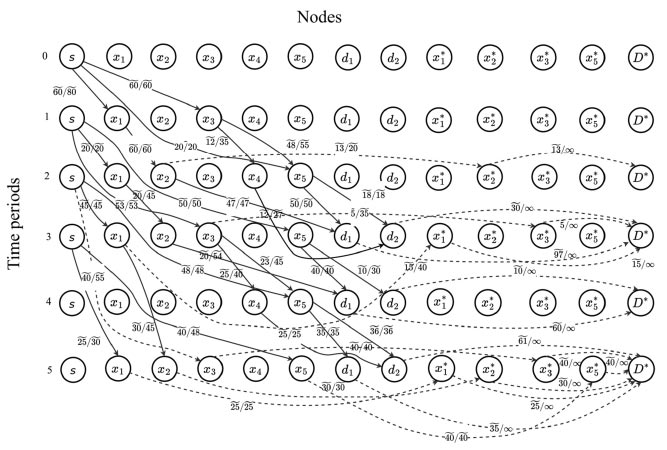
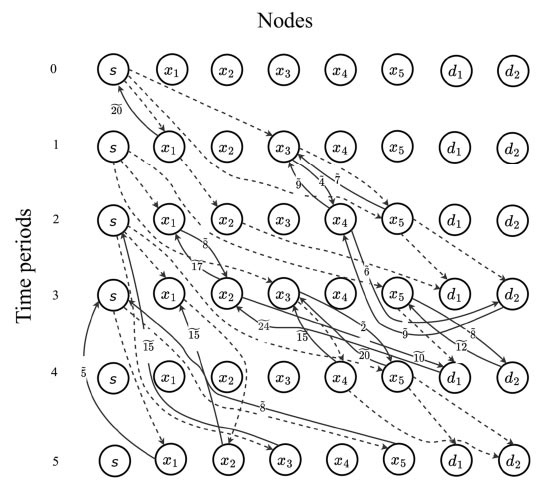
Fig. (2a) shows the initial dynamic fuzzy evacuation network with intermediate storage in the form of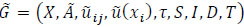 
with the dangerous area s as well as sinks d1 and d2 within the time horizon T=5. Transit fuzzy arc capacities, transit node capacities, and time-varying time parameters for the given network in Fig. (2a) are shown in Tables 1-3. Fig. (2b) illustrates the auxiliary dynamic network with lane-reversal, whose arc capacities are shown in Table 4. Dummy sinks x1*, x2*, x3*, x4*, x5* will be created for the corresponding intermediate nodes and connectedwith the nodes (Fig. 2c). Arc capacities of dummy arcs are equal to node capacities of intermediate nodes, which are shown in Table 3. Then, a super-sink will be added and connected with dummy sinks as well as initial sinks using the infinite arc capacities (Fig. 2c).
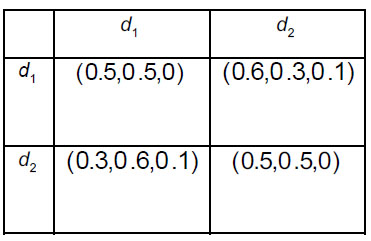
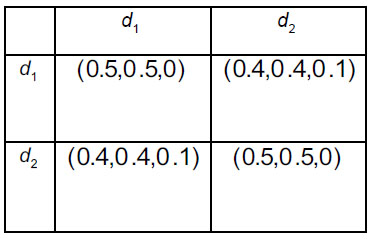
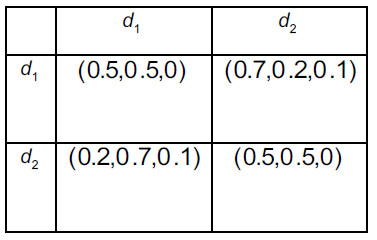
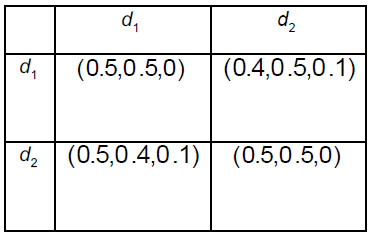
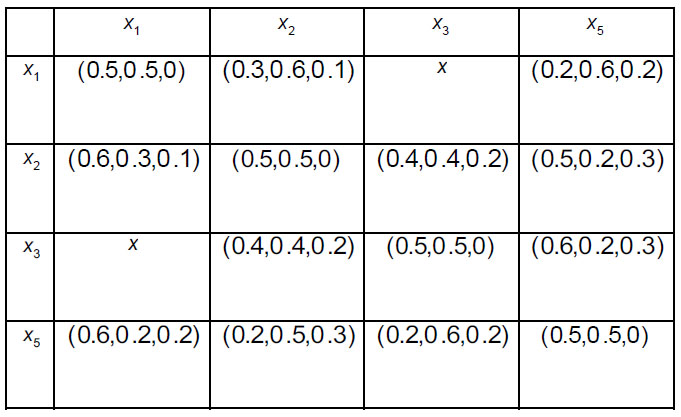
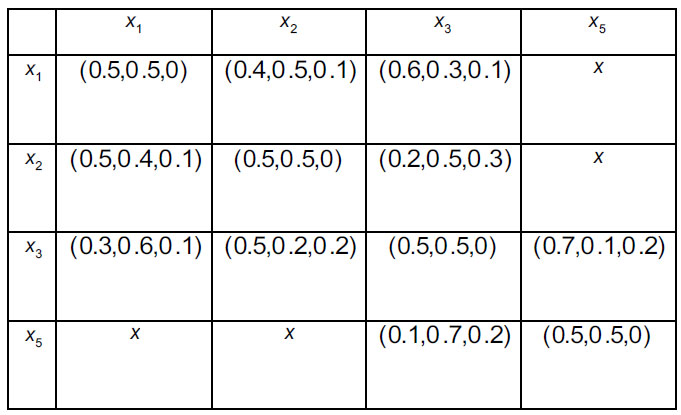
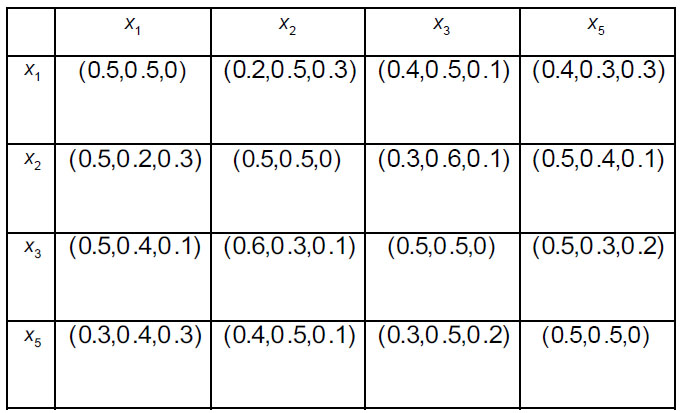
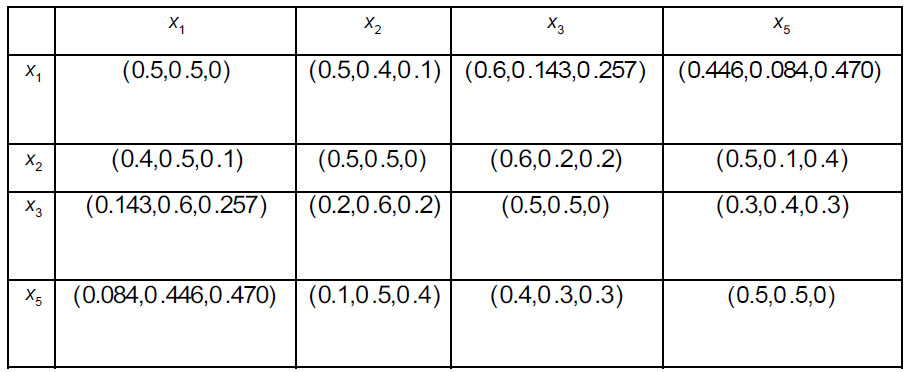
In order to prioritize sinks and intermediate nodes for evacuation (2 sinks An' (n 1,2) , and 4 intermediate nodes An* (n = 1, ... 4) follow the steps 3.1-3.5 of the Algorithm. Four decision-makers Dk(k = 1,2,3,4) whose weight vector is ω = (0.2, 0.24, 0.41, 0.15)T were asked to provide their preferences regarding alternatives. They assessed each pair of shelters using intuitionistic fuzzy preferences. A specific decision-maker may not have enough knowledge regarding the superiority of one alternative over another in a specific pair of alternatives, and that is why they may assess intermediate nodes in the form of incomplete intuitionistic fuzzy preferences. Consequently, decision-makers construct intuitionistic fuzzy preference relations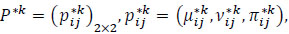 
i, j = 1,2; k = 1,2,3,4) (Tables 5-8) and incomplete intuitionistic fuzzy preference relations 
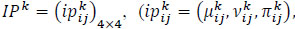i, j = 1,...,4; k = 1,2,3,4) (Tables 9-12):
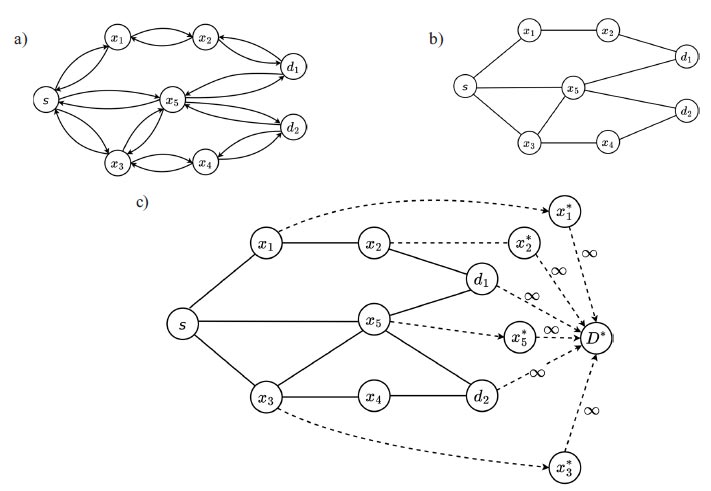
(a) Initial dynamic evacuation network with intermediate storage; (b) Auxiliary dynamic evacuation network with contraflow; (c) Modified dynamic evacuation network with dummy sinks and a super-sink.
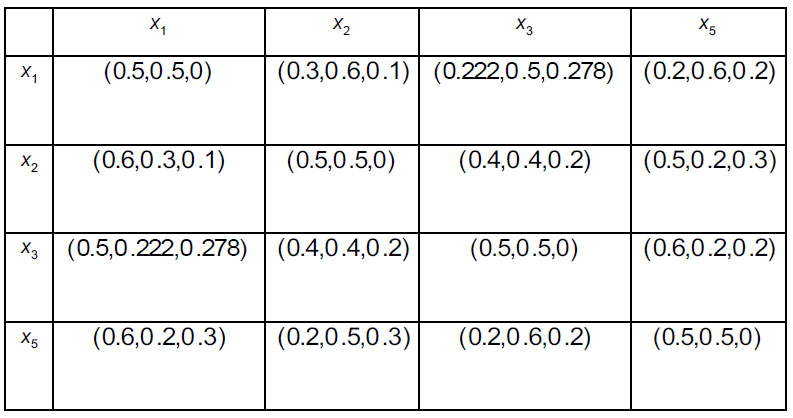
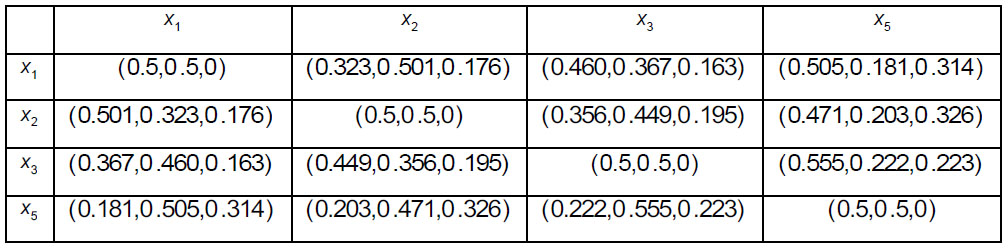
Calculacxisting adjoining elements by the Eqs. (5-6) in order to construct complete intuitionistic preference relations (Tables 13-15).
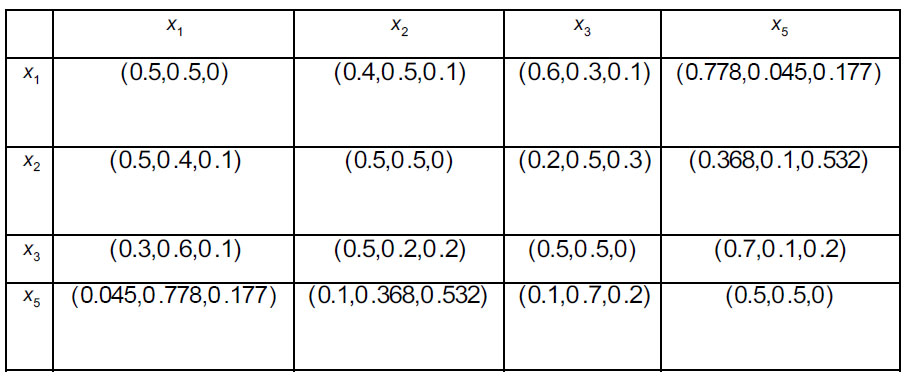
Construct the collective complete intuitionistic preference relation P^* based on fuzzy weighted averaging operator (Tables 16-17).
Find the total intuitionistic preference value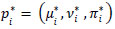 
and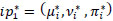 
of the alternative Ai.
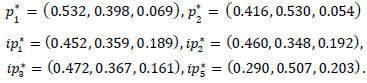
Compare all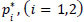 
by eq. and 
.
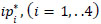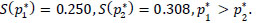
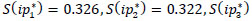
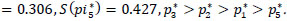
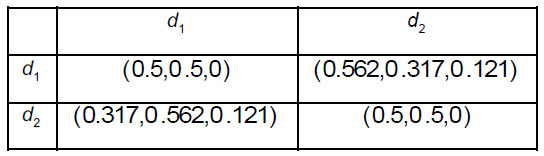
Therefore,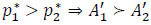 
, which means that the sink d1 has the higher priority than the sink d2.
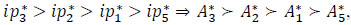, which means that the shelter x3 is if the highest rank.
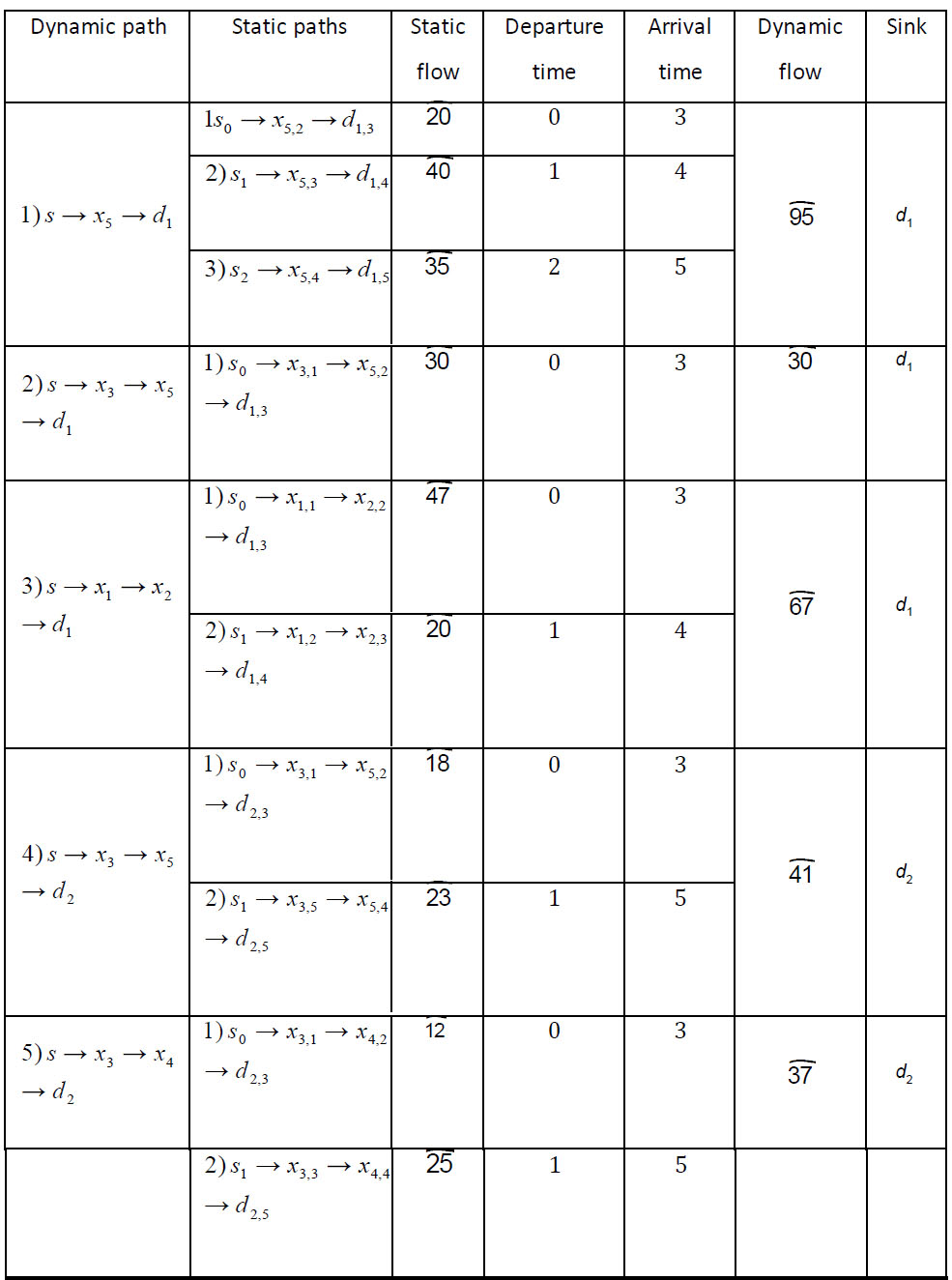
Construct a time-expanded static copy of the given network with lane reversal (Fig. 3) by creating a node-arc copy of each node at each time period with a time horizon and find the maximum number of aggrieved to the sinks with the order d1 > d and then to dummy sinks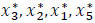 
.
Here the static time-expanded paths s 0 → x5,2 → d1,3, s1 → x5,3 → d1,4, s2 → x5,4 → d1,5, s 0 → x3,1 → x5,2 → d1,3, s 0 → x1,1 → x2,2 → d1,3, s1 → x1,2 → x2,3 → d1,4 are traversed to push 
and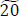 
flow units respectively to the sink d1. Then the paths s 0 → x3,1 → x5,2 → d2,3, s1 → x3,5 → x5,4 → d2.5, s 0 → x3,1 → x4,2 → d2,3, s1 → x3,3 → x4,4 → d2,5, s1 → x5,3 → d2,4, s2 → x5,4 → d2,5 are used to push 
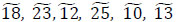flow units respectively to the sink d2. Fig. (4) shows a static time-expanded network containing the value of the maximum flow without intermediate storage.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
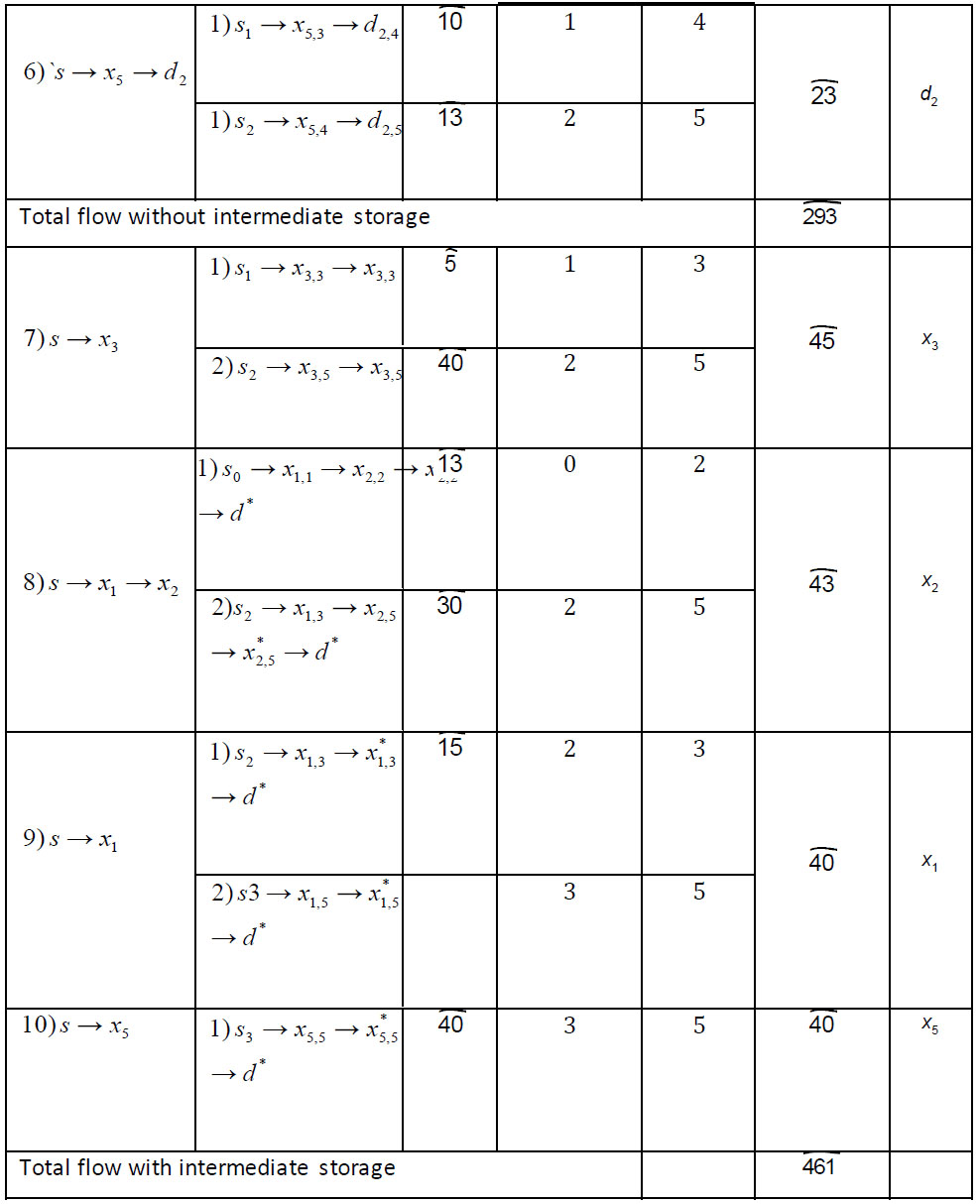
Furthermore, the paths s1 → x3,3 → x3,3* → d* and s2 → x3,5 → x3,5* → d* are used to push 
and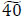 
units of flow to the dummy sink 
.
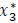The paths s 0 → x1,1 → x2,2 → x2,2* → d* and s2 → x1,3 → x2,5 → x2,5* → d* are used to push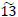 
and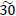 
flow units to the dummy sink 
.
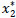The paths s2 → x1,3 → x1,3* → d* and s3 → x1,5 → x1,5* → d* transmit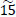 
and 
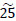flow units respectively to the dummy sink 
.
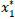Finally, the path s3 → x5,5 → x5,5* → d* pushes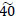 
flow units to the dummy sink 
.
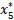Fig. (5) illustrates a static time-expanded network with the maximum flow with intermediate storage.
Table 18 shows flow distribution and total flow value in a network.
A static time-expanded network with contraflow.
A static time-expanded network with maximum flow without intermediate storage.
 |
 |
A static time-expanded network with maximum flow with intermediate storage.
Maximum dynamic flow with saved arc capacities.
The dummy sinks will be removed so that the initial network with the total maximum flow is the network with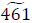 
units, where
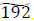and 
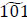flow units reached d1 and d2, respectively.
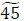flow units are stored at x3, 
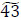flow units are stored at x2, 
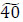flow units are stored at x1 and 
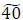flow units are stored at x5. According to Step 14 of the Algorithm, the following arcs are reversed completely: x3,1 → s 0, x5,2 → s 0, x5,3 → s1, x2,2 → x1,1, x1,2 → s1, x3,3 → s1, x1,3 → s2, x5,4 → s2, d2,4 → x4,4, d1,5 → x5,4, d2,5 → x5,4, d1,4 → x5,3, d1,3 → x2,2, d1,3 → x5,2, d2,3 → x5,2.
The following arcs x3,1 → x 0, x5,2 → x3,1, x1,5 → s3, x2,5 → x1,3, x3,5 → s2, x5,5 → s3, x4,4 → x3,3 are partially reversed up to capacities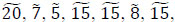 
respectively.
Each of the arcs x3,1 → s 0, x5,4 → x3,3 has a saved arc capacity of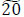 
units; each of x2,5 → x1,3, x3,5 → s2, x4,4 → x3,3 that of 
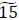; each of x5,5 → s3, x5,3 → d2,4, x1,2 → x2,3 that of 
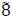units; each of x4,2 → x3,1, d2,3 → x4,2that of 
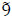units; arc x5,2 → x3,1-
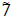units; x1,5 → s3-
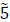units; d2,4 → x5,3-
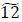units; x3,1 → x4,2-
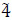units; x2,3 → x1,2-
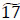units; x4,2 → d2,3-
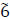units; x3,3 → x5,4-
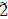units; x2,3 → d1,5-
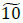units; d1,5 → x2,3-
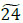units. Fig. (6) illustrates the maximum dynamic flow with saved arc capacities.
To calculate the spreads of the total fuzzy number with the center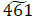 
units, apply Eq. (7) to the assessments of a decision-maker shown in Fig. (7), which illustrates the spreads of basic numbers.
Find the deviations based on Eq. (7). The desired flow value is among two adjacent basic values of the arc capacities: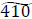 
with the left spread 
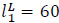, the right spread 
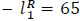and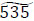 
with the left spread 
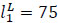, the right spread– 
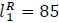. Based on Eq. (7): 
, 
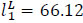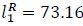. Round down the left and right spreads according to the concept of a fuzzy number. Finally, the maximum evacuation flow in the dynamic fuzzy network with the partial lane reversal can be represented by fuzzy triangular number (394, 461, 534) units.
To show the validity of the presented algorithm [18], let us compare its results with the method presented by Xu in [39], which is shown in Table 19.
Therefore, Xu, 2007 operator gives the following ranking order of evacuation alternatives: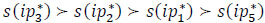 
. It means that 
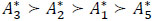compared with 
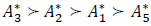for Xu, 2011 (Fig. 8).
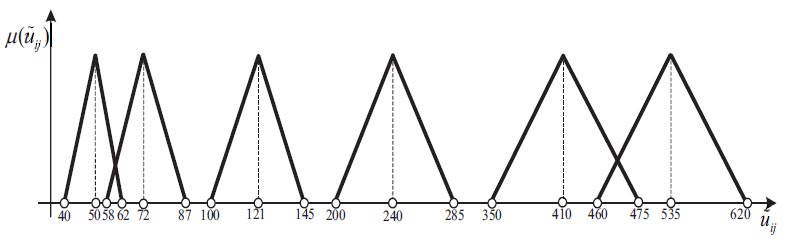
Membership functions of the basic values of arc capacities of the evacuation network in Fig. (2).
 |
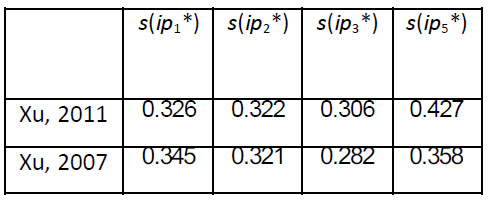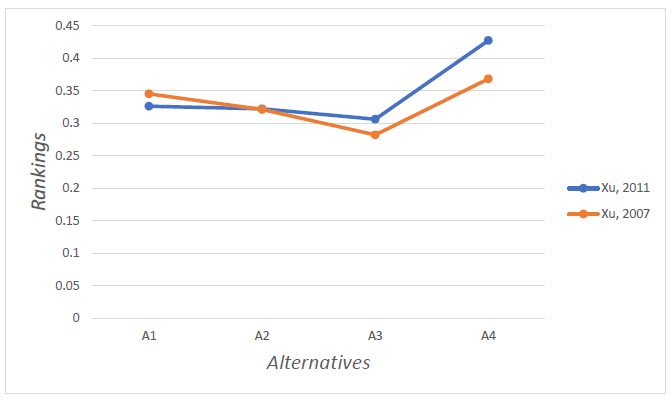
The results of Xu, 2011 and Xu, 2007 methods.
The results of estimations give the same order of alternatives. The difference between these two algorithms lies mostly in the formula for finding the missing elements. Xu, 2007 algorithm leads to a decrease in the membership degrees and an increase in the non-membership degrees of intuitionistic preference values, which may produce the distortion of the estimated information, but the estimation equations (5-6) in the Algorithm, which is motivated by the multiplicative transitivity of traditional fuzzy preference relations, can overcome this issue by making the estimated results more intuitive and reasonable. For evacuation modeling, it means that the order of nodes for evacuation leaves the same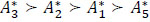 
. Therefore, the value of flow at the intermediate node remains the same.
The proposed hybrid algorithm allows transporting the maximum number of aggrieved from the dangerous area to safe destinations using the contraflow technique according to the safest scheme. i.e. by storing the evacuation flow at intermediate nodes based on the contraflow technique. This pattern transships as much flow as possible from the endangered area and stores the excess flow at temporary accommodation places. The lane reversal increases the outbound capacities, thus causing the increase in the total flow value. The saved values of arc capacities enable rescue services to facilitate the evacuation by location emergency services along the saved parts of roads. The priority order of safe locations and intermediate accommodation places is determined by the incomplete intuitionistic preference relation, which considers a lack of experts’ knowledge regarding specific alternatives, time pressure, or limited expertise related to the problem domain. Intuitionistic fuzzy values simulate hesitation and unsureness in experts’ reasoning, making decisions closer to the real emergency cases, which leads to more effective emergency decisions.
CONCLUSION
Disasters as uncertain disruptions can bring massive loss of human, infrastructure, and economic losses if not properly managed. To prevent the disaster or mitigate its devastating effects, making reasonable decisions for emergencies in a short time is needed. However, this process faces difficulties because of vagueness, uncertainty, and incompleteness of decision information. To handle the fuzziness of data, an incomplete intuitionistic preference relation is put forward in this paper to rank the evacuation alternatives. This relation allows missing elements in decision-makers’ matrices to be handled, which causes more effective decision-making in case of a lack of knowledge regarding some preferences.
A hazard area in the paper represents a dynamic network whose capacitated nodes are shelters, rooms, or road interseсtions; capacitated arcs show the connections between roads, for example, road sections or railways. Arcs of the evacuation network may have fuzzy transit arc capacities that depend on the departure time and transit traversal times, which are also time-varying. The method for transporting the maximum number of aggrieved from the hazard zone to safe locations based on contraflow was proposed that relies on the abilities of intermediate nodes to store the extra amount of flow, which was forwarded from endangered nodes. The contraflow technique allows for increasing the number of survivors by reversing the roads towards hazard locations in order to engage the rescue services. Furthermore, rescue services may be located at saved parts of the roads based on saved arc capacities found by performing the algorithm.
Overall, the paper integrates group emergency decision-making based on incomplete intuitionistic fuzzy preference relations and fuzzy macroscopic evacuation to find the effective order of intermediate nodes and shelters for evacuation, which is followed by finding the total number of the rescued.
A case study is conducted to simulate the process of evacuation and find the maximum possible evacuation flow value. As a part of our future research, we intend to incorporate interval-valued incomplete intuitionistic preference relations and iterative algorithms for improving the consistency of intuitionistic preference relations in emergency decision-making regarding evacuation alternatives. The practical application of the present study and future studies lies in the field of real emergency decision-making when an emergency happens, and experts have doubts while assessing evacuation alternatives regarding the attributes, especially when ambiguity of environment exists. The proposed approach leads to comprehensive and reliable solutions in complex emergencies when some features are unknown and lack statistics.
AUTHORS’ CONTRIBUTION
The author confirms sole responsibility for the: study conception and design, data collection, analysis and interpretation of results, and manuscript preparation.
LIST OF ABBREVIATIONS
| NPP | = Nuclear Power Plant |
| GIS | = Geographic Information Systems |
| AHP | = Analytical Hierarchy Process |
AVAILABILITY OF DATA AND MATERIALS
The authors confirm that the data supporting the findings of this study are available within the article.
FUNDING
The research was funded by the Russian Science Foundation Project No. 22-71-10121, https://rscf.ru/en/ project/22-71-10121/ implemented by the Southern Fed-eral University.
