RESEARCH ARTICLE
Effects of Rainfall on Driver Behaviour and Gap Acceptance at Multilane Roundabouts
Stephen Ibijola, Johnnie Ben-Edigbe*
Article Information
Identifiers and Pagination:
Year: 2018Volume: 12
First Page: 192
Last Page: 202
Publisher ID: TOTJ-12-192
DOI: 10.2174/1874447801812010192
Article History:
Received Date: 14/03/2018Revision Received Date: 22/4/2018
Acceptance Date: 8/5/2018
Electronic publication date: 14/6/2018
Collection year: 2018

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Background:
This paper filled an important gap in the behaviour of driver and gap acceptance model at multilane roundabouts by investigating their traffic performances during rainfall.
Introduction:
The study carried out an investigation into the impact of rainfall on driver’s behavioural changes and gap acceptance characteristics. Follow-up time headway and gap time were used as proxies.
Methodology:
Traffic volume, speed, vehicle type and headway data were collected at selected multilane roundabouts in Durban, South Africa. All surveyed roundabouts are within rain gauge catchment area of about 1km. Rainfall intensity was divided into three groups (light, moderate, and heavy). Dry weather data were used as control parameters.
Data Analysis:
Stepwise data analytical technique was used for ease of explanation and clarity. All model equations were tested for statistical fitness and deemed satisfactory for further analysis.
Conclusion:
Based on the synthesis of evidence obtained from driver’s behavioural changes and gap acceptance characteristics at multilane roundabouts, the paper concluded that it is correct to suggest that rainfall would have a profound effect on follow-up time headway and critical gap acceptance. However, the effect diminishes gradually as volume to capacity ratio approaches peak traffic operation. Once the threshold value of 0.85 is reached the diminishing effect of rainfall as the sole actuator of anomalous time headway increase is noticeable.
1. INTRODUCTION
There are the many factors that contribute to driver’s behavior at roundabouts. They include road infrastructure, vehicle type, traffic and ambient conditions according to Attivor et al. [1] Johnson [2], Ben-Edigbe [3]. The aim of this study is to investigate the driver behavioural changes and critical gap characteristics at multilane roundabout during rainy conditions. Follow-up time and critical gap parameters were used in the paper as proxies for driver behaviour and gap acceptance characteristics respectively. Critical gap is the minimum headway between successive vehicles in the circulating traffic flow. In general, critical gap is a parameter that depends on local conditions such as geometric layout, driver behaviour, vehicle characteristics, and traffic conditions. Follow-up time is the minimum time headway between two successive vehicles entering the roundabout if the available gap is big enough. In essence follow-up time is a time headway. The study is based on the hypothesis that rainfall irrespective of intensity has an effect on time headway and the critical gap at multilane roundabouts. The objectives are; to determine follow-up time ‘with and without’ rainfall, then compare the outcomes; also to determine circulating gaps between successive vehicles ‘with and without’ rainfall and compare the outcomes.
The roundabout is an at-grade priority intersection that operates on the yield rule where the entry vehicles give priority to the circulating vehicles. Yield rule operates on the availability of gap within the circulating traffic. Whenever a gap is available, the entry vehicle will look for the safe gap in the circulating traffic before accepting and entering the roundabout. Sometimes when safe gaps appear in circulating traffic stream, they are not taken by drivers entering the roundabout. Given that driver behaviour at roundabouts is precisely what the driver does, not what driver can or expected to do at roundabouts, drivers may elect to enter the roundabout when it is deemed unsafe. It raises the question of what exactly can be construed a safe gap. One thing is clear though, the available gap determines the number of the vehicles that can enter the roundabout. During rainy conditions at roundabouts, it is also useful to know the interaction of vehicle entering and circulating the central island. However, the key questions in this paper are; whether established and probable critical gap and follow-up time headway can be the same under dry and rainy conditions. Would there be significant differences along rainfall intensity line? It may be asked. The extent of driver behavioural changes and critical gap characteristics under rainy conditions has not been studied, hence the procedures adopted in this paper are novel.
2. MATERIALS AND METHODS
In previous studies, maximum likelihood Raff method [4], Ashworth method [5], Siegloch method [6], Wu method among others were used to estimate critical gap. Raff model is based on cumulative density function of the accepted and rejected headway. It relies on the intercept as the critical headway. Rodegerdts et al. [7] has shown that critical gap in the US is in the range of 3.7 to 5.5 s., Dahl and Lee [8] found that the critical gap to be between 3.5 to 6.1s in Canada. Manage et al. [9] showed that the critical gap in Japan ranged between 3.26 to 4.90 sec, while Qu et al. [10] reported that the critical gap was in the range of 2.6 to 3.2s in China. There is a consensus option among researchers that follow-up time and critical gap are key roundabout performance measures even though their values vary depending on the computation method used. So it is postulated that time headway has no fixed value. It varies relative to prevailing and computing conditions. In any case, Raff’s model is widely used in many countries owing to its simplicity and practicality even though Wu [11] mentioned that the critical headway based on the Raff does not consider the average of critical headway. The model is shown below in equation 1. It considers the prominence of major road traffic stream.
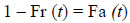 |
(1) |
Where; t is headway of major stream;
Fr (t) is the cumulative probability of rejected gap and Fa (t) is the cumulative probability of accepted gap.
Wu did not require any assumptions concerning the distribution function of critical gaps and the driver behavior, rather probability density function was used to estimate critical headways as shown below in equation 2.
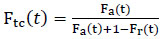 |
(2) |
Where: Ftc(t) = PDF of critical headway;
Fta(t) = PDF of an accepted gap t,
Fr(t) = PDF of a maximum rejected gap t.
If a time gap is sorted in an ascending order, critical headway is estimated with the equation 3
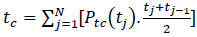 |
(3) |
Where Ptc(tj) is the frequencies of the calculated critical headways between j and j-1.
Ashworth’s [6] assumed that the headway of major stream follows a negative exponential distribution, whilst a critical gap and the accepted gap follow a normal distribution, Ashworth gave the calculation formula of a critical gap as follows:
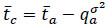 |
(4) |
Where; q is the flow rate of major stream (veh/s),  is the average critical gap (s),
is the average critical gap (s), 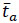 is average accepted gap (s), and
is average accepted gap (s), and 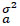 is the variance of accepted gaps (s2). The standard deviation of the accepted gaps (s) is shown below in equation 5 where ‘s’ is the standard deviation of the accepted gap (s), x is the accepted gap (s),
is the variance of accepted gaps (s2). The standard deviation of the accepted gaps (s) is shown below in equation 5 where ‘s’ is the standard deviation of the accepted gap (s), x is the accepted gap (s), 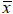 is the mean of the accepted gap (s) and ‘n’ is the total number of accepted gap.
is the mean of the accepted gap (s) and ‘n’ is the total number of accepted gap.
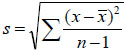 |
(5) |
Siegloch estimated critical gap using linear regression function where:
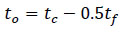 |
(6) |
However, Miller [12] modified equation 2 on the hypothesis that critical gap followed a distribution.
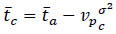 |
(7) |
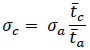 |
Where, 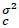 is the variance of critical gap (s2).
is the variance of critical gap (s2).
According to the US Highway Capacity Manual-HCM 2010, follow-up time (tf) and the critical gap (tc) can be estimated with equations:
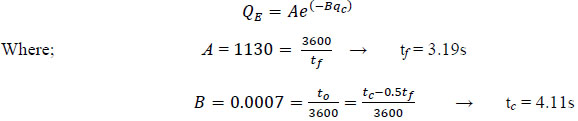 |
(8) |
Note that in equations 8, the parameters have fixed values for A and B. By implication, if the values of A and B can be computed by any valid method, follow-up time and critical gap can be estimated along HCM2010 [13] line, it can be argued.
However, in the United Kingdom-UK where vehicles observe the left hand rive rule just like in South Africa, linear regression is the most commonly used predictive model because it has inbuilt substantive geometric sensitivity and a correction factor for entry radius and entry angles. It has been shown in previous studies [12] that the linear relationship between entry and circulating flows can be modelled with equations 9 and adjusted with equation 10 according to Kimber [14].
 |
(9) |
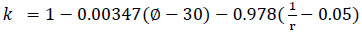 |
(10) |
Equation 10 takes into account different entry angles and entry radius, so that equation 9 is rewritten as;
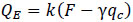 |
(11) |
However, if equation 11 is modified to include a dummy variable as shown in equation 12;
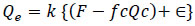 |
(12) |
Where; Qe = entry flow rate (pcu/h); Qc = circulating flow rate (pcu/h), F is the intercept and fc is the slope
Consider equation 12 again, when it rains, a dummy variable (ε) is introduced to depict that condition hence 1, otherwise zero for dry weather. The key parameter F allows influence of geometrical parameters like entry width, flare length and approach width to be determined. By adjusting F the slope of the linear equation that also contains the major capacity geometrical relationships is preserved. Average time headway for vehicles circulating the roundabout can be estimated and adjusted to a critical gap by taken into account average vehicle length given that the difference between headway and gap is the length of the lead vehicle. For example, assuming F is 1000 veh/h, the average follow-up time headway will be 3600/1000 = 3.6s. Assuming the average travel speed is 10m/s and the average vehicle length is 5m then the average gap time = 3.6 – [5/10] = 3.1s. In essence, a simple substitution of F for A and fc for B can be done when estimating follow-up time and critical gap. So, there is no need to build a new model. What is needed is a modification of relevant existing methods to accommodate for prevailing conditions. Shown below in Fig. (1) is an illustration of time headway (t) and degree of saturation (x) relationship. If is assumed that the degree of saturation is made up of five classes a, b, c, d and e, it can be postulated that once the optimum flowrate is reached at ‘e’ (Fig. 1), the impact of rainfall as the sole actuator of increase in time headway is no longer valid. Hypothetically, where the relationship between time headway and degree of saturation is shown as equation 13 then the differential between dry (D) and rainy (R) weather conditions can be estimated with equation 14.
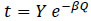 |
(13) |
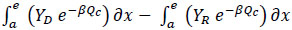 |
(14) |
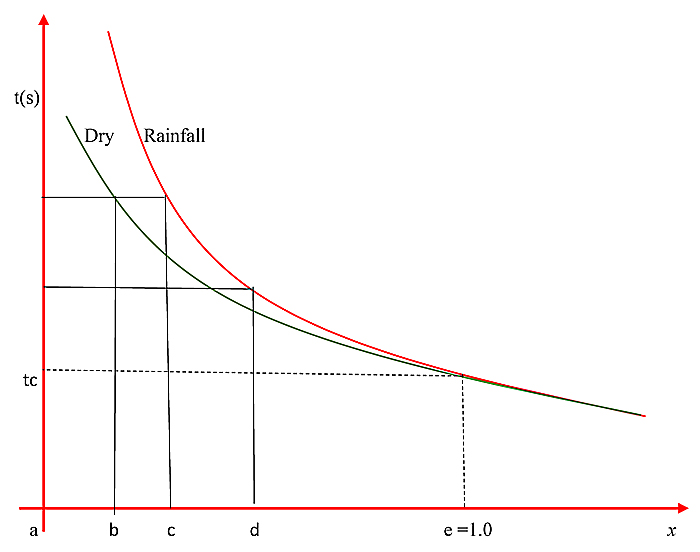 |
Fig. (1). Hypothetical time headway (ts) vs degree of saturation (x). |
2.1. Data Collection
Three classes of vehicles passenger cars, light vans, and bus/coach/truck were identified and three classes of rainfall intensity recorded; light (intensity < 2.5mm/h), moderate (2.5 ≤ intensity < 10 mm/h) and heavy (10 ≤ intensity < 50 mm/h) AMS [15]. The study used automatic traffic counter (ATC) to collect entry and circulating traffic flow data continuously for six weeks at each site. Four selected sites were surveyed in Durban, South Africa. Surveyed sites have bituminous surfaces, functional and effective drainage and located at about one km from the nearest rain gauge station. Note that time headway differs from gap because it is measured from the front bumper of the front vehicle to the front bumper of the next vehicle and also that follow-up time can be measured directly from observed data. The typical setup of a survey site is shown in Fig. (2) where ATC denotes automatic traffic counter, and RGS denotes rain gauge station. Geometric parameters for surveyed roundabouts are shown below in Table 1. Note that v denotes approach half width; e is entry width; r is entry radius, D is inscribed diameter; <o is entry angle; k is correction factor; E is entering vehicles; C is circulating vehicles; PC passenger is cars; LV is light vans; HB is heavy vehicles, trucks and buses.
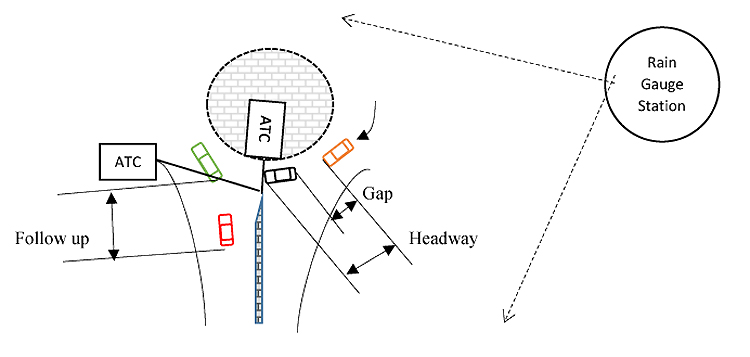 |
Fig. (2). Typical site set up. |
| Site | v (m) | e (m) |
r (m) |
D (m) |
<o | (k) | PC % | LV % | HB % | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | C | E | C | E | C | |||||||
| 01 | 7 | 10 | 30 | 50 | 50 | 95 | 94 | 92 | 4 | 7 | 2 | 1 |
| 02 | 8 | 10 | 45 | 55 | 45 | 98 | 91 | 97 | 8 | 1 | 1 | 2 |
| 03 | 7 | 12 | 30 | 50 | 55 | 93 | 89 | 94 | 9 | 5 | 2 | 1 |
| 04 | 7 | 10 | 35 | 55 | 45 | 97 | 95 | 93 | 4 | 6 | 1 | 1 |
3. RESULTS
Results are presented in a stepwise way for ease of clarity as follows:
Step 1: Determine the roundabout geometric profiles and rainfall precipitation classes as light, moderate and heavy. Record the entry and circulating traffic flows under dry, light, moderate and heavy rainy weather conditions as shown below in Tables 2 and 3, using appropriate passenger car equivalent values to convert from vehicles per hour to pcu per hour. Modify pcu values if at all necessary and note that such modifications will not change the study outcomes.
| – | Rainfall | |||
|---|---|---|---|---|
| Period | Dry | L | M | H |
| 1 | 828 | 521 | 712 | 629 |
| 2 | 607 | 780 | 712 | 703 |
| 3 | 852 | 821 | 492 | 657 |
| 4 | 1053 | 667 | 501 | 734 |
| 5 | 1070 | 676 | 897 | 593 |
| 6 | 787 | 732 | 619 | 729 |
| 7 | 796 | 664 | 679 | 813 |
| 8 | 864 | 734 | 463 | 1021 |
| 9 | 1048 | 842 | 741 | 744 |
| 10 | 1202 | 955 | 969 | 693 |
| 11 | 607 | 928 | 888 | 624 |
| 12 | 979 | 1079 | 979 | 864 |
| Rainfall | ||||
|---|---|---|---|---|
| Period | Dry | L | M | H |
| 1 | 1286 | 1093 | 1076 | 902 |
| 2 | 1385 | 1004 | 988 | 969 |
| 3 | 1382 | 1092 | 960 | 938 |
| 4 | 1123 | 1006 | 960 | 954 |
| 5 | 1181 | 1100 | 984 | 874 |
| 6 | 1490 | 1228 | 1200 | 1120 |
| 7 | 1464 | 1288 | 1101 | 1027 |
| 8 | 1336 | 1262 | 1097 | 919 |
| 9 | 1063 | 1001 | 1076 | 906 |
| 10 | 1075 | 1099 | 912 | 956 |
| 11 | 1665 | 1099 | 936 | 1004 |
| 12 | 1123 | 876 | 888 | 946 |
Step 2: Use the traffic data in step 1 in conjunction with equation 12 to determine entry and circulating model equation and test for statistically fitness. Note that when it rains, a dummy variable (ε) is introduced to depict that condition hence 1, otherwise zero for dry weather as shown below in equation 15;
Coefficient of determination (R2) is above 0.5, which indicate that the model equations are reliable; t-test result was greater than 2.2 at 95% level of confidence which shows that the parameters used are significant, and the F test result was greater than 4 which indicates that the model equations did not occur by chance. Therefore, the statistical results are satisfactory, and the model equation is accepted for further analysis.
 |
(15) |
Step 3: Determine the correction factor (k) for the multilane roundabout; for example, where the entry angle is 550 and entry radius is 30m;
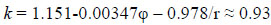 |
(16) |
Step 4: Apply the correction factor k-value in step 3 to the entry capacity model equation in step 2 and rewrite as
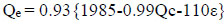 |
(17) |
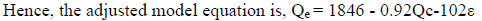 |
(18) |
Step 5: Estimate time headway, follow-up and critical gap for dry weather and rainfall where the degree of saturation at capacity, x = 1.0; at threshold, x = 0.85 and at free flow, x = 0.50. Where the average circulating speed (u) for dry weather is 11.11m/s (40km/h), for rainfall is 8.33m/s (30km/h) and average vehicle length (L) is 5m. Typical estimations of time headways are illustrated below and summarized in Table 4.
| Flow pce/h | x =1.0 | tf (s) | tc (s) | x=0.85 | tf (s) | tc (s) | x=0.50 | tf (s) | tc (s) |
| QE- dry | 923 | 3.90 | - | 785 | 4.59 | - | 462 | 7.79 | - |
| QE - rainfall | 872 | 4.13 | - | 741 | 4.86 | - | 436 | 8.26 | - |
| Qc - dry | 1003 | - | 3.14 | 853 | - | 3.77 | 502 | - | 6.72 |
| Qc - rainfall | 948 | - | 3.20 | 806 | - | 3.87 | 474 | - | 6.99 |
Entry capacity for dry, Qe = 1846/2 = 923veh/h/lane
Entry capacity for rainfall, Qe = [1846-102]/2 = 872veh/h/lane
Follow-up time (tf) or Entry time headway, (th) for dry = 3600 / 923 = 3.90s
Follow-up time (tf) or Entry time headway, (th) for rainfall = 3600 / 872 = 4.13s
Circulating capacity for dry, Qc = [1846/0.92]/2 = 1003veh/h/lane
Circulating capacity for rainfall, Qc = {[1846-102]/0.92}/2 = 948veh/h/lane
Circulating time headway, (tf) for dry = 3600 / 1003 = 3.59s
Circulating time headway, (tf) for rainfall = 3600 / 948 = 3.80s
Circulating gap time (tc) for dry = tf - (L/v or 5/11.11) = 3.59 – 0.45 = 3.07s
Circulating gap time gap (tc) for rainfall = tf - (L/v or 5/8.33) = 3.80 - 0.60 = 3.20s
Studies on the impact of rainfall on time headway at roundabouts have yet to be carried out, consequently it may not be possible to compare results with other studies. This study is merely pioneering a novel empirical approach and expecting to provoke debates on the effects of rainfall on time headways at roundabouts. Many researchers obtained different values of the critical gap for different roundabouts. If Siegloch model equation is employed in this example mentioned in step 5, the critical gap would have been 4.45s. HCM2010 [10] model equation would have yielded 4.11s, Ashworth (1968) model equation would have yielded 3.25s. Akcelik [16, 17] obtained a critical gap, tc = 4.89s. Akcelik [18, 19] also found that the fixed critical gap could not be applicable to all roundabouts. As shown below in Table 4, the empirical model yielded a critical gap of 3.14s when volume to capacity ratio = 1 under dry weather conditions; at the threshold value of 0.85, critical gap was 3.77s; under free flow conditions critical gap time was 6.72s (Fig. 3).
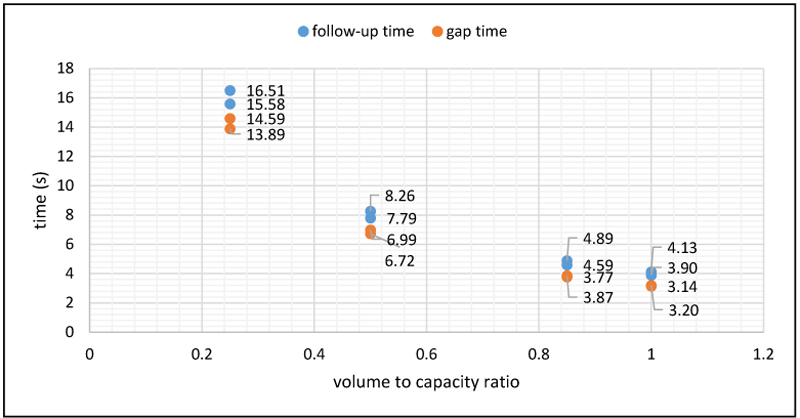 |
Fig. (3). Follow-up time and Gap vs Volume/capacity ratio. |
4. DISCUSSION
This study investigated the effect of rainfall on driver behavioural changes and gap acceptance characteristics at multilane roundabouts. Follow-up time headway and gap time were used as proxies for driver behavioural changes and gap acceptance characteristics. An empirical model technique that allowed only collated observed data was used. Simple linear regression was used to model entry and circulating traffic flow relationships under dry and rainfall weather conditions. It provided good and statistically satisfactory results. Whilst the method used in this study is useful, care should be taken when applied elsewhere, bearing in mind that the empirical methods have geometric design and circulating traffic flow limitations. As shown in Tables 5, 6 and 7, follow-up times and gap for dry weather are lower than follow-up times and gap for rainfall. When the lead vehicle accepts emerging gap, follow-up vehicle has to contend with the lead car behaviour and the rainfall conditions. At peak performance when the degree of saturation is at capacity, time differences between follow-up time and gap time are insignificant and in most cases anomalous. This is so because the effect of rainfall and peak period travel conditions cannot be separated. So, it is correct to say that once the optimum traffic flowrate is reached the influence of rainfall is nullified, thereafter the peak traffic conditions control time headway. Consequently, the effect of rain alone cannot be held solely responsible for time headway differentials without taking into account peak travel conditions.
| Site | Model Equations | Dry Flowrate pcu/h |
Rainfall Flowrate pcu/h |
Follow-up Time tf (s)±10% | Gap Time tc (s) ±10% | ||||
|---|---|---|---|---|---|---|---|---|---|
| Qe | Qc | Qe | Qc | Dry tf (s) |
Rainfall tf (s) |
Dry tc (s) |
Rainfall tc (s) |
||
| 01 k=0.95 |
QE = 2280-1.17Qc-146RL | 1083 | 926 | 1013 | 867 | 3,32 | 3,55 | 3.44 | 3.55 |
| QE = 2211-1.09Qc-302RM | 1050 | 964 | 906 | 817 | 3,43 | 3,97 | 3.28 | 3.81 | |
| QE = 2159-1.04Qc-345RH | 1026 | 986 | 861 | 829 | 3,51 | 4,18 | 3.20 | 3.74 | |
| 02 k=0.98 |
QE = 1967-1.23Qc-71RL | 964 | 784 | 929 | 756 | 3,73 | 3,88 | 4.14 | 4.16 |
| QE = 1908-1.17Qc-191RM | 935 | 799 | 841 | 719 | 3,85 | 4,28 | 4.06 | 4.41 | |
| QE = 1805-1.06Qc-264RH | 885 | 835 | 755 | 721 | 4,07 | 4,77 | 3.86 | 4.39 | |
| 03 k=0.93 |
QE = 1985-0.99Qc-110RL | 923 | 933 | 872 | 881 | 3,90 | 4,13 | 3.41 | 3.49 |
| QE = 2038-1.04Qc-270RM | 948 | 957 | 822 | 831 | 3,80 | 4,38 | 3.31 | 3.73 | |
| QE = 1900-0.92Qc-379RH | 884 | 961 | 707 | 761 | 4,07 | 5,09 | 3.30 | 4.13 | |
| 04 k=0.97 |
QE = 1902-1.19Qc-61RL | 922 | 832 | 892 | 773 | 3,90 | 4,04 | 3.88 | 4.06 |
| QE = 1716-0.88Qc-149RM | 832 | 980 | 760 | 894 | 4,33 | 4,74 | 3.22 | 3.43 | |
| QE = 1556-0.61Qc-183RH | 755 | 1279 | 665 | 1130 | 4,77 | 5,41 | 2.36 | 2.59 | |
| Site | Model Equations | Dry Flowrate (pcu/h) |
Rainfall Flowrate (pcu/h) |
Follow-up Time tf (s)±10% | Gap Time tc (s) ±10% | ||||
|---|---|---|---|---|---|---|---|---|---|
| Qe | Qc | Qe | Qc | Dry tf (s) |
Rainfall tf (s) |
Dry tc (s) |
Rainfall tc (s) |
||
| 01 k=0.95 |
QE = 2280-1.17Qc-146RL | 921 | 787 | 861 | 737 | 3.91 | 4.18 | 4.12 | 4.28 |
| QE = 2211-1.09Qc-302RM | 893 | 819 | 770 | 694 | 4.03 | 4.68 | 3.95 | 4.59 | |
| QE = 2159-1.04Qc-345RH | 872 | 838 | 732 | 705 | 4.13 | 4.92 | 3.85 | 4.51 | |
| 02 k=0.98 |
QE = 1967-1.23Qc-71RL | 819 | 666 | 790 | 643 | 4.40 | 4.56 | 4.96 | 5.00 |
| QE = 1908-1.17Qc-191RM | 795 | 679 | 715 | 611 | 4.53 | 5.03 | 4.85 | 5.29 | |
| QE = 1805-1.06Qc-264RH | 752 | 710 | 642 | 613 | 4.79 | 5.61 | 4.62 | 5.27 | |
| 03 k=0.93 |
QE = 1985-0.99Qc-110RL | 785 | 793 | 741 | 749 | 4.59 | 4.86 | 4.09 | 4.21 |
| QE = 2038-1.04Qc-270RM | 806 | 813 | 699 | 706 | 4.47 | 5.15 | 3.98 | 4.50 | |
| QE = 1900-0.92Qc-379RH | 751 | 817 | 601 | 647 | 4.79 | 5.99 | 3.96 | 4.96 | |
| 04 k=0.97 |
QE = 1902-1.19Qc-61RL | 784 | 707 | 758 | 657 | 4.59 | 4.75 | 4.64 | 4.88 |
| QE = 1716-0.88Qc-149RM | 707 | 833 | 646 | 760 | 5.09 | 5.57 | 3.87 | 4.14 | |
| QE = 1556-0.61Qc-183RH | 642 | 1087 | 565 | 961 | 5.61 | 6.37 | 2.86 | 3.15 | |
| Site | Model Equations X = 0.50 |
Dry Traffic Flowrate |
Rainfall Traffic Flowrate |
Follow-up Time tf (s)±10% | Gap Time tc (s) ±10% | ||||
|---|---|---|---|---|---|---|---|---|---|
| Qe pcu/h |
Qc pcu/h |
Qe pcu/h |
Qc pcu/h |
Dry tf (s) |
Rainfall tf (s) |
Dry tc (s) |
Rainfall tc (s) |
||
| 01 k=0.95 |
QE = 2280-1.17Qc-146RL | 542 | 463 | 507 | 434 | 6.65 | 7.11 | 7.33 | 7.70 |
| QE = 2211-1.09Qc-302RM | 525 | 482 | 453 | 409 | 6.86 | 7.95 | 7.02 | 8.21 | |
| QE = 2159-1.04Qc-345RH | 513 | 493 | 431 | 415 | 7.02 | 8.36 | 6.85 | 8.09 | |
| 02 k=0.98 |
QE = 1967-1.23Qc-71RL | 482 | 392 | 465 | 378 | 7.47 | 7.75 | 8.73 | 8.92 |
| QE = 1908-1.17Qc-191RM | 468 | 400 | 421 | 360 | 7.70 | 8.56 | 8.56 | 9.41 | |
| QE = 1805-1.06Qc-264RH | 443 | 418 | 378 | 361 | 8.14 | 9.54 | 8.17 | 9.39 | |
| 03 k=0.93 |
QE = 1985-0.99Qc-110RL | 462 | 467 | 436 | 441 | 7.80 | 8.26 | 7.27 | 7.57 |
| QE = 2038-1.04Qc-270RM | 474 | 479 | 411 | 416 | 7.59 | 8.76 | 7.07 | 8.06 | |
| QE = 1900-0.92Qc-379RH | 442 | 481 | 354 | 381 | 8.14 | 10.18 | 7.04 | 8.86 | |
| 04 k=0.97 |
QE = 1902-1.19Qc-61RL | 461 | 416 | 446 | 387 | 7.81 | 8.07 | 8.20 | 8.71 |
| QE = 1716-0.88Qc-149RM | 416 | 490 | 380 | 447 | 8.65 | 9.47 | 6.90 | 7.45 | |
| QE = 1556-0.61Qc-183RH | 378 | 640 | 333 | 565 | 9.54 | 10.83 | 5.18 | 5.77 | |
Although a slight improvement occurred when the degree of saturation is at the threshold value of 0.85, nevertheless the average follow-up time under dry weather conditions is 4.58s and 5.14s for rainfall, an increase of 12.2%. As for gap acceptance, the average time for dry weather conditions is 4.15s against 4.57s for rainfall, an increase of 10.1%. When the degree of saturation was set at 0.5, the average follow-up time under dry weather conditions is 7.78s and 8.74s for rainfall, an increase of 12.3%. As for gap acceptance time, the average for dry weather conditions was 7.36s against 8.18s for rainfall, an increase of 11.1%. In any case, the average follow-up time under dry weather conditions is 3.89s and 4.37s for rainfall, a 12.3% increase. As for gap acceptance time, the average for dry weather conditions is 3.46s against 3.79s for rainfall, an increase of 9.5%. So, it is correct to assert that irrespective of whether the drivers have priority at the roundabouts or not, they are restrained by rainfall.
The study also affirmed that Raff [15] HCM 2010 [10] and Ashworth [6] methods as significant, important and very useful theoretical techniques. Even though it was applied in this paper, the key advantage of Siegloch method [19] is the adaptability of a linear regression function. It can be used with linear regression to determine time headway and gap acceptance. The computed empirical follow-up time (3.89s) and critical gap (4.37s) under dry weather conditions are outside the prescribed Raff, Ashworth and HCM follow-up time where tf = 3.19s and critical gap, tc = 4.11s. The simple explanation is that computed times are based on observed data Raff and HCM 2010 times are based on gap acceptance theory, whilst Ashworth is overly dependent on statistical variance. In sum, rainfall triggered an increase in follow-up and critical time headway at all surveyed sites. Heavy rainy conditions have the most significant influence on time headway. However, further research into needed especially in the possibility of traffic shockwaves at roundabout caused by adverse weather conditions.
CONCLUSION
Based on the synthesis of evidence obtained from the impact of rainfall on time headway changes at multilane roundabouts, it is correct to conclude that rainfall would have a profound effect on follow-up time and critical gap. It is also correct to suggest that the time headways are anomalous because the time differentials are inconsistent with rainfall intensity. Time headway differences become smaller relative to rainy conditions and anomalous under heavy rainfall, thus suggesting that drivers are more cautious. However, once the degree of saturation threshold mark of 0.85 is reached and surpassed, the effect of rainfall as the sole traffic flow disturbance gradually diminishes. It is valid to conclude that the effect of rain alone cannot account peak travel conditions be held responsible for time headway differentials when traffic flow is operating at peak without taking into account peak travel conditions.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The author declares no conflict of interest, financial or otherwise.
ACKNOWLEDGMENTS
We are grateful to EThekwini Municipality, Durban and South Africa Police Service for their support and assistance with traffic control during and after installation of equipment. The study was supported by research funds from the University of KwaZulu-Natal, Durban, South Africa.








