All published articles of this journal are available on ScienceDirect.
Application of Bayesian Semi-Parametric and Hierarchical Models for Analyzing Dispersed Traffic Barriers Crash Data
Abstract
Introduction:
Despite the traffic barriers effectiveness in reduction of the severity of run-off road crashes, the severity of barrier crashes still accounts for a significant fraction of road fatalities. Although extensive research has already been conducted in studying traffic barrier crashes, those studies mostly either consider the severity or frequency of crashes. Here, the equivalent property damage only (EPDO) was used to account for both aspects of crashes. While modeling EPDO crashes, there are challenges associated with that type of dataset including its sparse distribution, and the presence of heterogeneity in the dataset due to aggregation of various crash types.
Methods:
Ignoring the sparse nature of the data might result in biased or even erroneous results. Thus, in this study we identify factors to barriers EPDO crashes while considering the discussed challenges. Those consideration are especially important as in the next step we will employ the modeling results for conducting the cost-benefit analysis. Two main methods were considered in this study to address the discussed challenges including parametric and non-parametric Bayesian hierarchical models. A semiparametric Bayesian approach was used to relax the normality assumption by using a mixture of multivariate Dirichlet prior, defining a flexible nonparametric model for the random effects’ distribution, and using grouping to account for the heterogeneity due to the structure of the dataset. On the other hand, Bayesian hierarchical models with two distributions of Poisson and negative binomial with similar levels of hierarchy were considered. These models were chosen as closest models to the Bayesian semiparametric model. The incorporated models were compared in terms of deviance information criterion (DIC).
Results and Discussion:
The results highlighted that although the semi-parametric method outperforms the Bayesian hierarchical model with Poisson distribution, the Bayesian hierarchical model with negative binomial (NB) distribution outperform the semi-parametric model. The findings might be related to the severe sparse nature of the EPDO, which cannot optimally be accounted by semiparametric approach, and the model needs more flexibility.
Conclusion:
It was found that being unrestrained, driving in interstate system, driving in clear weather, light conditions, and driving in a higher traffic all increase the likelihood of EPDO crashes. Also, while some predictors were significant in less accommodative models of semi-parametric or Poisson models, they were not for Negative binomial model.
1. INTRODUCTION
Road crashes claim many lives yearly, resulting in a tremendous economic loss. For instance, more than 1 million people die every year from traffic crashes, and 50 million more are severely injured [1]. Crashes are the leading causes of death in the U.S, falling behind only cancer and heart diseases [2]. The situation is of particular concern in a mountainous area like Wyoming, with one of the highest fatalities rates in the country [3]. One of the leading causes of this high crash fatality rate in the state is run-off-the-road (ROTR) crashes, resulting from factors such as mountainous and adverse weather conditions in winter.
Traffic barriers are a popular countermeasure for reducing roadside crashes' severity. Traffic barrier crashes are identified as the third most common cause of fixed object fatalities after trees and utility poles [4]. However, still, the severity of these crashes persists.
Given the importance of traffic barrier crashes, studies have been already conducted to identify factors of these crashes [5, 6]. Despite the efforts, few studies have been conducted considering both aspects of barrier crashes, including their severity and frequency.
There are still challenges associated with modelling equivalent property damage only (EPDO) crashes, including the sparse nature of crashes that traditional inferences could not model. The second challenge, which is common across most crash datasets, is accounting for the unobserved heterogeneity resulting from the dataset's structure, such as traffic barrier types.
In order to address the first challenge of data response sparsity and to have valid results, greater modelling flexibility and robustness against misclassification of a model specification are needed [7]. In the Bayesian context, the flexibility might be given through infinitely many parameters [8].
The second issue is not accounting for hierarchical structure, which might violate the assumption of independent residuals. That is since observation nested in the same group, or barrier types, share similar characteristics, and the model should account for them.
In this study, to evaluate the impact of various factors on the EPDO crashes, the analysis was conducted on the baseline distribution using the mixture Dirichlet process (MDP) prior, which is centered in a standard parametric family, or the Poisson distribution. The Bayesian hierarchical Poisson (BHP) model was used as a starting parametric model to account for the stochastic variation of crash count data. Also, Bayesian hierarchical models with two distributions, Poisson and Negative binomial, were compared with the Bayesian semiparametric method.
However, crash count typically shows more variation around theoretical distribution. The situation is more critical if the objective is to model the EPDO instead of crash count. Thus, the Bayesian hierarchical negative binomial (HNB) model was considered for modelling the sparse EPDO crashes. To provide a better perception of various barrier types, the included types are presented in Fig. (1).
The following paragraphs will review few studies that implemented semi-or non-parametric methods in the literature review. Then this study will present studies using hierarchical techniques.
1.1. Semi-or Non-Parametric Methods
Various semiparametric [9] and non-parametric methods have been proposed for modelling sparse datasets [10-12]. For instance, a study was conducted to estimate the relationship between crash counts and roadway characteristics [13]. A semiparametric Poisson-gamma model, with standard parametric assumption, was employed for the analysis; in that study, a quadratic regression spline was used for selecting the knot points. In another study, a semiparametric count data model was used to deal with the issue of individual heterogeneity, including temporal and spatial correlation and nonlinear covariate effects [14]. The study used regression splines with the negative binomial model for data related to automobile insurance claims.
Most past studies employed both Poisson and negative binomial models for modelling count data; those models assume an uncorrelated observation resulting in ignoring a correlation across groups. However, the hierarchical modelling of the above approaches could be used to account for correlation across groups in the dataset.
1.2. Bayesian Hierarchical Model
A previous study used Bayesian hierarchical models with various variables as hierarchies to analyze the corridor-level safety of an intersection [15]. The Hierarchical negative binomial (HNB) model was solely used in that study. Another study evaluated road network safety using Bayesian hierarchical modelling [16]. The result was compared with the standard negative binomial model, showing that the hierarchical modelling outperforms the other model.
A recently finite mixture model has been employed in the context of random effect and Bayesian hierarchical techniques to assign an objective hierarchy to the model, instead of a subjective choice [17]. For instance, the Bayesian hierarchical finite mixture model was used for modelling sparse crash data. In that technique, an objective hierarchy was used through a finite mixture model, resulting in a significant enhancement in model fit. In another study, a comprehensive discussion was made regarding the application of various methods for the evaluation of sparse datasets [18]. After conducting different goodness-of-fit measures, a hurdle model was proposed to accommodate observations with zero crashes and to account for a sparse distribution of EPDO crashes.

This study implements the hierarchical Bayesian models with two distributions, Poisson and negative binomial. Compared with the Poisson model, a negative binomial can handle overdispersion due to an introduced error term. However, the Poisson model was also used as a starting point for modelling stochastic variation of barrier EPDO counts.
It should be noted that not accounting for overdispersion by the suitable model might result in underestimating the variance of the estimated parameters. Although many studies implemented classical versions of Poisson and negative binomial models in highway safety [19-22], not that much research has been conducted using a hierarchical approach of those methods for modelling crash counts. Consequently, that could result in an inaccurate conclusion by underestimating the variability of the data.
1.3. Research Question
Important questions would be raised while implementing semiparametric methods:
- How good is the semiparametric model in predicting sparse response?
- How is the semiparametric model performance compared with similar advanced parametric modelling techniques that could account for the dataset's structure?
In this study, besides checking the performances of the model deviance information criterion (DIC), the models were compared in terms of changes in magnitudes, significance and estimated parameter variances. After highlighting the best fit model, the identified results are used as means of interpretation for policy making in the state.
2. METHODOLOGY
This section highlights the implemented methods of Bayesian semiparametric and parametric techniques.
2.1. Bayesian Semiparametric Method
The parametric model might not be able to account for the sparse nature of the response, and the unrealistic nature of the assigned distribution might result in biased and unsatisfactory results. For this scenario, non- or semiparametric methods could be used to gain robustness against misclassification of the parametric distributions. This could be achieved in the Bayesian context by placing a prior distribution on infinite dimensions or all probability distribution space. The Dirichlet process (DP) has been widely used in the probability distribution space to create a semiparametric model [23].
- · When random effects follow a multivariate normal distribution, the monotonic differentiable link function could be written as follows [7]:
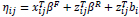 |
(1) |
Where ηij is a linear predictor,
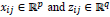 are p- and q-dimensional design vectors, βR and βF are means of random and fixed effects, and bi represents the subject-specific deviation from the mean.
are p- and q-dimensional design vectors, βR and βF are means of random and fixed effects, and bi represents the subject-specific deviation from the mean.
In order to avoid the effects of the misspecification of parametric random effects distribution and a better representation of the distributional uncertainty, a Bayesian semiparametric model could be used to incorporate a probability model for the random effects [7]. For this, the parametric assumption would be relaxed as follows:
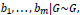 |
(2) |
where
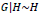 |
(3) |
Where H is probability distribution such as DP. It should be noted that if the mean of the estimates comes from some prior distribution G(.), and the prior distribution is uncertain and modelled as DP, then the data also come from Dirichlet mixture of normal [24].
However, the location of G is confounded by βR, and as more data are available, the posterior mass would no longer concentrate on a point in the model, which makes the analysis difficult [7]. So, to address this issue, the following re-parameterizations are considered, and equations 1, 2, and 3 could be transformed to the below equations [25]:
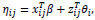 |
(4) |
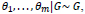 |
(5) |
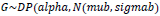 |
(6) |
Where βF is transformed to β, while βR+bi are transformed to θi, and non-parametric G is centered at Nq(µ, ∑) distribution. The precision or total mass parameter, alpha, of the DP prior could be considered random, having a gamma distribution (see equation 9). mub is the mean of the normal baseline distributions, which is set as Poisson distribution, while sigmab gives a variance matrix of the normal baseline distributions.
Priors, similar to the parametric method, need to be set for the Bayesian semiparametric method. As semiparametric method has more parameters than parametric methods, more priors need to be set. Thus, it is important to know what the characteristics of some of the prior distributions are:
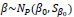 |
(7) |
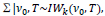 |
(8) |
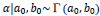 |
(9) |
where Γ and IW are Gamma and inverted Wishart distributions, respectively, or the conjugate prior for the covariance matrix of the multivariate normal distribution, respectively. a0, b0 provide the hyperparameters for gamma distribution. β0 and Sβ0 are calculated as coefficients of fixed effects, and could be calculated from the variance-covariance matrix of a fitted model by generalized linear mixed model, with penalized Quasi-likelihood; also α0 and b0, V0 and T were set as 1,1,3 and I, respectively [7].
The coefficients of βs are given independent non-informative or vague priors of N (0,Sβ0 = 1000). Alpha is a precision parameter highlighting the prior concentration for G (.) related to DP [26]. Alpha, the precision parameter was set as 10 to allow a moderate deviation from a Poisson family [8].
An analysis was conducted with the help of the Bayesian semiparametric generalized linear mixed model [7]. Both fixed and random effects could be specified in the syntax of the model. The random effects could be set for specifying a grouping or hierarchical level of the model, being set for traffic barrier types. The number of burn-in scans, the thinning interval, and the number of total scans to be saved were set as 5000, 19, and 5000, respectively.
2.2. Bayesian Hierarchical Modeling
As the semiparametric model used grouping variables in its modelling process, the hierarchical modelling, with various distributions, was identified as the closest model for comparison. Two hierarchal count models with Poisson and Negative binomial distributions were compared with the semiparametric approach.
These regression models are generalized linear models (GLM) with log as a canonical link function. The Poisson uses a log link with E[yi|Xi] = λi, which is the conditional mean, and the linear predictor µi as follows:
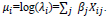 |
(10) |
For the negative binomial, the distribution of this model could be defined with two parameters p and r. To account for non-normal distribution of the Negative binomial, the overdispersion parameter of r is considered. Where the former, p, is referred to a success parameter, and for observation i defined as:
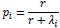 |
(11) |
The results of the analyses could be converted into an equation as follows:
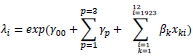 |
(12) |
In the above equation γ00 Is the population intercept averaged across various levels of barrier types, p is levels of traffic barriers, varies from 1 for box-beam to 3 as a w-beam barrier. γip is related to barrier intercept, based on various barrier levels. βks are the coefficients varying from 1 to 12. xki is the vector of observations related to kth coefficient being considered, and i is an observation number. It should be noted that the same equation is used for both negative binomial and Poisson models, and the estimated coefficient varies based on different considered distributions.
The non-informative priors with multivariate Normal prior with a mean of zero and very high variance were considered for all predictors for the two parametric models. As precision needs to be specified in the syntax of the model, this value is specified as
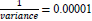
The choice of non-informative prior distribution for a variance parameter could have a big impact on inference, especially in problems where the number of groups is small [26]. Inverse-gamma has been used for the unknown variance of a normal distribution for non-informative prior [27]. Weak non-informative inverse-gamma was used for variance as p(σα2)~inverse - gamma (0.001,0.001) [28]. For over dispersion parameter, r, a uniform prior was used with an upper bound of 50.
Draws were attained from 3 MCMC chains, each consisting of 15,000 draws, where the first 5,000 were burned or discarded. The mixing of the chains was assessed, and then the draws were combined for a total of 30,000. Also, the 95% percentile interval was obtained from these draws. Model terms were assessed using percentile or credible intervals. Posterior summaries involve the mean, standard deviation.
It is worth emphasizing that the benefit of hierarchical Bayesian inference is that it does not focus on providing an independent estimator on each subset but considers the dataset as a whole. “Just Another Gibbs Sampler” (JAGS) package in R was used for the Bayesian hierarchical model using MCMC [29].
2.3. Data
Information from various sources was aggregated to build the dataset. Crash data, including various crash features, such as vehicles and drivers’ characteristics, were collected from the Wyoming Department of Transportation (WYDOT). As this dataset did not include roadside geometric characteristics, so data are collected and aggregated to traffic barrier data from the information related to more than a million feet of traffic barrier. That dataset contains information related to barrier length, height, and offset. The Wyoming roads map is presented in Fig. (2) to provide a summary of the road sketch in the state.
Crashes were filtered and aggregated to a barrier dataset based on road IDs and roadway mileposts. Only a single vehicle involved in barrier crashes was included in the dataset as there are expected many confounding factors in case of multiple vehicle crashes. Crashes were incorporated in the analysis if only they occurred between 2007 and 2017. That timeframe consideration is due to the lack of availability of a more recent dataset. The continuous predictor of the average annual daily traffic (AADT), length of barriers, and highway classifications were incorporated into the analysis to account for the exposure.
In total, the dataset included 1,923 barriers with a total of 18,502 EPDO crashes, where the majority of barriers are related to boxing beam barriers. The included predictors in Table 1 underwent a primary screening, and the identified predictors were found to be significant at least in one of the included models. The EPDO is calculated based on the WYDOT as the following equation: The shoulder width is transformed to a categorical format based on a width that divides this predictor into almost two equal categories.
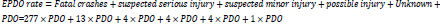 |
(13) |
As can be seen from Table 1, the data response is very sparse, with a wide variance and a large gap between a minimum value of one and a maximum of 555.
3. RESULTS
In order to identify the best-performed model in analyzing crash EPDO, DIC was used for comparing various Bayesian models. Similar structures with similar predictors were incorporated in all models. First, this section goes over the Bayesian semiparametric method and then discusses the two Bayesian hierarchical techniques.
3.1. Bayesian Semiparametric Method
For modelling EPDO based on a semiparametric Bayesian model, it was found that all the predictors are essential in predicting the EPDO crashes see Table 2. As mentioned earlier, it should be emphasized that the included predictors have already undergone a primary screening.
Here the random effect, or grouping variable, was set as the barrier types. The results show 95% highest posterior density (HPD) interval using the MCMC technique [30]. The results are primarily intuitive and expected. Speed involvement, improper restrain, and alcohol involvement all are associated with higher EPDO. As for the environmental conditions, the results indicated that in less-than-optimal conditions, dark and non-clear weather conditions, the likelihood of higher EPDO decreases compared with optimal conditions. Higher AADT and higher barrier length are associated with higher EPDO due to higher exposure.
| Variable Names | Mean | Variance | Min | Max |
|---|---|---|---|---|
| Response: EPDO | 9.6 | 37.383 | 1 | 555 |
| Barrier types;1*:box-beam,2:concrete,3:W-beam Box beam: 1,269 (66%), concrete=75 (4%), W-beam=579 (30%) |
1.6 | 0.916 | 1 | 3 |
| Gender: male * versus female | 0.3 | 0.395 | 0 | 1 |
| Speed involvement: speeding was exceeded the posted speed limit, versus speed was within the recommended speed * | 0.5 | 0.419 | 0 | 1 |
| Weather condition: clear* (vs. others) | 0.5 | 0.424 | 0 | 1 |
| Barrier height, in inch | 30 | 3.106 | 20 | 54 |
| Shoulder width greater than 5.5 ft* (vs. others) | 0.4 | 0.494 | 0 | 1 |
| Lighting condition: light* (vs. dark) | 0.4 | 0.413 | 0 | 1 |
| AADT | 2,468 | 1,646 | 27 | 8,853 |
| Length, in ft | 761 | 1490.201 | 14.396 | 35,471 |
| highway classification, non-interstate system* (vs. highway) | 0.5 | 0.497 | 0 | 1 |
| Mean | SD | HPD, Lower | HPD, Upper | |
|---|---|---|---|---|
| (Intercept) | 1.37 | 0.416 | 0.547 | 2.2 |
| Restrain conditions | 1.13 | 0.0202 | 1.09 | 1.17 |
| Gender | -0.2 | 0.021 | -0.309 | -0.226 |
| Speed involvement | 0.2 | 0.0195 | 0.121 | 0.196 |
| Weather condition | -0.5 | 0.0204 | -0.636 | -0.556 |
| Barrier height | 0.4 | 0.035 | 0.353 | 0.49 |
| Shoulder width | -0.5 | 0.135 | -0.794 | -0.264 |
| Alcohol involvement, no alcohol involvement* | 0.9 | 0.025 | 0.895 | 0.993 |
| Lighting condition | -0.3 | 0.0197 | -0.334 | -0.257 |
| AADT, continuous | 7E-05 | 5.35E-06 | 6.39E-05 | 8.47E-05 |
| Length of barrier, continuous | 0.11 | 1.43E-06 | 1.07E-04 | 1.13E-04 |
| Highway classification | -0.35 | 0.0207 | -0.391 | -0.31 |
| Barrier height × shoulder width | 0.13 | 0.053 | 0.0181 | 0.227 |
| Baseline distribution | ||||
| muB | 1.3 | 0.641 | 0.0756 | 2.620 |
| SigmaB | 0.4 | 0.606 | 0.053 | 1.1603 |
| Model's performance: Dhat=52097.06, pD=15, DIC=52,127 | ||||
It is also found that the impact of shoulder width and barrier height on EPDO should not be separated but considered an interaction term between these two predictors. This model's goodness of fit parameter is presented at the bottom of Table 2. In addition, the estimates of the baseline distribution are presented in Table 2. It should be noted that the mean of baseline distribution corresponds to the intercept mean of the model. Dbar is the posterior mean of deviance, while Dhat is the point estimate of the deviance. pD is the effective number of parameters, which is estimated by Dbar-Dhat, and DIC is the Deviance Information Criterion, which could be written as Dbar + pD or Dhat + 2 pD.
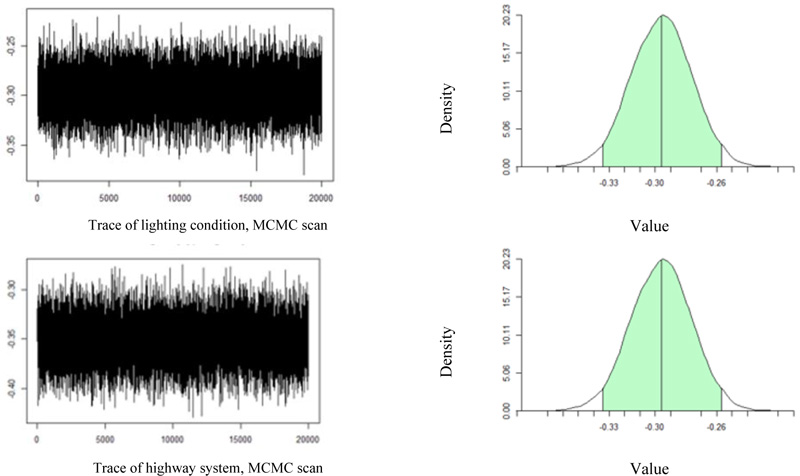
To evaluate the performance of the Metropolis Hasting (M-H) algorithm and to gain an insight into how the results in Table 2 are obtained, the trace plot and density of two predictors, as an example, are provided in Fig. (3). The Trace plot is an essential tool for assessing the mixing of a chain. The convergence could be confirmed if the plot does not stay in the same state for too long and when there are not too many consecutive steps in one direction.
The trace plot indicated that the chain is stable from each predictor resulting from MCMC. The plots on the right are the 95% HPD regions in the density plot and the posterior mean. The plots are based on generated posterior semiparametric using Dirichlet process mixture of normal priors for the random effects distribution. The density is estimated by employing DPM-mixtures models [24]. For instance, the posterior mean (95% HPD interval) for the lighting condition is -0.30, matching the value in Table 2. The same explanation would apply to highway classification, the bottom figures.
3.2. Bayesian Hierarchical Technique
Two Bayesian hierarchical models were conducted to be compared with the Bayesian semiparametric method and to find the best technique for modelling EPDO crashes. As the Poisson model is often considered a base model for conducting a count model, it is also considered in the comparison process.
3.3. Bayesian Hierarchical Poisson Model
The results of the Bayesian hierarchical model with a distribution of Poisson are presented in Table 3. Although many similarities can be observed between Bayesian semiparametric and Poisson models in terms of signs of the coefficients, the magnitudes of the coefficients vary across these two models.
The deviance of the model is presented at the bottom of Table 3. The DIC value is greatly increased by implementing the Poisson hierarchical model, 54,842 versus 52,127 for the semiparametric model. This is expected as the Poisson model does not accommodate the overdispersion or the more significant variance compared with the mean values. However, the equal mean and variance relationship could be relaxed for semiparametric, resulting in a better fit.
3.4. Bayesian Hierarchical Negative Binomial Model
While for Poisson distribution, mean and variance are equal, for negative binomial, variance is a quadratic function of the mean. This model was primarily conducted with the Bayesian semiparametric method to see which model could better accommodate the overdispersion. The directions of the coefficient of this model are in line with Poisson and the semiparametric method. However, the significance and magnitudes of the coefficients have been changed while moving to a more flexible modelling distribution.
As can be seen from the presented results in Table 4, while the impacts of coefficients of gender, speed involvement, and interaction of shoulder width and barrier height were identified as significant in Poisson and semiparametric methods, the impacts of these predictors on EPDO are found to be not crucial for the negative binomial model. Although the DIC of semiparametric was highly lower for the semiparametric model compared with the Bayesian Poisson model, this value is significantly lowered by implementing the negative binomial model, 11,513 and 52,127 for the negative binomial and semiparametric model, respectively.
| Mean | Std. Dev. | 2.50% | 97.50% | |
|---|---|---|---|---|
| Mean of random intercept (Barrier type mean) | 1.92 | 0.539 | 1.09 | 2.75 |
| Random intercept variance | 9.59 | 9.618 | 0.23 | 35.35 |
| Alpha [1]: box beam | 1.55 | 0.101 | 1.36 | 1.75 |
| Alpha [2]: concrete | 2.06 | 0.113 | 1.85 | 2.29 |
| Alpha [3]: W-beam | 2.14 | 0.105 | 1.95 | 2.35 |
| Restrain conditions | 1.09 | 0.020 | 1.05 | 1.13 |
| Length of barrier, continuous | 0.0003 | 0.00006 | 0.0002 | 0.005 |
| Highway classification | -0.32 | 0.020 | -0.36 | -0.28 |
| Barrier height × shoulder width | 0.57 | 0.057 | 0.46 | 0.68 |
| Gender | -0.26 | 0.020 | -0.30 | -0.22 |
| Speed involved | 0.13 | 0.019 | 0.09 | 0.17 |
| Weather condition | -0.63 | 0.020 | -0.67 | -0.60 |
| Barrier height | 0.32 | 0.036 | 0.25 | 0.39 |
| Shoulder width | -1.70 | 0.146 | -1.97 | -1.42 |
| Lighting condition | -0.31 | 0.019 | -0.35 | -0.28 |
| AADT, continuous | 0.0001 | 0.00004 | 0.00001 | 0.005 |
| Deviance | 54826.7 | 5.504 | 54820.1 | 54856.6 |
| DIC = 54841.9 pD = 15.1 |
||||
| Mean | Std. Dev. | 2.50% | 97.50% | |
|---|---|---|---|---|
| Mean of random intercept (Barrier type mean) | 2.03 | 0.486 | 1.19 | 2.86 |
| Random intercept variance | 54.73 | 99.339 | 0.93 | 262.82 |
| Alpha [1]: box beam | 1.89 | 0.34 | 1.21 | 2.54 |
| Alpha [2]: concrete | 2.04 | 0.403 | 1.24 | 2.83 |
| Alpha [3]: W-beam | 2.16 | 0.373 | 1.41 | 2.88 |
| Restrain conditions | 1.54 | 0.133 | 1.29 | 1.81 |
| Length of barrier | 0.0004 | 0.00008 | 0.0002 | 0.007 |
| Highway classification | -0.23 | 0.083 | -0.39 | -0.07 |
| Barrier height × shoulder width | 0.09 | 0.233 | -0.38 | 0.50 |
| Gender | -0.15 | 0.093 | -0.34 | 0.03 |
| Speed involvement | 0.14 | 0.084 | -0.03 | 0.30 |
| Weather condition | -0.93 | 0.083 | -1.10 | -0.77 |
| Barrier height | 0.09 | 0.118 | -0.13 | 0.33 |
| Shoulder width | -0.44 | 0.584 | -1.50 | 0.72 |
| Lighting condition | -0.29 | 0.088 | -0.46 | -0.11 |
| AADT, continuous | 0.0002 | 0.00005 | 0.00002 | 0.006 |
| Deviance | 11513.0 | 5.792 | 11503.73 | 11526.13 |
| DIC = 11529.7 pD = 16.7 |
||||
In summary, it was found that being unrestrained, driving in an interstate system, driving in clear weather, light conditions, and driving in higher traffic all increase the likelihood of EPDO crashes. The interaction for specific shoulder width and barrier heights was also found to be not significant.
As discussed, not accounting for overdispersion would result in an inaccurate estimation of the models’ results variability and underestimation of the estimated parameter variance. This can be observed by comparing the two-model standard deviation. For instance, all negative binomial variables resulted in a higher standard deviation compared with the Poisson model. Also, as can be seen from the two models, NB model penalizes more (higher pD) due to increased model complexity.
Finally, it should be noted that the criteria to keep variables were their certainty in the semiparametric model. So, this way, we work in favor of the semiparametric technique. For instance, while there are lower confidence intervals (CI) for gender for the semiparametric and Bayesian hierarchical Poisson model, there is a wide confidence interval (CI), including zero, for the Bayesian Hierarchical model. Despite that, the negative binomial model still outperforms the other considered techniques.
4. DISCUSSION
In the generalized linear model, it is assumed a linear relationship between the log of the expected response and other predictors. However, in crash data analysis, the assumption of linearity is often violated. This paper used a Bayesian semiparametric model in the context of a Poisson model to estimate a relationship between the number of traffic barrier EPDO and various explanatory variables. In addition, this model is compared with two Bayesian hierarchical models, Poisson and negative binomial distributions.
One fundamental interest of applying the Bayesian semiparametric model is the relaxation of parametric assumptions to gain modelling flexibility and robustness against unnecessarily misspecifications assumptions. The nonparametric technique allows nonlinear relationships to be accounted for, while it cannot be considered in a classical linear model. This method implements a partition of the sample space, where the distribution of each partition is the Dirichlet distribution with various hyper parameters.
The question might arise for the semiparametric model: how good is this model for accommodating over dispersed data. The answer to this question varies based on the complexity of the model, the number of included predictors, and the structure of the model. That point is essential for traffic safety studies as most crash count datasets are over-dispersed. The DIC measures use expected out-of-sample predictive error while penalizing the number of included predictors for a fair comparison across various models.
Another challenge of the included counts crash dataset is heterogeneity resulting from the dataset's structure: observations belonging to a specific traffic barrier type are not independent. This is where hierarchical modelling plays a role by compensating the bias by considering the dependence between various observations. Bayesian hierarchical modelling was identified as closest model to the structure of the Bayesian semiparametric method. In the Bayesian semiparametric model accounting for hierarchy could be achieved by setting a grouping as various barrier types, while in Bayesian hierarchy, it could be specified by setting a different intercept for barrier types.
DIC method was used as a sole model assessment method due to the limitation of other measures such as the Bayes factor. DIC was substantially reduced from BHP to semiparametric and from semiparametric to HNB. Although the obtained results of the three models are in line, in terms of signs, for all methods, the significance of the predictors varies, especially across the Hierarchical model with negative binomial distribution and the two other models.
The better fit of the HNB was despite the fact that we based the inclusion of variables on the semiparametric technique. For instance, many variables such as gender, which were significant in the semiparametric method, were not in the HNB model. Another essential comparison being made across the models was estimated parameters' variance. As discussed, not accounting for overdispersion results in underestimating the variances of the parameter and consequently biased point estimates. This could be observed by comparing the two-model standard deviation.
It should be highlighted that the results are specific to the dataset used in this study, and more studies are needed to confirm the results. More flexibility could be given to the semiparametric technique by setting other based distributions in future studies so the results could be more comparable with the negative binomial distribution.
CONCLUSION
As this study is a starting point for conducting a cost-benefit analysis of barriers in the state, and the variables of barrier heights and shoulder-width were found to be of crucial importance, other ranges of these two predictors need to be considered for future studies. This is because the interaction between these two predictors was found to be not crucial for a finalist model, or HNB. This study can serve as a guideline for future studies for implementing suitable distribution.
LIST OF ABBREVIATIONS
| DIC | = Deviance Information Criterion |
| NB | = Negative Binomial |
| ROTR | = Run-off-the-road |
| EPDO | = Equivalent Property Damage Only |
| HNB | = Hierarchical Negative Binomial |
| DP | = Dirichlet Process |
| CI | = Confidence Intervals |
CONSENT FOR PUBLICATION
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
Mahdi Rezapour is the Associate Editorial Board Member of The Open Transportation Journal.
ACKNOWLEDGEMENTS
Declared none.


