All published articles of this journal are available on ScienceDirect.
A Simulation Model to Determine the Capacity of a Y-Type Waterway Intersection for a Real Seaport
Abstract
Introduction:
In this paper, Arena software has been used to simulate a complex system, which contains traffic rules, a tidal window, weather conditions and different fleet types.
Methods:
We have determined the capacity of a Y-type waterway intersection with a sailing speed of 10 knots for the Panjin seaport in China. Moreover, we chose a sailing speed of 11 knots, which gives a safe squat value at high tide level whose cumulative frequency for channel accessibility is larger than or equal to 80%.
Results:
The results show that the capacity of the waterway reduced with a sailing speed of 11 knots, because of waiting for a long time to meet a high tide level.
1. INTRODUCTION
With the increase in the number of vessels arriving at port and increases in the length of the navigational channel, the sailing time increases especially for the very long one-way traffic channel. As a result, it will increase the total time spent in the port. ATAT (average turnaround time) is a ship time in the port which includes the waiting time (waiting time includes a ship’s waiting time for berth availability and channel availability), handling time, and berth service time [1]. Some port operating conditions such as the safe distance between sailing ships has an effect on the channel capacity. Many ports use the safe distance of 3 ~ 6 times the vessel length between vessels [2]. For instance, as Tianjin port considers the safe distance as six times the vessel length at least, Yangtze Estuary Deepwater Channel requires that the time intervals between ships which sail in the channel are six minutes at least [3].
In this paper, there was no liquid natural gas ship (LNG), since liquid natural gas (LNG) ships need more security zones [4]. According to the length of the longest ship arriving at the port, the safe distance is between 3-6 L. Therefore, ten minutes were chosen as the safe time between arrival and departure vessels (safe time between ships in convoy).
Not all the ports operate all the days of the week, as some ports do not operate during weekends. As concerns, the channel opening hours, some channels are accessible at all hours and others may be only accessible during the day [2]. In this paper, it is considered that the port operating days include all seven days in the week and the access channel is available 24 hours per day.
Some port operation days are restricted because of bad weather conditions, although this reason cannot be changed because it is for a limited number of days per year. One of the factors that affect the channel capacity is the vessel speed, as it is confined to increase the ship velocity inside the harbor, because it is hard for tugs to make fast [2]. It may be acceptable for the ship to use its maximum cruise speed to sail in the outer channel. But firstly, one must check the squat to know the acceptable high speed to be used in the outer channel, and the ship will reduce its speed gradually to the current speed in the harbor (3~4 Knots).
In our case study, we chose the ship sailing speed of 10 knots. When we designed the channel depth, we took into account the facts affecting sinkage of the hull such as squat allowance, wave response allowance, possible error of chart datum, meteorological and oceanographic conditions, other environmental conditions, securing a safety benefit. As long as the ship was sailing on restricted water, it essentially needed to maintain enough (UKC) Under-Keel Clearance, which is the space between the ship’s bottom and the seabed to avoid the deterioration of maneuverability and bottom damage.
1.1. The Concept of the Squat
The moving ship hull’s backflow causes a steady downward displacement, including translation and rotation, which is termed as ‘squat’ [5]. The relative velocity between the surrounding water and the vessel will be influenced according to this water motion. As a result, it will cause a water level depression in which the vessel sinks, where these effects increase in case the vessel sails through shallow water or channel banks [5, 6].
1.2. The Causes of Sinkage and Trim
The velocity field creates a different hydrodynamic pressure along the ship, since potential and kinetic energy must be in equilibrium similar to Bernoulli influence [5, 7]. As a result, a downward vertical force and moment about the transverse axis lead to sinkage and trim, respectively [5, 6].
Indeed, the ship squat factor is the most important factor in the calculation of under keel clearance. To estimate the squat value, there are seven empirical formulas [5]; among them, there are four complex formulas which are Huuska/Guliev, Eryuzlu 2, Romisch and Tuck. The most common formula is the Huuska/Guliev, which was recommended in The Finnish Maritime Administration (FMA) and The Spanish Rom (2003) for all three channel type configurations. To use this formula, the depth Froude Number Fnh should be not greater than 0.7 [2, 5]. In this paper, we used this formula for calculating squat value.
1.3. The Froude Depth Number
This formula is used to control the hydrodynamic resistance of the ship during its movement in shallow water [2, 5, 6], where the dimensionless Fnh is presented in Equation. (1).
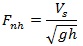 |
(1) |
(Vs is the ship speed (m s-1), h is the water depth (m), g is the acceleration due to gravity (m s-2)), if the ship velocity produces a large Froude Number, it suffers from hydrodynamic resistance to motion in shallow water, and as a result, the ship will consume additional power which will expand the energy existing in primary and secondary waves, thus, sailing with high speeds would be counterproductive [2, 5].
The Seaport Waterway Capacity is defined as:
The sum tonnage of all ships that are sailing through the channel per year under a certain port service level [3].
There is another definition according to PIANC guidelines which says “the maximum traffic volume can be handled under meeting the expectations and needs of the safety levels and the required service for the approach system.” [5].
1.4. Rockwell Arena
At present, the representative special simulation software available includes Rockwell Arena, ProModel, Witness and eM-Plant. Among them, Rockwell Arena is mainly used for discrete event system simulation, with the following powerful features:
• Practical Modeling Tools
Arena provides input data analysis tools, simulation optimization tools, process analysis tools, output analysis tools and 3D player tools for 3D visualization for modeling and simulation.
• Rich Modeling Templates and Modules
The simulation modeling tool is the main part of the arena simulation software, used for modeling convenience. Arena provides a large number of users direct use of the modeling template, and different templates can be used to build a large number of modules according to their different functions in the modeling, and can be divided into process modules and data modules.
• Process-Oriented Approach
Arena can establish a process for all entities which not only reflects the entity from the production to leave all the activities, but also to provide users with simulation events tracking. While using ARENA, different levels of templates or code can be used in one model at the same time [8].
Practice studies have shown that Rockwell Arena, as a universal visual interactive integrated simulation software, has a wide range of applications and covers virtually all areas of visual simulation, including manufacturing systems, public systems and service systems, especially where the service system is very extensive, such as traffic in the highway traffic control, container terminal logistics system simulation and optimization research, port transport planning model, vehicle scheduling and so on. Therefore, this study selected Rockwell Arena software as a simulation software technology support [9].
2. PROBLEM DESCRIPTION
Many published papers are focused on some of the terminals in the harbor, but not all of the port terminals [10]. In a realistic case, most of the ports consist of different terminals with different fleets as shown in Fig. (1) . In this paper, the focus is on simulating the traffic of a Y-type waterway intersection. The complex port access channel with the Y - intersection scheme and the movement of the vessel from arrival at the port to its destination berth in the harbor and vice versa have all been simulated. This paper presents a complex port simulation model that takes into account seven different fleets with various vessel loads and determines the turnaround time for each fleet, to be able to determine the port service level which is important for the owners of vessels, owners of imported goods and vessel operators [1].
This paper consists of two parts: the first part is “A simulation model to determine the capacity of the Y-type waterway intersection ”. In this part, we discussed the simulation model with details of the complex port access channel. The authors already have determined the capacity of the Y-type waterway intersection.
The second part of this paper was added to study additional matter related to the use of different tide cumulative frequencies to understand the relationship between the channel capacity at different ship speeds. So the authors only chose the eastern area to study this additional matter. In addition, there was another purpose: the author wanted to illustrate to the other researchers who will be reading this paper that the simulation model can be used to simulate the waterway with and without a waterway intersection for studying the channel capacity with various sailing speeds. If we chose the main channel and eastern branch navigation channel or the main channel and western branch navigation channel or the Y-type waterway intersection, the aim will be the same; that is, to understand the relationship between the channel capacity at different ship speeds while taking into account different cumulative frequencies for the tidal level.
3. METHODOLOGY
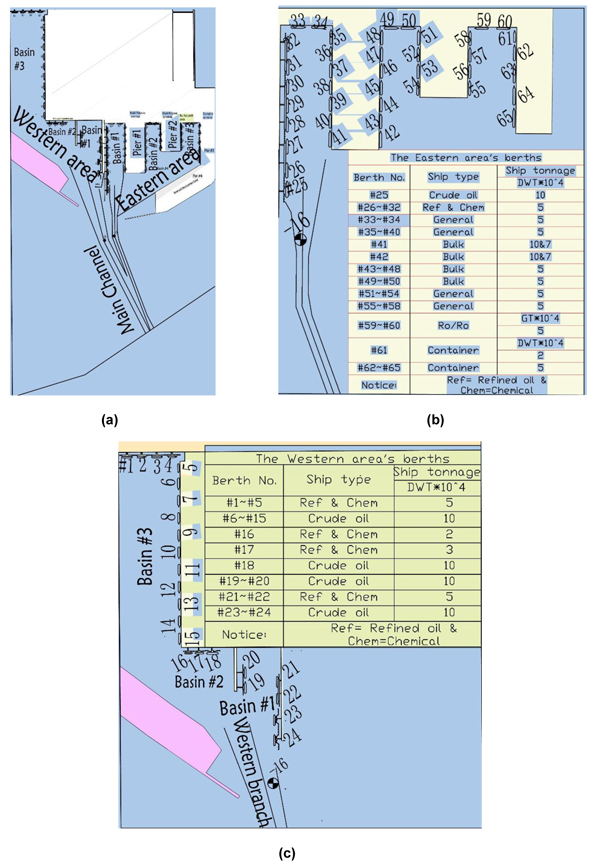
In this paper, the channel traffic type was one-way traffic, the logical model for an inbound ship (ship sailing towards the port) as shown in Fig. (2) , is the same logical model for the outbound ship (ship sailing towards the sea) except for the need to check berth availability for berth allocation procedures.
3.1. Model Assumptions
- A ship is sailing in a one -way traffic navigation channel
- The channel is straight; there are no bends
- After the ship arrived, if the weather is bad, it would wait and would not leave the port until its services are carried out completely
- The traffic rule is first come, first serve (FCFS)
- Loading/unloading and other berth operation times are taken as part of berth service time
- The model does not consider the movement of ships within the Anchorage area and it does not consider the active status of cranes and storage yards
3.2. Logic Flowchart of Ship Operations for An Arrival Ship With a Y-Type Waterway Intersection
Indeed, channels should use traffic flow simulation models to estimate the capacity of port navigation [5]. Because the traffic system of the approach system is complex, most of the ports all over the world have different terminals in a harbor with various fleet types, and each fleet has different arrival times due to the stochastic operations in the port, which need to deal with different ship types, with various service levels, tidal windows and other traffic rules. In this paper, Arena simulation has been used to simulate a complex port access channel network based on the above flow chart of the logical model and the assumptions to simplify a complex port network, in order to study the navigation channel capacity under various operating conditions.
4. SIMULATION MODEL
4.1. Input Parameters
The input parameters include ship parameters, channel traffic type, entry and exit rules for the port, berth tonnage composition, natural conditions, and the tidal window.
4.1.1. Ship Parameters
Our case study port, Panjin port, is equipped to receive seven different fleet types and each fleet has different ship tonnage and size. The ship tonnage composition was collected by the port authority according to statistical data. A negative exponential distribution was chosen to simulate the time interval for arrival between two successive ships from the same fleet [1, 2, 5, 10-12].
4.1.2. Channel Traffic Type and Entry& Exit Rules for the Port as Input Parameters
In this paper, we only considered a one-way traffic navigation channel, and therefore, no overtaking is permitted. Some ports give priority for the large ships which need the tidal level to enter or exit the channel, while other ports give high priority to the container ships with different tonnages [2]. There are other traffic rules such as (FCFS) First Come, First Serve and a high-priority traffic rule for the outbound ship, with the latter being known as Leaving Port Priority [11]. In this paper, we have chosen the FCFS rule.
4.1.3. Berth Tonnage Composition and the Berth’s Service Time
Suitable for shiploads that reach the port. Each shipload has a berth service time, which is estimated by the port authority’s experience and collected historical data. In the simulation model, we used an exponential distribution with a mean berth service time to simulate the berth service time [1, 12].
4.1.4. Natural Conditions
Natural conditions limit the number of port operating days. These natural conditions include wind, fog, rainfall, waves and so on. Ships may sail slowly or even stop sailing during occurences of snow, fog and storms, severely affecting the waterway traffic, and in windy weather or typhoons, ship speed and traffic safety are also adversely affected. When the wave height is greater than the design value in the waterway and harbor area, the loading and unloading operation will not be carried out [13]. One of the most important factors in the simulation model is port operating days in a year.
Due to the differences in meteorological conditions of each port area, it is difficult to get a unified distribution law. Since the purpose of this paper’s case study is to calculate the capacity of the navigation channel, in the simulation model we assumed that, after the ship arrives, if the weather is bad, it would wait in the Anchorage area and will not leave the port until it finishes its service. The total adverse weather days in our case study are 77 days/year. Therefore, 77 days/year are uniformly distributed through the period of one year in the simulation model as non-operational days [1, 12, 14].
4.1.5. Tidal Window
Due to the natural conditions of the port or in an effort to reduce dredging costs, most ports use the tidal window for large ships to allow passage through the channel during a limited duration of the tide, thus, the tidal window has become an important element affecting navigation. In this paper, we have used the tidal level which corresponds to 90% cumulative frequency for a limit of the tide duration equal to 3.5 hours, as illustrated in Table 1.
| Tidal Duration (hours) | Tide Cumulative Frequency | |
|---|---|---|
| 80% | 90% | |
| 3.5 | 1.93 | 1.74 |
4.2. Model Establishment
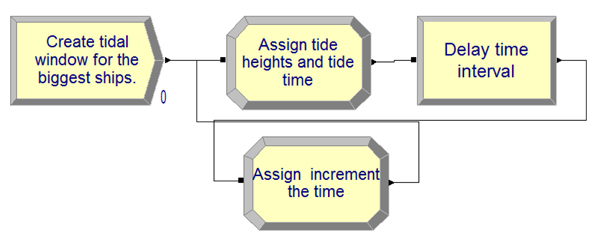
To simulate the tidal window in the Arena simulation model, we used a variable to simulate the daily tidal level per hour over 365 days of one year of Port operations. Moreover, we generated a sub model as shown in Fig. (3), using “assign modules” to define variables for the tide level and its corresponding time. Moreover, other “assignments” for calculating the tidal level and tide period were considered. If the ship needs a tidal window to sail through the channel to its allocated berth, as an inbound ship it can use this sub model to calculate the current continuous tidal duration with the high tide window. Once it has met enough tide window and traffic conditions, the ship sails through the channel to its allocated berth to begin the handling operation at berth. An outbound ship will do the same checks, the only difference being the revised direction of the movement.
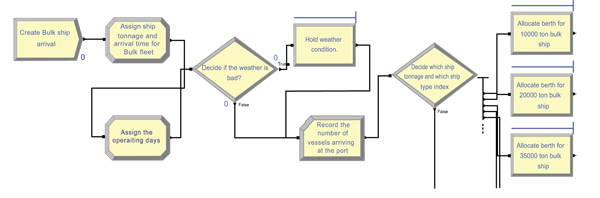
The different fleets for our case study for the eastern area of Panjin port in China, are Container, General, Bulk, Chemical, Refined oil, Ro/Ro and Crude oil fleets. Each fleet has different ship tonnage. To simulate the arrival process for each fleet type, we generated a “Create module” to define the time between two successive arrivals (the inter-arrival time between ships for the same fleet), by using negative exponential distribution. Using the discrete function to define different ship tonnage for the same fleet, as an example, we will take a bulk fleet type to illustrate how to use the discrete function. Firstly, one “create module” is used to represent the ship arrival for this fleet type. To distinguish between different ship tonnages for the same fleet, an “assign module” was used to define an attribute called ship tonnage, which is illustrated in Table 2. Inside this “assign module,” we used a discrete function which is described in the Arena by this formula: DISC (Cumulative probabilities, and values), so with using the Table 2 values we got DISC(0.13,1,0.34,2,0.61,3.5,0.97,5,0.99,7,1,10). At the same “assign module” we have defined an attribute for the ship type index, which will be used to follow the path of this fleet anywhere within the model and another attribute to record the arrival time for each ship.
| Ship Tonnage (ton) | 10000 | 20000 | 35000 | 50000 | 70000 | 100000 |
|---|---|---|---|---|---|---|
| No.of ships (ship) | 144 | 232 | 299 | 399 | 22 | 11 |
We used the “Decide module” to determine weather conditions. According to the port weather condition data which was simulated by using “Assign module” to define a discrete function (DISC (0.211,0,1,1)), “0” indicates inclement weather with a probability of 0.211, and “1” indicates good weather, as shown in Fig. (4).
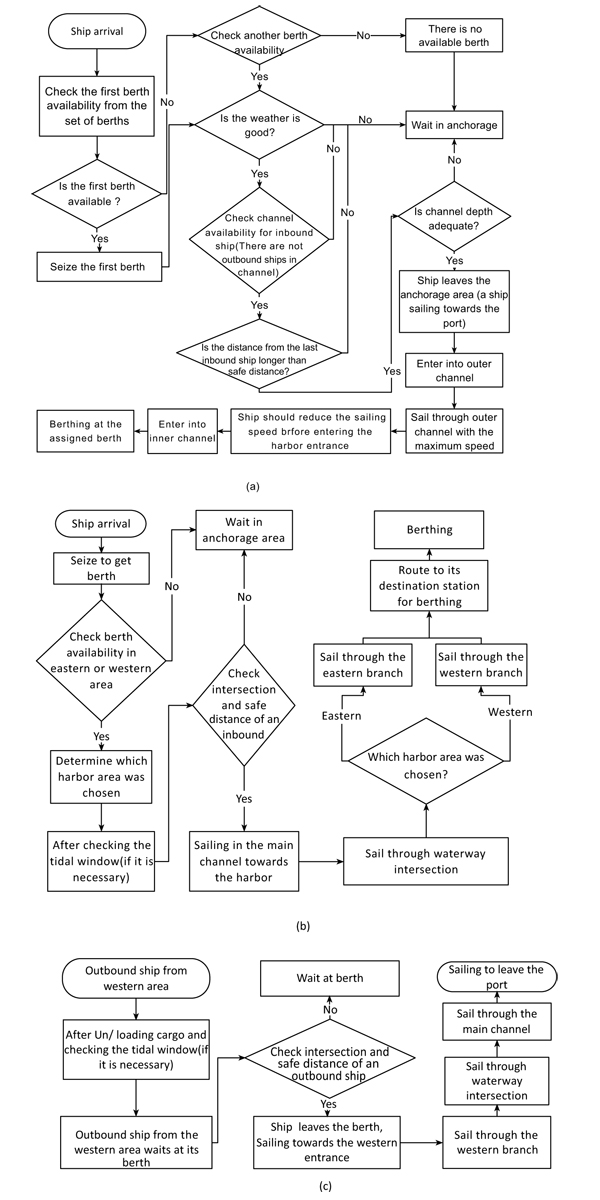
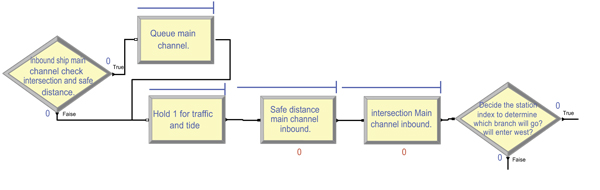
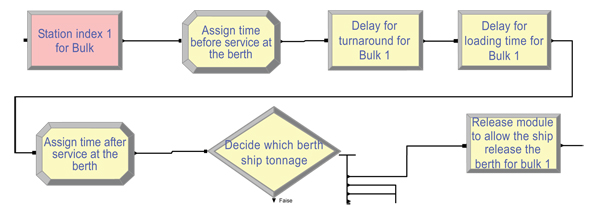
For inbound ships, after the ship seizes a berth and meets weather conditions and the tidal window for the biggest ships, safety for sailing through the channel must be checked, and one must ensure there is no outbound ship in the main channel or eastern and western branches, and ensure that the security time between it and the previous ship is 10 minutes. Then it can sail through the main channel and enter the eastern or western branch. The author states some conditions by using work in process (WIP) in the “process modules” to check the traffic rules, similar to the highways [9]. If the check intersection and safe distance conditions are not safe, the ship will wait in the Anchorage area, using “hold module” for the ship to preserve its place in the queue until channel accessibility, as shown in Fig. (5), using “Route” and “Station” modules to guide the ship to its destination station. Then “delay modules” are used to simulate handling time at the berth, as illustrated in Fig. (6). After completing the loading and unloading of the ship, an outbound ship will wait to use the channel, checking the tidal window (if it is necessary) and traffic conditions.
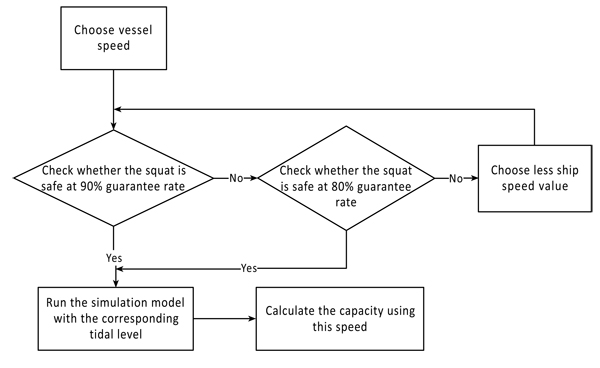
In the second part of this paper, we have only chosen the eastern area navigation channel with their different fleet types to study the channel capacity with various sailing speeds of 8, 9, 10 and 11 knots, and the squat ship calculations having been done. Then, by using the logic flow chart illustrated in Fig. (7), we simulated the ship sailing through a very long one-way approach channel at different speeds to its destination berth in the harbor, for inbound and outbound vessels. We have taken into account the safe distance between ships, weather conditions, traffic conditions and the tidal window for a larger ship tonnage.
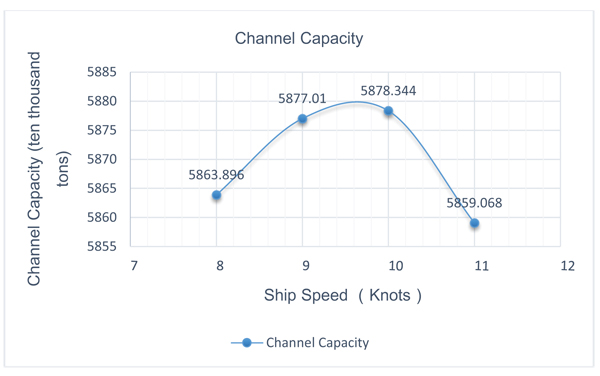
After running the simulation model for one year, we have calculated the capacity of the channel by using ship sailing speeds equal to 8, 9, 10 and 11 knots as shown in Fig. (8).
5. RUN LENGTH AND NUMBER OF REPLICATIONS
Arena simulation software has two-time-frames of simulations which are terminating and steady state. In a terminating simulation, the assumption is that the model starts empty and idle, where empty means there are no entities presented at time zero, and idle means all resources are idle at time zero [8]. However, the real case of the port is that it has vessels in the harbor, and the resources are not idle. Therefore, we must choose the steady state, which means that after the warm-up period overs, the system will reach the steady state at that moment. Then the arena will clear all of the statistics for the warm-up period and will start the statistic collection after the warm-up period is over [8, 9]. By using this Arena method, we got the value of the warm-up period of about 30 days.
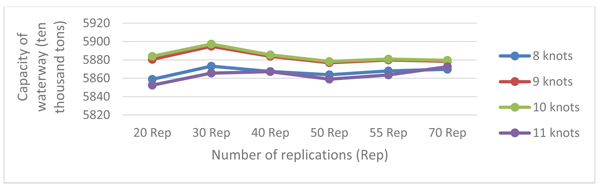
After making more replications, we can perform some additional analysis that would allow us to make some useful interpretations of the output. Estimating a sufficient number of replications requires more computational effort by the modeler [1, 12].
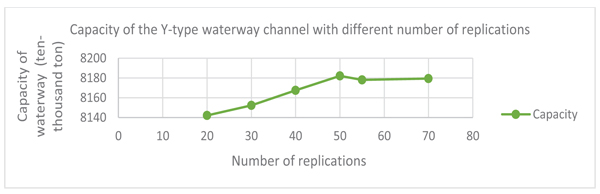
In this paper, we considered different sailing speeds which are 8, 9, 10 and 11 knots to estimate the corresponding channel capacity value (Fig. 9) illustrates the variation of the channel capacity over the number of repetition times with different ship sailing speeds, and we can notice that the change in channel capacity remained constant after 50 repetitions, so the sufficient amount of replications that are chosen for our case study is 50 repetitions.
6. VERIFICATION AND VALIDATION OF THE MODEL
In this paper, the author validated the simulation model by queuing theory and service time at berth evaluated by way of the port authority’s experience and the collected historical data.
In order to check the correct programming of inter-arrival distribution function NED used in our simulation model, we evaluated the expected number of ships per year. The correlation coefficient R2 between the simulated and theoretical results is equal to 0.9996. Hence, the modeling of the inter-arrival time is correct.
To validate the effectiveness and practicability of the simulation model, we need to compare the simulation results with real data.
Average service time is the ship’s average service time at berth. We validated the simulation model by comparison of its results with real average service time data, for example “General cargo ship”:
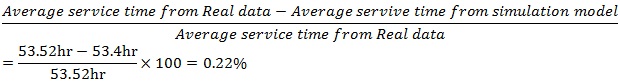 |
In the absence of real data, we can use the queuing theory to test the model, to be able to evaluate the model results. We got the correlation coefficient between the theoretical and model’s results as R2 =0.9886. Hence, the performance of the simulation model is correct.
7. RESULTS
Fig. (10) shows the results of the simulation model after running it for one year to determine the capacity of the seaport waterway, taking into account the Y-type waterway intersection. The simulation results of ATAT (average turnaround time) per fleet for the Y-type waterway intersection simulation model are: container =9.78 (Hours); Ro/Ro=12 (Hours); Refined oil = 20.06 (Hours); Chemical = 29.35 (Hours); General = 53.61 (Hours); Bulk = 16.077 (Hours) and Crude oil= 176.92( Hours).
According to PIANC [5], the results show the Container, Ro/Ro, Refined oil, Chemical, General, and Bulk fleets, have an acceptable total time spent in the port, though the total time spent on the crude oil fleet in the port is relatively long. This is because the ship tonnage considered in this paper for the crude oil ship is 100,000 tons, and it has a maximum fully loaded ship which needs to use the tidal window. Although we designed the channel according to high sailing speed value, the tidal window has an effect on the total time spent in the port for the crude oil fleet.
With regard to changing the ship speed value and its determined effectiveness on the channel capacity only for the main channel and eastern branch, Fig. (8) has shown that channel capacity increases with the increase in sailing speed. However, when using 11 knots at a higher tide level whose cumulative frequency for channel accessibility is equal to 80%, the capacity will be reduced.
As shown in Fig. (9) at 50 repetitions, we can notice that the maximum channel capacity corresponds to the ship speed value at 10 knots, then 9 knots, then 8 knots, and the lowest channel capacity value corresponds to 11 knots.
CONCLUSION
We built a traffic simulation model to simulate the real state of the access channel with a Y-type waterway intersection, taking into account the stochastic arrival process of different fleet types, weather conditions, and the tidal window as a navigation limit for larger vessels, and we simulated the ship movements from arrival at the port to its berth in the harbor. Moreover, we have illustrated an appropriate simulation model. In this research, the mentioned method can be applied to determine the channel capacity under different sailing speeds before applying them in reality.
After running our traffic flow simulation model for one year, we used it to determine the capacity of a complicated port system as a whole, taking into account the Y-type waterway intersection.
In the second part in this research, we calculated the maximum squat value allowable with a sailing speed of 10 knots. Sailing at a speed of more than 10 knots would give unsafe squat values, so we tried to use a higher tide level whose cumulative frequency for channel accessibility is equal to 80%, and recalculate the squat value with a sailing speed of 11 knots, and the empirical results showed that the squat would be safe with a sailing speed of 11 knots.
We chose the access channel for the eastern area and rebuilt the simulation model. After comparing the capacities of the waterway by using different ship speeds, we notice that when a ship sails at 10 knots, it will produce the maximum channel capacity, while sailing with 11 knots gives the lowest capacity value. This is because the larger ships will need to wait for a long time to meet the higher tide level whose cumulative frequency for channel accessibility is equal to 80%.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The authors wish to express their thanks to the National Natural Science Foundation of China (No. 51309049) for its financial support.


